Задача Расчет переходного процесса в линейной электрической цепи
 Скачать 199.77 Kb. Скачать 199.77 Kb.
|
|
Задача 1. Расчет переходного процесса в линейной электрической цепи Таблица 1 – Исходные данные
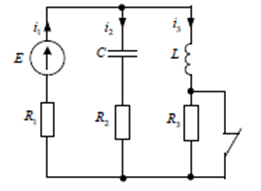 Рисунок 1 – Исходная схема Требуется: 1. Рассчитать переходный процесс классическим методом. 2. Рассчитать переходный процесс операторным методом. 3. Построить графики искомого тока или напряжения. 1 РАСЧЕТ КЛАССИЧЕСКИМ МЕТОДОМ Рассчитаем независимые начальные условия. Учтем, что при действии в цепи источника постоянной ЭДС индуктивность L имеет нулевое сопротивление (закоротка), а емкость представляет разрыв. Исходная схема для расчета 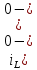 приведена на риснуке 2. приведена на риснуке 2.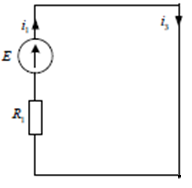 Рисунок 2 – Исходная схема для расчета начальных условий 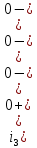 Найдем корни характеристического уравнения. Схема после коммутации имеет вид рисунок 3. 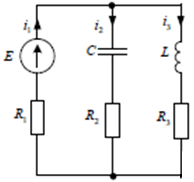 Рисунок 3 – Схема после коммутации Для получения характеристического уравнения рационально составить выражение входного сопротивления 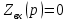 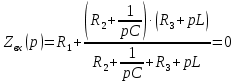 Подставив исходные данные получаем уравнение: 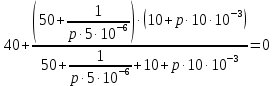 Данные уравнения целесообразно решать в программе Mathcad 14 с помощью команды Find 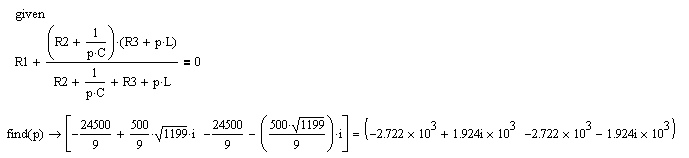 Корни уравнения равны: 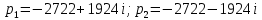 Запишем выражение для свободной составляющей тока 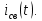 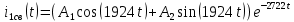 Где А 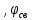 – постоянные интегрирования – постоянные интегрированияТаким образом, для тока 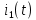 имеем имеем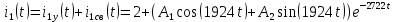 Где 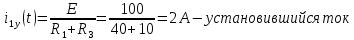 Определим зависимое начальное условие – значение производной 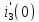 в момент коммутации. в момент коммутации.По первому и второму закону Кирхгофа: 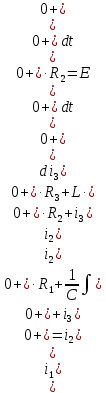 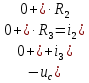 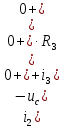 По первому закону кирхгофа: 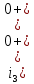 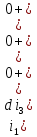 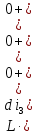 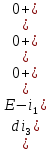 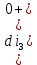 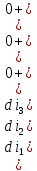 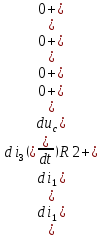 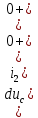 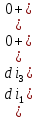 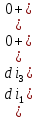 Определим постоянные интегрирования 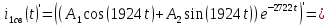 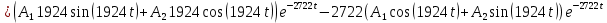 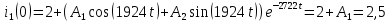 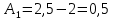 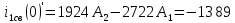 Решаем уравнение, и получаем 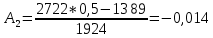 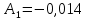 Окончательное уравнение тока i1(t) имеет вид: 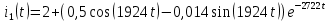 2 РАСЧЕТ ОПЕРАТОРНЫМ МЕТОДОМ 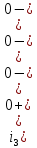 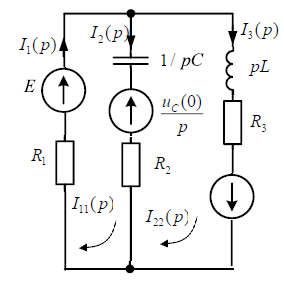 Рисунок 4 – Схема для расчета операторным методом По методу контурных токов: 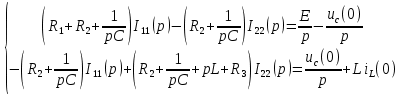 Рассчитаем контурные токи по методу Крамера в программе MathCad14: Найдем определитель 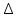 : :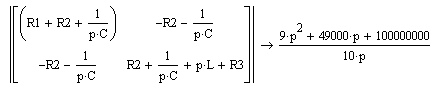 Найдем 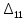 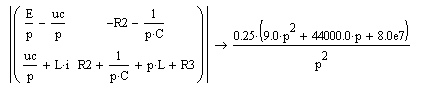 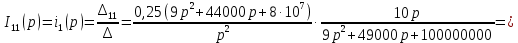 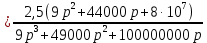 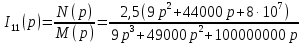 Определим корни уравнения 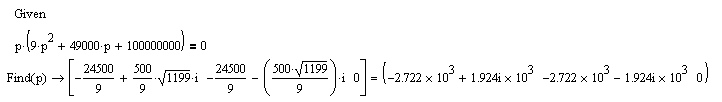 Корни уравнения равны: 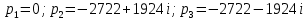 Производная знаменателя изображения тока равна: 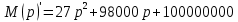 Установившийся ток равен: 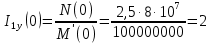 Найдем оригинал свободной составляющей: 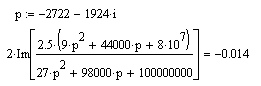 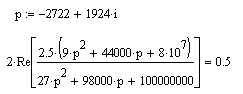 Окончательное уравнение тока i1(t) имеет вид: 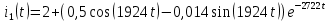 Построим график i1(t) 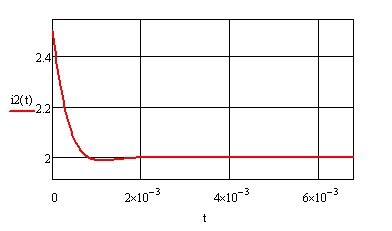 Рисунок 5 – График i1(t) Задача 2 Определить закон изменения во времени тока в одной из указанных ветвей схемы или напряжения на заданном участке схемы. Таблица 2 – Исходные данные
 Рисунок 6 – Исходная схема 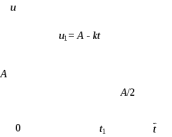 Рисунок 7 – Исходный график Решение: 1) определим переходную функцию по току 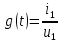 , при , при 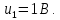 Классическим методом 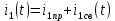 Где 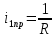 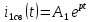 Определим методом входного сопротивления корень характеристического уравнения p: 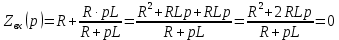 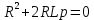 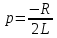 По законам коммутации: 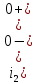 По первому закону Кирхгофа: 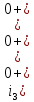 По второму закону Кирхгофа: 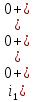 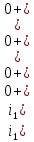 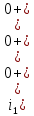 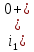 Подставляю полученное значение при t=0+ в уравнение для 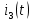 определим коэффициент A1: определим коэффициент A1: 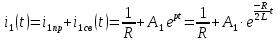 при t=0+ получим: 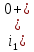 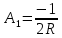 Тогда: 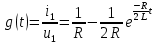 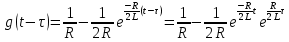 Определим реакцию цепи применяя интеграл Дюамеля на интервале: Времени 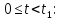 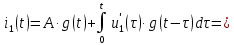 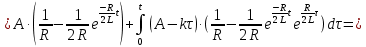 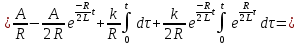 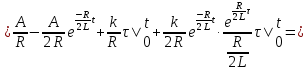 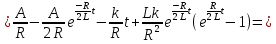 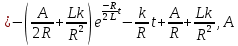 Определим реакцию цепи применяя интеграл Дюамеля на интервале Времени 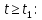 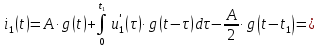 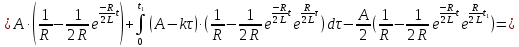 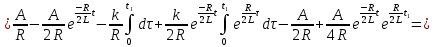 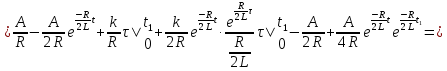 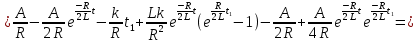 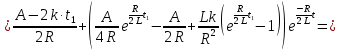 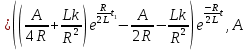 |
