математика. Исследование на экстремум. y 4x16x 2 Находим интервалы возрастания и убывания
 Скачать 75.14 Kb. Скачать 75.14 Kb.
|
|
Задание 1 Вычислить предел 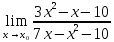 При 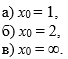 а)  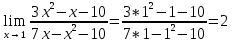 б)  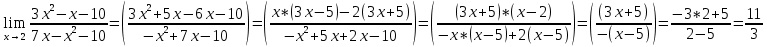 в)  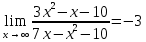 Задание № 2. Найти производные функций. 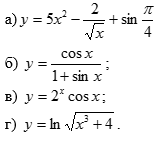 а) 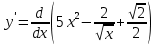 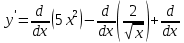 ( (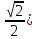 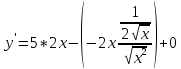 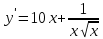 б) 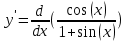 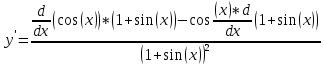 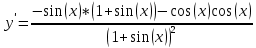 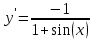 в) 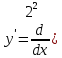 * *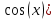 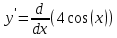 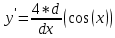 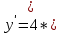 - -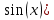 г) 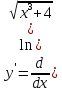 )) ))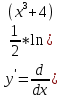 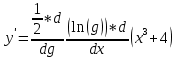 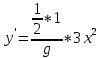 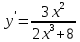 Задание № 3. Исследовать данную функцию методами дифференциального исчисления и построить ее график. 1) Область определения функции. Точки разрыва функции. 2) Четность или нечетность функции. Функция общего вида 3) Периодичность функции. 4) Точки пересечения кривой с осями координат. Пересечение с осью 0Y x=0, y=0 Пересечение с осью 0X y=0 5) Исследование на экстремум. y = 4*x/16+x^2 1. Находим интервалы возрастания и убывания. Первая производная Находим нули функции. Для этого приравниваем производную к нулю 8·x+1 = 0 Откуда: x1 = -1/8
В окрестности точки x = -1/8 производная функции меняет знак с (-) на (+). Следовательно, точка x = -1/8 - точка минимума. 2. Найдем интервалы выпуклости и вогнутости функции. Вторая производная. f''(x) = 2 Находим корни уравнения. Для этого полученную функцию приравняем к нулю. 2 = 0 Для данного уравнения корней нет. 6) Асимптоты кривой. Уравнения наклонных асимптот обычно ищут в виде y = kx + b. По определению асимптоты: Находим коэффициент k: Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. Задание № 4. Вычислить неопределенные интегралы. 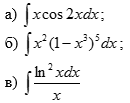 а) u=x dv= 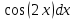 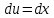 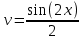 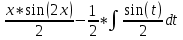 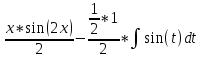 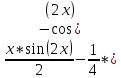 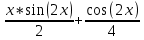 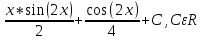 б) 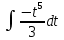 - 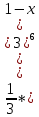 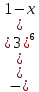 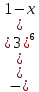 Задание № 5. Вычислить площадь фигуры, ограниченной линиями y=x2–4x+3 и y =x–1. Построить график. 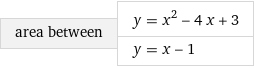 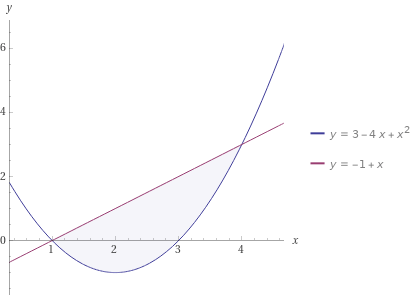 |
