дфи. Lab_rabota_3оту. Исследование областей устойчивости линейных систем с сосредоточенными и постоянными параметрами методом dразбиения
 Скачать 335.76 Kb. Скачать 335.76 Kb.
|
|
МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ (Национальный исследовательский университет) Кафедра 301 Дисциплина: «Основы теории управления» Отчет по лабораторной работе №3 Тема: «Исследование областей устойчивости линейных систем с сосредоточенными и постоянными параметрами методом D-разбиения» Выполнил: студент группы М30-305С-17 Малахов Данила Сергеевич Принял: Боголюбов Александр Александрович Москва, 2020 Цель работы Изучить метод исследования областей устойчивости линейных систем с сосредоточенными и постоянными параметрами в плоскости двух параметров. Постановка задачи Задана структурная схема исследуемой системы вида: 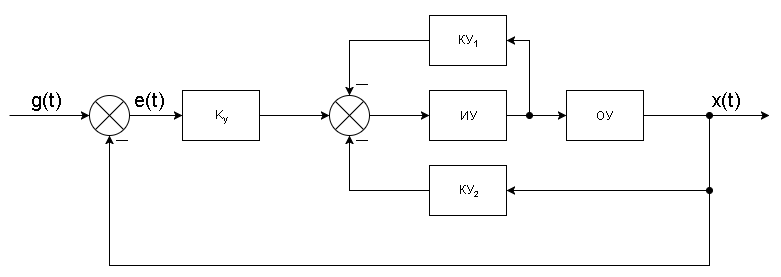 Где 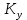 — усилитель с передаточной функцией — усилитель с передаточной функцией 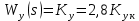 , ,ИУ — исполнительное устройство с передаточной функцией 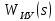 , ,ОУ — объект управления с передаточной функцией 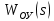 , ,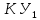 — первое корректирующее устройство с передаточной функцией — первое корректирующее устройство с передаточной функцией 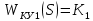 , ,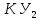 — второе корректирующее устройство с передаточной функцией — второе корректирующее устройство с передаточной функцией 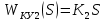 . .Заданы передаточные функции типовых звеньев и их параметры: 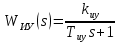 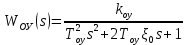 Где 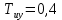 ; ;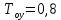 ; ;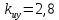 ; ;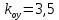 ; ;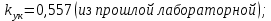 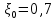 . .Требуется: С помощью метода D-разбиения в плоскости двух заданных параметров системы построить кривые D-разбиения, в том числе особые и концевые прямые, определить области, претендующие на устойчивость, и выбрать области устойчивости. Параметры для 4-ого варианта: 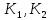 — неизвестные, — неизвестные, 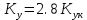 . .Ход работы Запишем передаточные функции всех элементов структурной схемы: 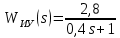 ; ;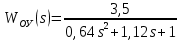 ; ;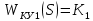 ; ;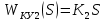 ; ;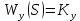 ; ; Рисунок 1 — Структурная схема системы для варианта 4 Преобразуя данную схему и подставляя передаточные функции, получим передаточную функцию замкнутой системы: 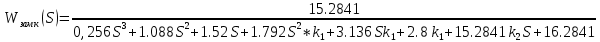 Запишем характеристический многочлен полученной передаточной функции: 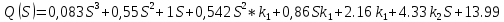 Неизвестными параметрами являются параметры: 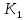 , , 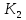 . .Для определения области параметров, претендующих на области устойчивости, воспользуемся методом D-разбиения. Для этого в характеристическом многочлене сделаем замену: 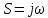 и приравняем действительную и мнимую части к нулю. и приравняем действительную и мнимую части к нулю.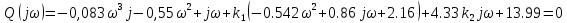 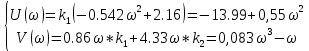 Решаем полученную систему относительно переменных 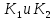 методом Крамера. методом Крамера.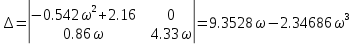 ; ;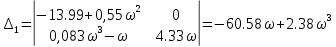 ; ;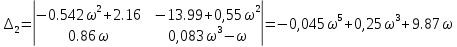 . .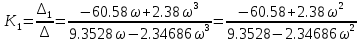 ; ;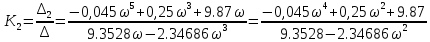 . .Далее проверим систему на наличие особых концевых линий. Приравняем определить 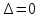 : :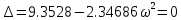 ; ;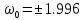 . .Система имеет особую линию при 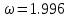 , однако эту линию можно не учитывать, так как , однако эту линию можно не учитывать, так как 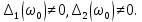 Приравняем коэффициент 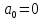 ; ;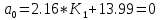 ; ;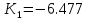 — уравнение концевой прямой. — уравнение концевой прямой.Для проверки области на устойчивость выберем набор значений параметров 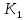 и и 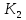 из областей-претендентов и при помощи критерия Гурвица проверим системы на устойчивость. из областей-претендентов и при помощи критерия Гурвица проверим системы на устойчивость.Выберем 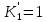 , , 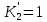 и подставим в характеристический многочлен: и подставим в характеристический многочлен: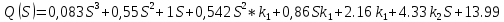 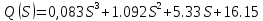 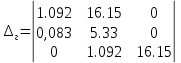 Для того, чтобы система была устойчивой, достаточно, чтобы выполнялось условие 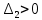 . .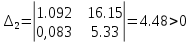 Делаем вывод, что выделенная область является областью устойчивости. Далее построим график переходного процесса при выбранный значения параметров 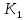 и и 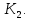 Передаточная функция системы имеет вид: 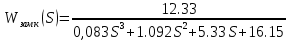 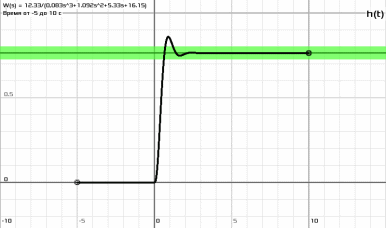 Рисунок 2 — График переходного процесса  Рисунок 3 — Полюса Выберем 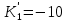 , , 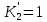 и подставим в характеристический многочлен: и подставим в характеристический многочлен: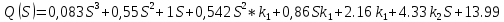 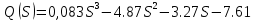  Рисунок 3 — Годограф амплитудно-фазовой характеристики Годограф Михайлова не начинается на вещественной положительной полуоси и не обходит последовательно 3 квадранта против часовой стрелки. Следовательно, линейная часть неустойчива. 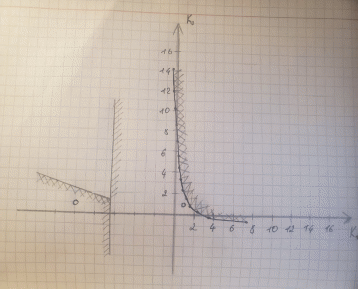 Вывод В данной лабораторной работе методом D-разбиения исследовались области устойчивости системы в плоскости двух параметров. Суть метода заключается в разбиении плоскости двух параметров на такие области, которые отличаются друг от друга количеством корней с отрицательной действительной частью, получаемыми набором параметров из каждой области. Для проверки области на устойчивость были выбраны пары значений параметров: 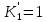 , , 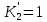 ; ; 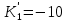 , , 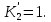 Выбранные значения подставлялись в характеристический многочлен, который далее исследовался на устойчивость при помощи критерия Гурвица. Выбранные значения подставлялись в характеристический многочлен, который далее исследовался на устойчивость при помощи критерия Гурвица.В результате получили то, что области оказались устойчивы, то есть любой набор параметров, взятый из данных областей, будет приводить систему к устойчивому состоянию. |
