Исследование одномерного плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах
 Скачать 69.66 Kb. Скачать 69.66 Kb.
|
|
Лабораторная работы №1. Исследование одномерного плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах 6.1 Краткая теория вопроса В данной лабораторной работе изучаются особенности фильтрации в слоисто-неоднородном круговом пласте, состоящем из двух пропластков с различной проницаемостью (Рис. 6.1, а) и зонально-неоднородном круговом пласте, состоящем из двух зон с различной проницаемостью (рис 6.1, б). 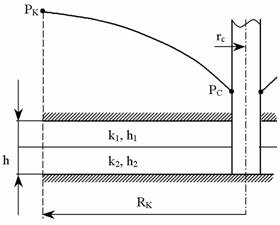 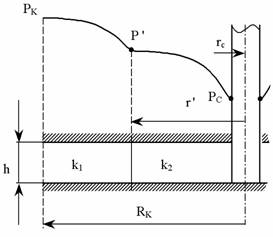 Рисунок 6.1, а Рисунок 6.1, б Рисунок 6.1 – Плоскорадиальный поток в слоисто-неоднородном (а) и зонально-неоднородном (б) пласте. Рассмотрим особенности фильтрации в слоисто- и зонально-неоднородных круговых пластах. а) случай слоисто-неоднородного пласта 1. При стационарной одномерной плоскорадиальной фильтрации несжимаемой жидкости по закону Дарси в слоисто-неоднородном пласте, состоящем из 2-х пропластков с различной проницаемостью К1 и К2 (рис. 6.1, а), распределение давления в каждом из пропластков носит логарифмический характер и определяется выражением 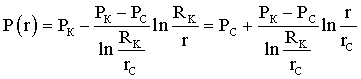 (6.1) (6.1)где Р(r) – установившееся давление на расстоянии r от скважины, Па; r – текущий радиус, м; Pк – установившееся пластовое давление на контуре питания Rк, Па; Rк – радиус контура питания пласта, м; Pс – установившееся давление в скважине, Па; rс – радиус скважины, м. 2. Градиенты давления в каждом пропластке одинаковы и определяются следующим выражением 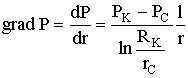 (6.2) (6.2)3. Скорости фильтрации по пропласткам: 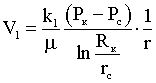 (6.3) (6.3) 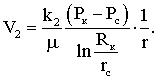 (6.4) (6.4)где μ - динамическая вязкость, Па·с. При равенстве градиентов давления в каждом пропластке из уравнений (6.3) – (6.4) следует справедливость следующего соотношения 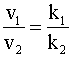 (6.5) (6.5)т.е. для слоисто-неоднородного кругового пласта скорости фильтрации по пропласткам прямо пропорциональны проницаемостям. Т.о. жидкость будет двигаться с опережением по более высокопроницаемому пропластку. Необходимо принимать меры по выравниванию фронтов движения жидкостей в пропластках с различной проницаемостью. 4. Выразим дебит скважины Q для случая слоисто-неоднородного пласта через kср: 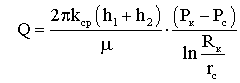 (6.6) (6.6)Но можно выразить и через сумму: 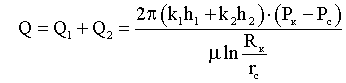 (6.7) (6.7)Приравнивая правые части уравнений, получим: 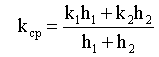 (6.8) (6.8)Или в общем виде 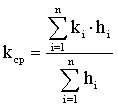 (6.9) (6.9)где n – количество пропластков; hi – толщина i-го пропластка с проницаемостью ki; б) случай зонально-неоднородного пласта В практике разработки нефтяных и газовых месторождений значительный интерес представляет задача о притоке жидкости к скважине при наличии вокруг забоя скважины кольцевой зоны с проницаемостью, отличной от проницаемости остальной части пласта, т.е. пласт состоит из двух зон различной проницаемости. Такая задача возникает в следующих случаях: при торпедировании или кислотной обработке призабойной зоны, установке гравийного фильтра, глинизации или парафинизации призабойной зоны, выносе мелких фракций породы из этой зоны и т.д. Очень важной при этом бывает необходимость установления влияния различия проницаемостей кольцевой призабойной зоны и остальной части пласта на продуктивность скважины При стационарной одномерной плоскорадиальной фильтрации несжимаемой жидкости по закону Дарси в зонально-неоднородном пласте, состоящем из 2-х зон с различной проницаемостью k1 и k2 (Рис. 6.1, б), распределение давления в каждой зоне подчиняется логарифмическому закону, но характер распространения пъезометрической линии зависит от давления Р' на границе этих зон: 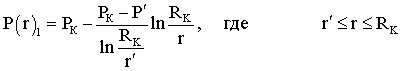 (6.10) (6.10)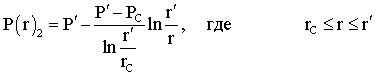 (6.11) (6.11)где Р(r)1 и Р(r)2 – установившееся давление на расстоянии r от скважины в первой и второй зонах соответственно, Па; r – текущий радиус, м; r' –радиус границы между первой и второй зоной, м; Р' – давление на границе этих зон, Па; Rк – радиус контура питания пласта, м; Pк – установившееся пластовое давление на контуре питания Rк, Па; rс – радиус скважины, м; Pс – установившееся давление в скважине, Па. 2.Распределение градиентов давления в каждой зоне подчиняется гиперболическому закону, но характер их распространения также зависит от давления Р' на границе этих зон: 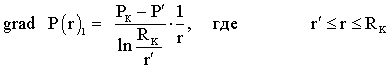 (6.12) (6.12)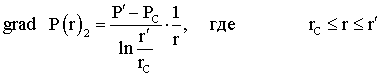 (6.13) (6.13)где grad P(r)1 и grad P(r)2 – градиенты давления в первой и второй зоне соответственно, Па/м. 3. Скорости фильтрации по зонам прямо пропорциональны градиентам давления в зонах: 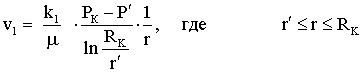 (6.14) (6.14)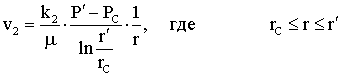 (6.15) (6.15)4. Дебит потока в силу установившегося движения несжимаемой жидкости будет постоянен через любую цилиндрическую поверхность, соосную скважине: 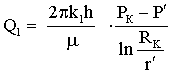 (6.16) (6.16)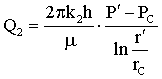 (6.17) (6.17)При наличии в пласте двух кольцевых зон (n=2) с различной проницаемостью давление P' на границе этих зон можно найти из равенства скоростей фильтрации на этой границе: 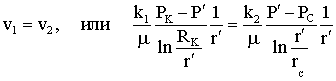 (6.18) (6.18)Откуда 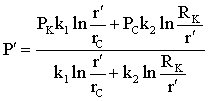 (6.19) (6.19)Подставив найденное значение давления P' на границе зон в уравнения (6.10) - (6.11), находим 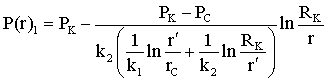 (6.20) (6.20)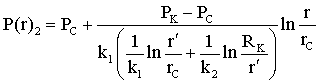 (6.21) (6.21)Аналогичным образом могут быть определены остальные характеристики рассматриваемого фильтрационного потока (градиенты давления, скорости фильтрации, объемные расходы жидкости по зонам). Дебит скважины в таком двухзональном пласте определится: 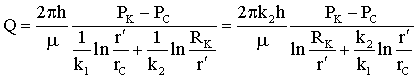 (6.22) (6.22)Среднее значение проницаемости зонально-неоднородного пласта можно определить из равенства дебитов аналогичных потоков в неоднородном и однородном пластах: 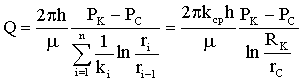 (6.23) (6.23)Откуда 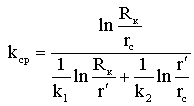 (6.24) (6.24)или в общем случае 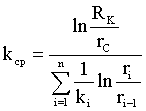 (6.25) (6.25)6.2 Цель и задачи лабораторной работы Целью лабораторной работы является исследование плоскорадиального установившегося фильтрационного потока несжимаемой жидкости в неоднородных пластах. Задачи лабораторной работы: 1) изучение влияния изменения проницаемости на распределение давления в слоисто- и зонально-неоднородных круговых пластах при установившейся фильтрации в них несжимаемой жидкости; 2) изучение характера изменения градиента давления и скорости фильтрации по радиусу слоисто- и зонально-неоднородных круговых пластов при установившейся фильтрации в них несжимаемой жидкости; 3) определение средней проницаемости слоисто- и зонально-неоднородных круговых пластов 6.3 Порядок выполнения работы Выполнение лабораторной работы осуществляется в соответствии с индивидуальным вариантом задания, устанавливаемым преподавателем. Варианты заданий приведены в таблице 5.1. 1. При изучении характеристик рассматриваемых (слоисто- и зонально-неоднородного) фильтрационных потоков несжимаемой жидкости получить формулы и изобразить графически распределения давления, градиента давления и скорости фильтрации в зависимости от текущего радиуса r (в соответствии с формулами (6.1) - (6.4)) и (6.10) - (6.15)). Значения текущего радиуса r выбрать следующие 10, 25, 50, 75, 100 м и далее через 200 метров. 2. Для слоисто-неоднородного кругового пласта убедиться в правильности соотношения (6.5). Определить объемные расходы по пропласткам и по всему пласту в целом (6.7). Выразить объемные расходы в м3/с и м3/сут. Определить средний коэффициент проницаемости для слоисто-неоднородного пласта (6.8). 4. Для зонально-неоднородного кругового пласта определить давление на границе зон Р´ (6.19), объемные расходы по зонам (6.16)-(6.17) и по всему пласту в целом (6.23). Выразить объемные расходы в м3/с и м3/сут. Определить средний коэффициент проницаемости для зонально-неоднородного пласта (6.24). 5. Провести анализ и оценку полученных результатов, сделать необходимые пояснения и выводы. В выводах сформулировать полученные результаты с акцентом на выполнение задач лабораторной работы. Перечень вопросов к самоподготовке 1. Дайте характеристику различных типов неоднородности пластов. 2. Каковы особенности фильтрации жидкости в неоднородных пластах? 3. Напишите основные формулы распределения давления, средней проницаемости и соотношения градиентов давления в зонах для неоднородных по проницаемости пластов. 4. Перечислите основные задачи лабораторной работы. 5. Каково практическое значение изучения фильтрации в неоднородных пластах? Исходные данные для расчетов
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
