Теория по математической статистике. Математическая статистика. Теория
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
Математическая статистика. Теория. Дайте определение случайной величины, которая имеет гамма-распределение 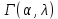 и выведите основные свойства гамма-распределения. Запишите формулы для математического ожидания и дисперсии гамма-распределения. и выведите основные свойства гамма-распределения. Запишите формулы для математического ожидания и дисперсии гамма-распределения.Определение: Случайная величина 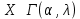 (имеет гамма-распределение), если плотность распределения (имеет гамма-распределение), если плотность распределения 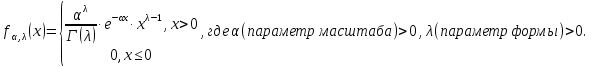 Основные свойства гамма-распределения: В частности, если 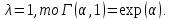 Гамма-распределение бесконечно делимо (на лекциях этого не было, взято из интернета). Если 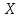 и и 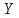 – независимые случайные величины, – независимые случайные величины, 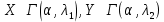 , то , то 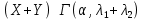 . .Если 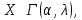 а а 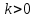 – произвольная константа, то – произвольная константа, то 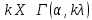 (это тоже). (это тоже).Пусть 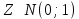 и пусть и пусть 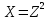 . Тогда . Тогда 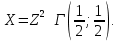 Математическое ожидание и дисперсия: Если 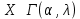 , то , то 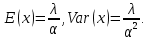 Дайте определение случайной величины, которая имеет 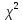 -распределение с -распределение с 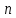 степенями свободы. Запишите плотность степенями свободы. Запишите плотность 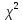 -распределения. Выведите формулы для математического ожидания и дисперсии -распределения. Выведите формулы для математического ожидания и дисперсии 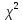 -распределения с -распределения с 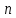 степенями свободы. степенями свободы.Определение: Пусть 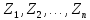 – независимые одинаково распределенные случайные величины, – независимые одинаково распределенные случайные величины, 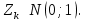 Обозначим Обозначим 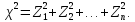 Распределение случайной величины 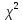 называется распределением хи-квадрат с называется распределением хи-квадрат с 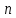 степенями свободы. степенями свободы.Обозначение: 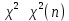 . .Плотность: Пусть 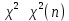 , тогда плотность распределения имеет следующий вид: , тогда плотность распределения имеет следующий вид: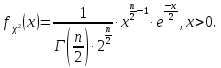 Математическое ожидание и дисперсия: Если 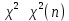 , то , то 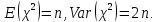 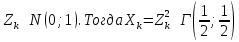 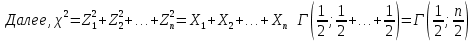 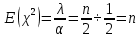 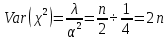 Дайте определение случайной величины, которая имеет распределение Стьюдента с 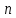 степенями свободы. Как связаны распределение Коши и распределение Стьюдента? Запишите плотность распределения Стьюдента с 4 степенями свободы. степенями свободы. Как связаны распределение Коши и распределение Стьюдента? Запишите плотность распределения Стьюдента с 4 степенями свободы.Определение: Распределение случайной величины 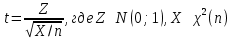 , называется распределением Стьюдента с , называется распределением Стьюдента с 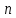 степенями свободы. степенями свободы.Обозначение: 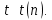 Плотность 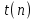 задается формулой: задается формулой: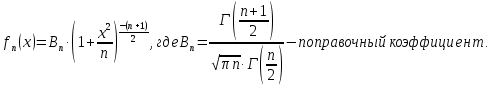 Связь распределения Коши и распределения Стьюдента: Стандартное распределение Коши является частным случаем распределения Стьюдента: 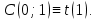 Плотность распределения с 4 степенями свободы: 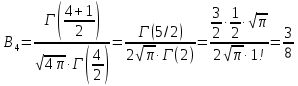 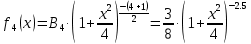 Дайте определение случайной величины, которая имеет распределение Фишера 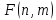 с с 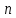 и и 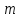 степенями свободы. Запишите плотность распределения Фишера степенями свободы. Запишите плотность распределения Фишера 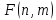 с с 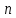 и и 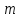 степенями свободы. Какой закон распределения имеет случайная величина степенями свободы. Какой закон распределения имеет случайная величина 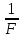 , если случайная величина , если случайная величина 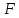 имеет распределение Фишера имеет распределение Фишера 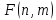 с с 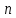 и и 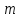 степенями свободы? Ответ необходимо обосновать. степенями свободы? Ответ необходимо обосновать.Определение: Пусть 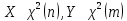 – независимые случайные величины. Распределение случайной величины – независимые случайные величины. Распределение случайной величины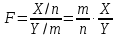 называется распределением Фишера с 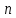 и и 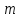 степенями свободы. степенями свободы.Обозначение: 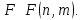 Плотность: Пусть 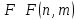 , тогда плотность определяется формулой: , тогда плотность определяется формулой: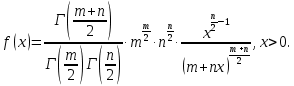 Распределение 1/F: Пусть 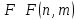 , тогда , тогда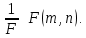 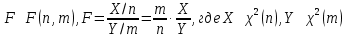 – независимые случайные величины. – независимые случайные величины.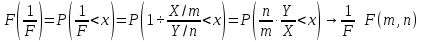 Дайте определения процентной точки и квантили. Укажите связь между процентными точками и квантилями. Сформулируйте основные свойства процентных точек. Выведите формулу для нахождения процентной точки стандартного нормального закона распределения через функцию Лапласа 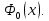 Определение: 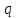 -квантилем (или квантилем уровня/порядка -квантилем (или квантилем уровня/порядка 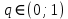 или левосторонней критической границей) называется решение уравнения или левосторонней критической границей) называется решение уравнения 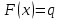 , где , где 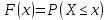 – функция распределения. – функция распределения.Квантиль уровня 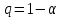 называется называется 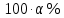 процентной точкой и обозначается процентной точкой и обозначается 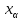 (или называется правосторонней критической границей или верхней процентной точкой). (или называется правосторонней критической границей или верхней процентной точкой). 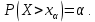 Связь между квантилем и процентной точкой: 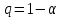 Свойства процентных точек: 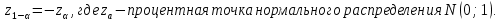 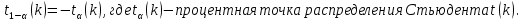 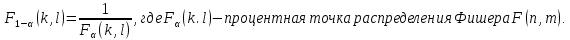 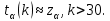 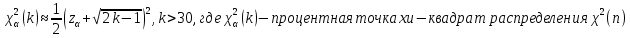 . .Формула нахождения процентной точки стандартного нормального закона через функцию Лапласа: 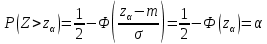 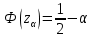 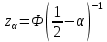 Сформулируйте определение случайной выборки из конечной генеральной совокупности. Какие виды выборок вам известны? Перечислите (с указанием формул) основные характеристики выборочной и генеральной совокупностей. Случайной выборкой из конечной генеральной совокупности называют результат множества наблюдений 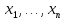 , где n – объем выборки, отобранной случайным образом из генеральной совокупности. , где n – объем выборки, отобранной случайным образом из генеральной совокупности.По методу отбора различают повторную и бесповторную выборки. Повторной выборкой называется совокупность, образованная по следующей схеме: сначала из генеральной совокупности случайным равновероятным образом извлекается один элемент; затем этот элемент возвращается в генеральную совокупность и все повторяется, пока не будет отобрано необходимое число элементов. Бесповторной выборкой называется совокупность, образованная по аналогичной схеме, но с одним отличием – отобранные элементы в генеральную совокупность не возвращаются.
Здесь ‘x=Х – случайная величина. Сформулируйте определение случайной выборки из распределения. Как в этом случае определяются: выборочное среднее, начальные и центральные моменты выборки, функция распределения выборки? Что в данном контексте означает генеральное среднее? Случайной выборкой объёма n из распределения ℒ назыв. набор Х1,…,Хn – n случ. вел. с одним и тем же законом распределения ℒ. Выборочное (эмпирическое) среднее 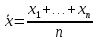 начальный момент 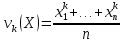 центральный момент 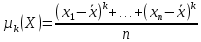 функция распределения 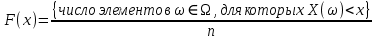 Генеральное среднее ‒ среднее арифметическое значений признака генеральной совокупности 1. Если значения признака различны, то 2. Если значения признака имеют частоты Запишите формулы для математического ожидания и дисперсии выборочной доли в случае повторной (бесповторной) выборки. Поясните все используемые обозначения. Отношение 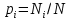 (соответственно (соответственно 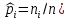 называется генеральной (соответственно выборочной) долей значения xi признака X. Где называется генеральной (соответственно выборочной) долей значения xi признака X. Где 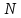 и и 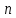 объем генеральной и выборочной совокупности соответственно. объем генеральной и выборочной совокупности соответственно.Пусть p – генеральная, а 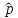 – выборочная доля какого-либо значения x1 признака X, q=1-p. Тогда: – выборочная доля какого-либо значения x1 признака X, q=1-p. Тогда:в случае повторной или бесповторной выборки 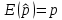 в случае повторной выборки 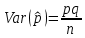 в случае бесповторной выборки 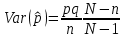 Сформулируйте определение выборочной функции распределения и докажите ее сходимость по вероятности к теоретической функции распределения. Выведите формулы для математического ожидания и дисперсии выборочной функции распределения. См определение в док-ве. Эмпирическая ф.р. = выборочная ф.р.  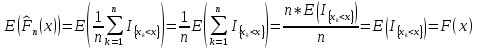 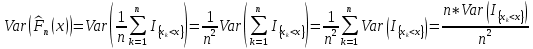 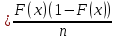 Дайте определение k-ой порядковой статистики. Выведение формулы для функций распределений экстремальных статистик. Пусть {\displaystyle X_{1},\ldots ,X_{n}} 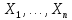 - конечная выборка из некоторого распределения{\displaystyle \mathbb {P} ^{X}}, определённая на некотором вероятностном пространстве (ꭥ, Ƒ, · ){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}. Пусть - конечная выборка из некоторого распределения{\displaystyle \mathbb {P} ^{X}}, определённая на некотором вероятностном пространстве (ꭥ, Ƒ, · ){\displaystyle (\Omega ,{\mathcal {F}},\mathbb {P} )}. Пусть 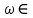 {\displaystyle \omega \in \Omega } ꭥ и {\displaystyle \omega \in \Omega } ꭥ и 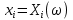 {\displaystyle x_{i}=X_{i}(\omega ),\;i=1,\ldots ,n}. Перенумеруем последовательность {\displaystyle \{x_{i}\}_{i=1}^{n}} {\displaystyle x_{i}=X_{i}(\omega ),\;i=1,\ldots ,n}. Перенумеруем последовательность {\displaystyle \{x_{i}\}_{i=1}^{n}}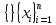 в порядке неубывания, так что в порядке неубывания, так что 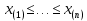 . .Эта последовательность называется вариационным рядом. Вариационный ряд и его члены являются порядковыми статистиками. Случайная величина 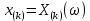 {\displaystyle X_{(k)}(\omega )=x_{(k)}}называется {\displaystyle k}k-ой порядковой статистикой исходной выборки. {\displaystyle X_{(k)}(\omega )=x_{(k)}}называется {\displaystyle k}k-ой порядковой статистикой исходной выборки.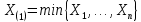 и и 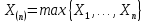 – экстремальные статистики. – экстремальные статистики.Ф-ия распред. 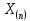 : :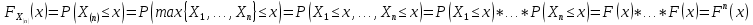 Ф-ия распред. 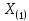 : :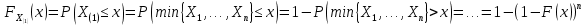 |
