Теория по математической статистике. Математическая статистика. Теория
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
|
Что такое точечная статистическая оценка? Какие оценки называются несмещенными, состоятельными? Приведите пример оценки с минимальной дисперсией. Пусть 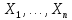 - выборка из - выборка из 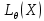 . Статистика . Статистика 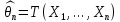 (вычисляемая по выборочным данным), предназначенная для приближенного вычисления параметра (вычисляемая по выборочным данным), предназначенная для приближенного вычисления параметра 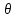 называется точечной статистической оценкой параметра называется точечной статистической оценкой параметра 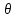 . .Статистическая оценка 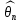 параметра параметра 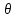 называется несмещенной в среднем (несмещенной), если называется несмещенной в среднем (несмещенной), если 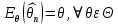 . .Статистическая оценка 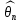 параметра параметра 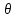 называется состоятельной, если называется состоятельной, если 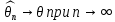 , т. е. , т. е. 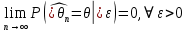 Пример: относительная частота 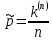 успехов в серии из n испытаний по схеме Бернулли – эффективная оценка вероятности успеха р. успехов в серии из n испытаний по схеме Бернулли – эффективная оценка вероятности успеха р.Сформулируйте и докажите достаточное условие состоятельности оценки. Если 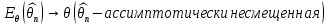 и и 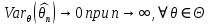 , то , то 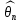 - состоятельная оценка. г - состоятельная оценка. гДоказательство: 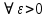 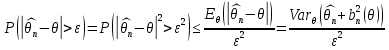 , , 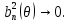 Таким образом, правую часть можно сделать сколь угодно маленькой, т. е. 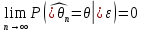 , т. е. , т. е. 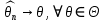 . .Сформулируйте определение среднеквадратичной ошибки оценки. Какая оценка называется оптимальной? В чем заключается среднеквадратический подход к сравнению оценок? Определим среднеквадратичную ошибку оценки 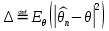 Пусть 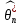 и и 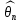 -две несмещенные оценки. Если -две несмещенные оценки. Если 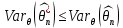 , , 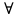 несмещенной оценки несмещенной оценки 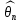 , то , то 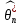 называется несмещенной оценкой с равномерно минимальной дисперсией (НОРМД) или оптимальной оценкой. называется несмещенной оценкой с равномерно минимальной дисперсией (НОРМД) или оптимальной оценкой.Оценка 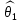 лучше лучше 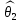 , в смысле среднеквадратической ошибки, если , в смысле среднеквадратической ошибки, если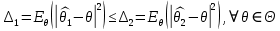 Сформулируйте критерий оптимальности оценки, основанной на неравенстве Рао–Крамера. Оценка 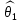 называется эффективной по Рао-Крамера, если называется эффективной по Рао-Крамера, если  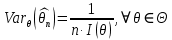 Эффективная оценка (если она существует) является оптимальной. Дайте определение информации по Фишеру и сформулируйте информационное неравенство Рао–Крамера. Опр: Информация по Фишеру для одного наблюдения X называется 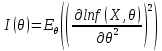 , , 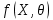 - плотность распределения - плотность распределения 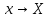 Теорема(Информационное неравенство Рао-Крамера): Пусть 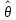 -несмещенная оценка в параметрической регулярной (для которой выполнены условия регулярности) модели -несмещенная оценка в параметрической регулярной (для которой выполнены условия регулярности) модели 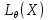 . Тогда справедливо неравенство: . Тогда справедливо неравенство: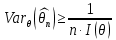 Сформулируйте определение эффективной оценки по Рао–Крамеру. Найдите эффективную оценку параметра 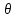 для распределения Бернулли для распределения Бернулли 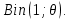  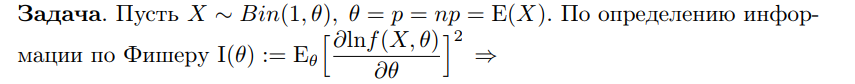 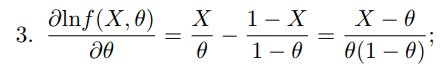 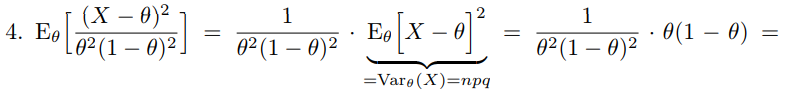 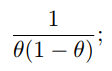  Докажите несмещенность, состоятельность и эффективность (в классе всех линейных несмещенных оценок) выборочного среднего 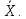 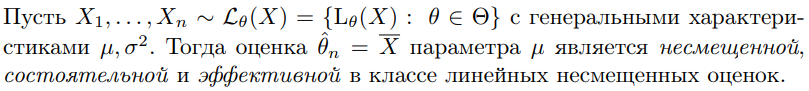 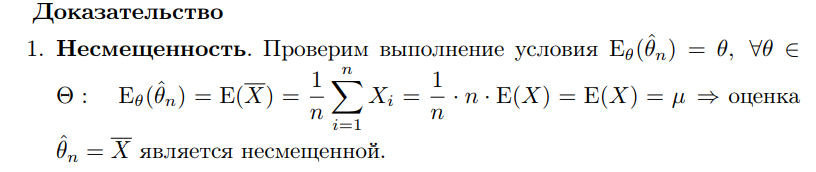   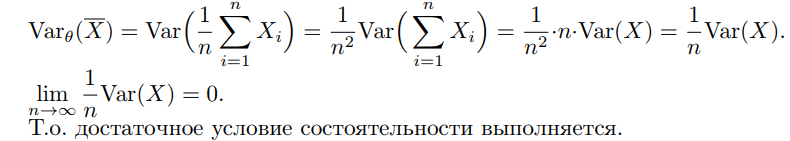  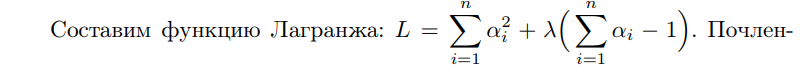  Сформулируйте определение эффективной оценки по Рао–Крамеру. Для распределения Пуассона 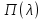 предлагается оценка параметра предлагается оценка параметра 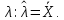 Покажите, что эта оценка является эффективной по Рао–Крамеру. Покажите, что эта оценка является эффективной по Рао–Крамеру. 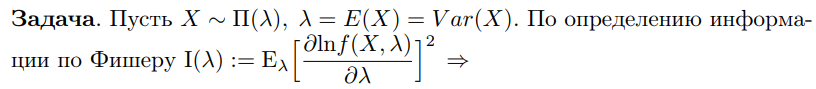  Сформулируйте информационное неравенство Рао–Крамера. Исследуйте на эффективность оценку 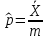 для биномиального распределения для биномиального распределения 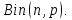    Дайте определение информации по Фишеру. Вычислите информацию Фишера для нормального закона распределения 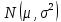 (дисперсия (дисперсия 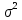 известна) и проверьте, что выборочное среднее известна) и проверьте, что выборочное среднее 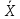 является эффективной оценкой параметра является эффективной оценкой параметра 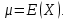 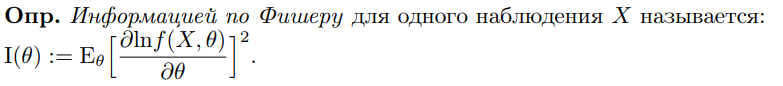 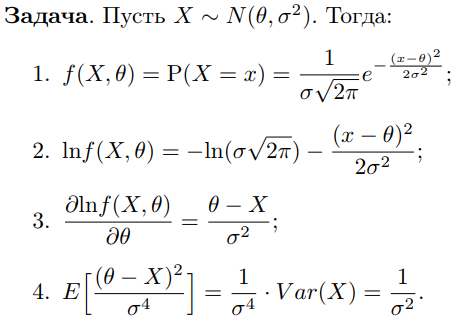  Сформулируйте информационное неравенство Рао–Крамера. Пусть 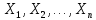 – выборка объема – выборка объема 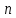 из показательного закона распределения с параметром из показательного закона распределения с параметром 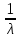 , где , где 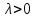 . Проверьте, используя неравенство Рао–Крамера, является ли оценка . Проверьте, используя неравенство Рао–Крамера, является ли оценка 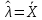 параметра параметра 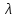 эффективной? эффективной?Пусть 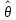 -несмещенная оценка в параметрической регулярной модели -несмещенная оценка в параметрической регулярной модели 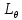 (X), тогда справедливо неравенство: (X), тогда справедливо неравенство: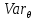 ( (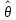 n) ≥ n) ≥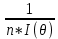 Найдем информацию по Фишеру относительно параметра λ: I(λ)= 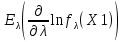 2 2 Плотность данного показательного распределения имеет вид: 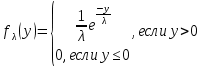 Тогда, 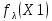 = =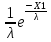 , ln , ln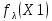 = - lnλ- = - lnλ-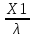 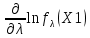 = - = -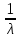 + +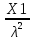 = = 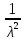 (X1- (X1-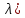 , ,I(λ)= 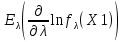 2 = 2 = 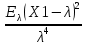 = = 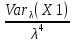 = = 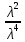 = = 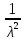 Теперь найдем дисперсию оценки   = =  = = Подставив дисперсию и информацию по Фишеру в неравенство Рао-Крамера, получаем равенство, следовательно, оценка 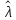 = =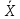 является эффективной. является эффективной.Дайте определение информации по Фишеру 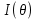 для одного наблюдения для одного наблюдения 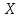 и докажите формулу и докажите формулу 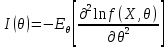 . .Информацией по Фишеру для одного наблюдения Х называется I(θ)= 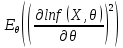 . .Доказательство равенства: 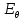 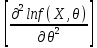 = =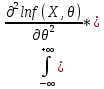 f dx= f dx=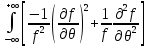 f dx = - f dx = -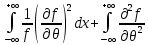 dx = -I (Так как первый интеграл равен I, а второй – 0). dx = -I (Так как первый интеграл равен I, а второй – 0).Как производится оценка параметров абсолютно непрерывного распределения методом максимального правдоподобия? Какой вероятностный смысл в этом случае имеет функция правдоподобия? Приведите пример функции правдоподобия для параметра непрерывного распределения. Пусть генеральная совокупность определяется случайной величиной ξ с функцией распределения F(x, θ) и задана выборка (X1, . . . , Xn). Суть метода состоит в нахождении такого значения 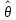 неизвестного параметра θ, при котором вероятность реализации (x1, . . . , xn) вектора (X1, . . . , Xn) была бы максимальна. неизвестного параметра θ, при котором вероятность реализации (x1, . . . , xn) вектора (X1, . . . , Xn) была бы максимальна. Пусть ξ – непрерывная случайная величина с плотностью f(x, θ), где θ – неизвестный параметр. Тогда f(x1, . . . , xn, θ) = f(x1, θ) · . . . · f(xn, θ) – плотность распределения вектора (X1, . . . , Xn). Для непрерывной случайной величины функция L(x1, . . . , xn, θ) = f(x1, θ) · . . . · f(xn, θ), (68) рассматриваемая при фиксированных (x1, . . . , xn) как функция параметра θ, называется функцией правдоподобия. Пример Пусть Х1,…,Хn— выборка объема n из равномерного распределения U([θ;θ+5]), где  Выпишем плотность распределения и функцию правдоподобия. Плотность: f(x,θ)=  Тогда функция правдоподобия:   Как производится оценка параметров распределения методом моментов? Найдите методом моментов оценку параметра 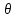 равномерного распределения равномерного распределения 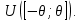 Рассмотрим случайную величину ξ с плотностью f(x, θ) и выборку объема n (x1, . . . , xn). У случайной величины ξ существуют моменты ν1, . . . , νn, которые являются функциями от θ. Выборочные моменты νk вычисляют по формуле νk = 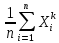 = =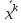 Приравнивая выборочные и теоретические моменты, получаем уравнения относительно параметра θ. Пусть уравнения однозначно и непрерывно разрешимы относительно θ. Решая эти уравнения, получаем оценку 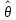 параметра θ. Эта оценка называется оценкой метода моментов и обозначается о.м.м. параметра θ. Эта оценка называется оценкой метода моментов и обозначается о.м.м.ν1= 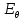 (X)= (X)= 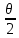 ; ; 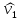 = =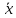 ν1(θ)= 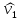 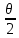 = = 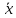 => => 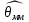 = 2 = 2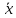 k=2, 3, … νk(θ) = 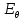 (Xk) = (Xk) = 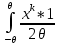 dx = dx = 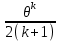 - - 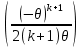 = = 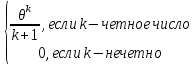 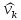 = νk(θ) <=> = νk(θ) <=> 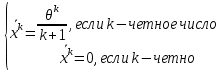 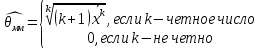 |
