Теория по математической статистике. Математическая статистика. Теория
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
Y = (Пояснив используемые символы, запишите симметричный по вероятности 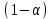 - доверительный интервал для дисперсии при неизвестном математическом ожидании. Предполагается ли в этом случае нормальность генерального распределения? - доверительный интервал для дисперсии при неизвестном математическом ожидании. Предполагается ли в этом случае нормальность генерального распределения?Интервал 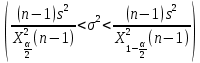 является (1-α) – доверительным для является (1-α) – доверительным для 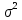 в нормальной модели N(m, в нормальной модели N(m, 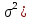 , когда параметр m=E(x) неизвестен. , когда параметр m=E(x) неизвестен.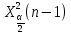 – критическая точка хи-квадрат распределения с уровнем значимости – критическая точка хи-квадрат распределения с уровнем значимости 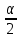 с (n-1) степенями свободы с (n-1) степенями свободы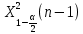 - критическая точка хи-квадрат распределения с уровнем значимости - критическая точка хи-квадрат распределения с уровнем значимости 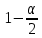 с (n-1) степенями свободы с (n-1) степенями свободыS2 – исправленная выборочная дисперсия, которая считается по формуле s2= 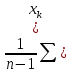 - -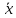 )2. )2.Как связаны эффективная оценка по Рао–Крамеру (если она существует) и оценка максимального правдоподобия? Ответ необходимо обосновать. Пусть 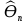 - несмещенная оценка параметра - несмещенная оценка параметра 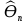 в параметрической модели в параметрической модели 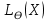 , для которой выполнены условия регулярности, тогда справедливо: , для которой выполнены условия регулярности, тогда справедливо: 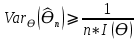 . Для эффективной оценки . Для эффективной оценки 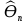 неравенство становится равенством. неравенство становится равенством.Если существует эффективная оценка 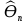 в смысле Рао-Крамера, то в смысле Рао-Крамера, то 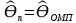 . .Док-во: В этом случае имеет место уравнение факторизации 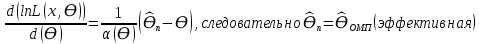 . .Сформулируйте определение доверительной оценки параметра с коэффициентом доверия 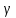 . .Пусть 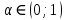 . Будем говорить, что две статистики определяют границы доверительного интервала . Будем говорить, что две статистики определяют границы доверительного интервала 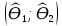 с коэффициентом доверия с коэффициентом доверия 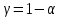 , если , если 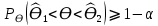 . .Приведите формулы (с выводом) доверительного интервала для нормальной модели 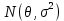 , когда параметр масштаба , когда параметр масштаба 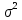 известен, а параметр сдвига известен, а параметр сдвига 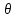 не известен. не известен.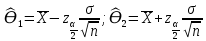 Вывод формулы. 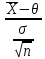 - стандартаная нормальная случайная величина. - стандартаная нормальная случайная величина.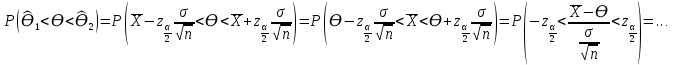 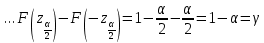 Приведите формулы (свыводом) доверительного интервала параметра сдвига 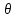 для нормальной модели для нормальной модели 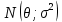 , когда параметр масштаба , когда параметр масштаба 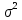 неизвестен. неизвестен.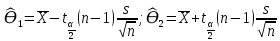 Вывод формулы. 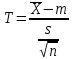 - случайная величина; - случайная величина; 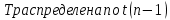 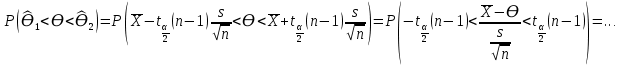 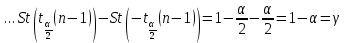 Дайте определение асимптотически доверительного интервала и приведите формулы асимтотически доверительного интервала коэффициента корреляции 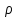 для двумерной нормальной модели. для двумерной нормальной модели.Ассимптотическим доверительным интервалом параметра 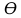 называется такой интервал называется такой интервал 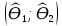 , который с коэффициентом , который с коэффициентом 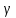 обладает свойством: обладает свойством: 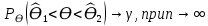 . . 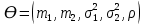 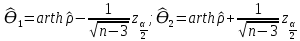 Какие выборки называются однородными? Сформулируйте критерий Пирсона по проверке с заданным уровнем значимости 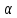 гипотезы об однородности нескольких выборок. гипотезы об однородности нескольких выборок.Гипотеза однородности или задача о двух выборках: Пусть X=(X1,...,Xn) выборка из распределения 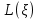 с некоторой неизвестной функцией распределения F1(x), а Y=(Y1,...,Ym) выборка из распределения с некоторой неизвестной функцией распределения F1(x), а Y=(Y1,...,Ym) выборка из распределения 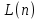 с неизвестной функцией распределения F2(x). Гипотезой однородности является утверждение H0: с неизвестной функцией распределения F2(x). Гипотезой однородности является утверждение H0: 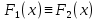 Критерий однородности Пирсона хи-квадрат. Применяется к дискретным данным, конечное число N>=2 различных значений. 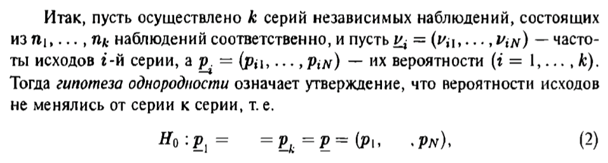  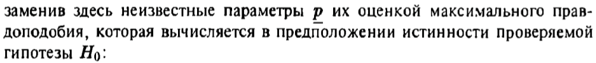  Какие выборки называются однородными? Сформулируйте критерий Колмогорова–Смирнова по проверке с заданным уровнем значимости 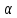 гипотезы об однородности двух выборок. гипотезы об однородности двух выборок.Гипотеза однородности или задача о двух выборках: Пусть X=(X1,...,Xn) выборка из распределения 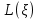 с некоторой неизвестной функцией распределения F1(x), а Y=(Y1,...,Ym) выборка из распределения с некоторой неизвестной функцией распределения F1(x), а Y=(Y1,...,Ym) выборка из распределения 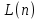 с неизвестной функцией распределения F2(x). Гипотезой однородности является утверждение H0: с неизвестной функцией распределения F2(x). Гипотезой однородности является утверждение H0: 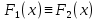 Критерий однородности Колмогорова–Смирнова. Тестовая статистика 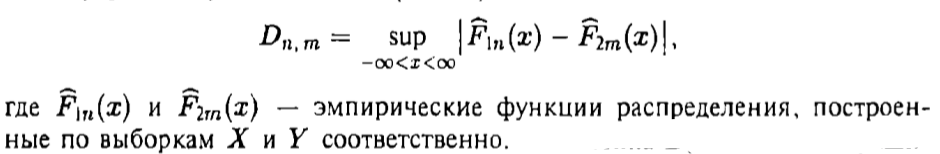 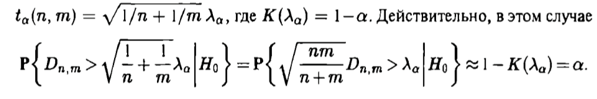  Определите P-значение статистического критерия. Каким образом находится P-значение, если известно распределение статистики критерия 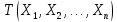 ? Рассмотрите случай критической области вида ? Рассмотрите случай критической области вида 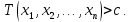 Пусть есть статистический критерий (X1,X2,...,Xn) с критической областью K и пусть имеется реализация 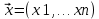 случайной выборки случайной выборки 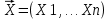 . P-значением критерия PV( . P-значением критерия PV(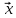 ) называется наименьшая величина уровня значимости при котором H0 отвергается PV( ) называется наименьшая величина уровня значимости при котором H0 отвергается PV(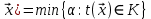 Предположи что PV( 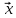 ) удалось получить из определения следует что 1) если ) удалось получить из определения следует что 1) если 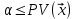 то гипотеза H0 принимается 2) иначе отвергается то гипотеза H0 принимается 2) иначе отвергаетсяПусть T(X1,X2,...,Xn)=T( 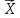 ) статистика критерия и случ. вел., t(x1,x2,...,xn)=t( ) статистика критерия и случ. вел., t(x1,x2,...,xn)=t(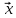 ) значение статистики критерия, тогда ) значение статистики критерия, тогдаЕсли k={ t(x1,x2,...,xn)>c2} то p1= 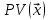 = =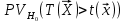 Если k={ t(x1,x2,...,xn) 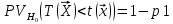 Если k={ t(x1,x2,...,xn)>c2 и t(x1,x2,...,xn) Сформулируйте общую схему проверки гипотезы о вероятностях событий, образующих полную группу, по критерию Пирсона без оценки неизвестных параметров. ПРОПИСАТЬ. Сформулируйте односторонний, с заданным уровнем значимости 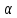 , критерий по проверке гипотезы о равенстве средних двух нормальных генеральных распределений с неизвестными равными дисперсиями. Укажите также двусторонний вариант данного критерия. , критерий по проверке гипотезы о равенстве средних двух нормальных генеральных распределений с неизвестными равными дисперсиями. Укажите также двусторонний вариант данного критерия.Пусть X |
 | K |
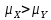 | 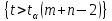 |
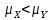 | 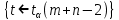 |
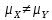 | 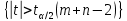 |
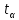 (m + n − 2) – верхняя процентная точка распределения Стьюдента с m + n − 2 степенями свободы, α – требуемый уровень значимости.
(m + n − 2) – верхняя процентная точка распределения Стьюдента с m + n − 2 степенями свободы, α – требуемый уровень значимости.Опишите общую схему проверки статистических гипотез. Определите понятия: критическая область, уровень значимости, мощность критерия. Какие гипотезы называются простыми(сложными)?
Пусть
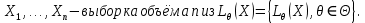 Статистической гипотезой называется любое утверждение о виде или о параметрах
Статистической гипотезой называется любое утверждение о виде или о параметрах 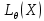 . Параметрическая гипотеза – простая, если она имеет вид θ=
. Параметрическая гипотеза – простая, если она имеет вид θ=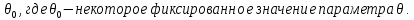 Если θ∈Θ, где Θ содержит по крайней мере 2 элемента, то гипотеза – сложная.
Если θ∈Θ, где Θ содержит по крайней мере 2 элемента, то гипотеза – сложная. Пусть K – некоторое подмножество
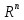 . Статистическим критерием с критической областью K⊂
. Статистическим критерием с критической областью K⊂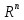 называется правило, в соответствии с которым
называется правило, в соответствии с которым 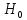 отвергается, если выборка (
отвергается, если выборка (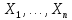 ) попадает в критическую область К, т.е.
) попадает в критическую область К, т.е. 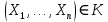 , и принимается, если
, и принимается, если 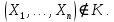
Ошибка I рода: отвергается
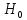 , когда, на самом деле, она верна.
, когда, на самом деле, она верна.Ошибка II рода: отвергается
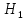 , когда, на самом деле, верна.
, когда, на самом деле, верна.Вероятность ошибки I рода называется уровнем значимости критерия α.
Вероятность ошибки II рода называется уровнем значимости критерия β.
Мощность критерия: W=1-β.
Приведите вероятностную интерпретацию ошибок первого и второго рода, а также мощности критерия в случае простых нулевой и альтернативной гипотез.
Вероятность ошибок I и II рода и мощность критерия находятся в соответствии с таблицей:
t:
 , c = const
, c = const| Критическая область для 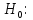 K={t > c} K={t > c} | Критическая область для 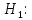 K={t < c} K={t < c} |
| α= 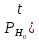 ( (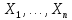 )>c) )>c) | α= 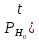 ( (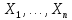 ) ) |
| β= 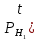 ( (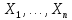 )≤c) )≤c) | β= 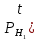 ( (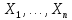 )≥c) )≥c) |
| W= 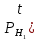 ( (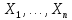 )>c) )>c) | W= 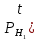 ( (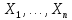 ) ) |

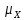 ,
, 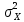 ), а
), а 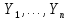 )– выборка из нормального распределения N(
)– выборка из нормального распределения N(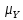 ,
, 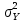 ). Выборки X и Y независимы. Генеральные дисперсии
). Выборки X и Y независимы. Генеральные дисперсии 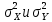 - неизвестны, но равны:
- неизвестны, но равны: 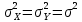 .
. 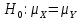
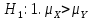 , 2.
, 2. 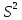 параметра
параметра 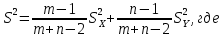
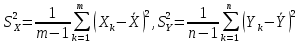
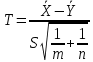
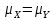 ), то случ. величина T∼t(m + n - 2) распределена по закону Стьюдента.
), то случ. величина T∼t(m + n - 2) распределена по закону Стьюдента.