Теория по математической статистике. Математическая статистика. Теория
 Скачать 1.99 Mb. Скачать 1.99 Mb.
|
Y = (Сформулируйте односторонний, с заданным уровнем значимости 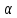 , критерий по проверке гипотезы о равенстве средних двух нормальных генеральных совокупностей с известными дисперсиями. Укажите также двусторонний вариант данного критерия. , критерий по проверке гипотезы о равенстве средних двух нормальных генеральных совокупностей с известными дисперсиями. Укажите также двусторонний вариант данного критерия.Пусть X | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
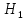 | K |
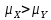 | 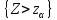 |
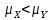 | 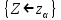 |
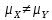 | 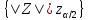 |
Где
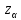 - процентная точка стандартного нормального распределения N(0;1), т.е.
- процентная точка стандартного нормального распределения N(0;1), т.е. 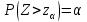 – уровень значимости.
– уровень значимости.Сформулируйте односторонний, с заданным уровнем значимости
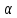 , критерий по проверке гипотезы о равенстве дисперсий двух нормальных генеральных распределений. Укажите также двусторонний вариант данного критерия.
, критерий по проверке гипотезы о равенстве дисперсий двух нормальных генеральных распределений. Укажите также двусторонний вариант данного критерия.Пусть имеются 2 независимые выборки из нормальных распределений:
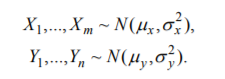
Далее считаем, что все четыре параметра
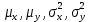 неизвестны. В качестве основной гипотезы примем
неизвестны. В качестве основной гипотезы примем 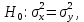 а в качестве альтернативной – одну из трех гипотез:
а в качестве альтернативной – одну из трех гипотез:1)
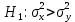
2)
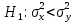
3)
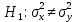
При построении критериев по проверке
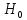 с заданным уровнем значимости применяется следующая теорема.
с заданным уровнем значимости применяется следующая теорема.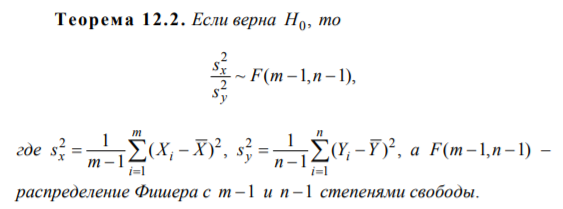

Сформулируйте лемму Неймана–Пирсона в случае проверки двух простых гипотез. Приведите пример построения наиболее мощного критерия.


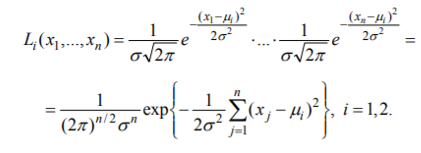



Сформулируйте критерий независимости хи-квадрат Пирсона. Приведите явный вид статистики критерия в случае 2x2-таблицы сопряженности.
Пусть есть 2 дискретные случайные величины X, Y. Требуется проверить, что X и Y независимы.
Пусть
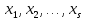 – возможные значения X
– возможные значения X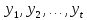 – возможные значения Y.
– возможные значения Y.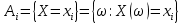
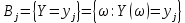 Множество значений случайной величины Z = (X, Y) распадается на N = s*t прямоугольников вида
Множество значений случайной величины Z = (X, Y) распадается на N = s*t прямоугольников вида 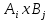 .
.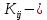 число наблюдений (пар) вида (
число наблюдений (пар) вида (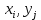 ).
). 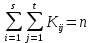 .
.Таблица сопряжённости:
| X | Y | Σ | ||||
| B1 | B2 | … | Bt | |||
| A1 | K11 | K12 | … | K1t | 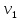 | |
| A2 | K21 | K22 | … | K2t | 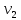 | |
| … | … | … | … | … | … | |
| As | Ks1 | Ks2 | … | Kst | 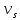 | |
| Σ | 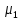 | 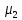 | … | 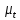 | | |
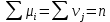 , где
, где 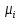 – сколько раз наблюдалось
– сколько раз наблюдалось 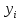 по всем рядам,
по всем рядам, 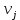 – сколько раз наблюдалось значение
– сколько раз наблюдалось значение 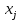 .
.Пусть
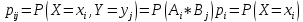 ,
, 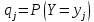
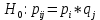
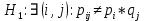
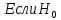 верна:
верна: 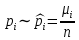
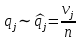
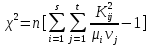 . В случае s = t = 2:
. В случае s = t = 2: 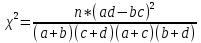
| X | Y | |
| B1 | B2 | |
| A1 | a | b |
| A2 | c | d |
Критическая область
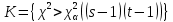 .
.Сформулируйте определение асимптотически нормальной оценки и приведите пример такой оценки (с доказательством).
Асимптотически нормальная оценка — оценка, распределение которой стремится к нормальному при увеличении размера выборки. Пусть
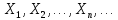 {\displaystyle X_{1},\ldots ,X_{n},\ldots } — выборка из распределения {\displaystyle \mathbb {P} _{\theta }}
{\displaystyle X_{1},\ldots ,X_{n},\ldots } — выборка из распределения {\displaystyle \mathbb {P} _{\theta }}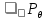 , зависящего от параметра
, зависящего от параметра 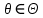 {\displaystyle \theta \in \Theta }
{\displaystyle \theta \in \Theta }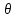 . Точечная оценка {\displaystyle {\hat {\theta }}}
. Точечная оценка {\displaystyle {\hat {\theta }}}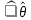 называется асимптотически нормальной с дисперсией {\displaystyle \sigma \ ^{2}(\theta )}
называется асимптотически нормальной с дисперсией {\displaystyle \sigma \ ^{2}(\theta )}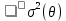 , если{\displaystyle {\sqrt {n}}\left({\hat {\theta }}-\theta \right)\to Z}
, если{\displaystyle {\sqrt {n}}\left({\hat {\theta }}-\theta \right)\to Z} 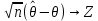 по распределению при
по распределению при 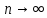 {\displaystyle n\to \infty }, где
{\displaystyle n\to \infty }, где 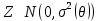 – нормальная случайная величина.
– нормальная случайная величина.Пример:
Пусть
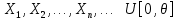 – выборка из непрерывного равномерного распределения, где
– выборка из непрерывного равномерного распределения, где 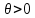 . Пусть
. Пусть 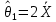 , где
, где 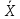 – выборочное среднее, а
– выборочное среднее, а 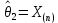 , где
, где 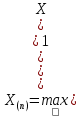 . Можно заметить, что первая оценка является асимптотически нормальной с дисперсией
. Можно заметить, что первая оценка является асимптотически нормальной с дисперсией 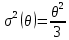 , а вторая – нет. {\displaystyle X_{1},\ldots ,X_{n},\ldots } {\displaystyle Z\sim \mathrm {N} \left(0,\sigma ^{2}(\theta )\right)}
, а вторая – нет. {\displaystyle X_{1},\ldots ,X_{n},\ldots } {\displaystyle Z\sim \mathrm {N} \left(0,\sigma ^{2}(\theta )\right)}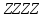

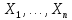 ) – выборка из N(
) – выборка из N(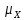 ,
, 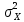 ), а
), а 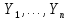 )– выборка из нормального распределения N(
)– выборка из нормального распределения N(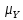 ,
, 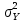 ). Выборки X и Y независимы. Известны их дисперсии
). Выборки X и Y независимы. Известны их дисперсии 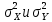 .
. 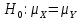 .
.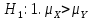 , 2.
, 2.