КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Исследование операций». Исследование операций

• Название: Исследование операций
• Анкор: КОНТРОЛЬНАЯ РАБОТА по дисциплине: «Исследование операций
• Дата: 20.10.2021
• Размер: 131 Kb.
• Имя файла: Kontrolnaya.doc
• Тип: Исследование; #252186

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования

«Владимирский государственный университет
имени Александра Григорьевича и Николая Григорьевича Столетовых»

 

 

 
 

КОНТРОЛЬНАЯ РАБОТА

по дисциплине:

«Исследование операций»


Выполнил студент::

Группы: ЗПИуд-216

Кожевников И.И.

Владимир 2018 г.


Контрольная работа № 1

Задание 1. Имеется множество новых продуктов Р1,Р2,Р3 и относительные оценки эффективности их выпуска S1,S2,S3. Требуется, используя минимаксный критерий определить наилучший продукт

	P1	P2	P3
S1	0,25	0,35	0,4
S2	0,75	0,2	0,3
S3	0,35	0,8	0,1
S4	0,9	0,2	0,3
min	0,25	0,2	0,1
max	0,25

Решение:

Критерий максимакса.

Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.

Ai	П1	П2	П3	max(aij)
A1	0.25	0.35	0.4	0.4
A2	0.75	0.2	0.3	0.75
A3	0.35	0.8	0.1	0.8
A4	0.9	0.2	0.3	0.9

Выбираем из (0.4; 0.75; 0.8; 0.9) максимальный элемент max=0.9

Вывод: выбираем стратегию N=4.

Критерий Севиджа.

Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:

a = min(max r_ij)

Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

Находим матрицу рисков.

Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.

1. Расчитываем 1-й столбец матрицы рисков.

r₁₁ = 0.9 - 0.25 = 0.65; r₂₁ = 0.9 - 0.75 = 0.15; r₃₁ = 0.9 - 0.35 = 0.55; r₄₁ = 0.9 - 0.9 = 0;

2. Расчитываем 2-й столбец матрицы рисков.

r₁₂ = 0.8 - 0.35 = 0.45; r₂₂ = 0.8 - 0.2 = 0.6; r₃₂ = 0.8 - 0.8 = 0; r₄₂ = 0.8 - 0.2 = 0.6;

3. Расчитываем 3-й столбец матрицы рисков.

r₁₃ = 0.4 - 0.4 = 0; r₂₃ = 0.4 - 0.3 = 0.1; r₃₃ = 0.4 - 0.1 = 0.3; r₄₃ = 0.4 - 0.3 = 0.1;

Ai	П1	П2	П3
A1	0.65	0.45	0
A2	0.15	0.6	0.1
A3	0.55	0	0.3
A4	0	0.6	0.1

Результаты вычислений оформим в виде таблицы.

Ai	П1	П2	П3	max(aij)
A1	0.65	0.45	0	0.65
A2	0.15	0.6	0.1	0.6
A3	0.55	0	0.3	0.55
A4	0	0.6	0.1	0.6

Выбираем из (0.65; 0.6; 0.55; 0.6) минимальный элемент min=0.55

Вывод: выбираем стратегию N=3.

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₃.

Задание 2. В ряде экономических задач в качестве критерия эффективности принимаемых решений выступает показатель минимума затрат.

.

В качестве затрат могут выступать:

- капиталовложения;

- валовые издержки производства;

- приведенные годовые затраты и т.д.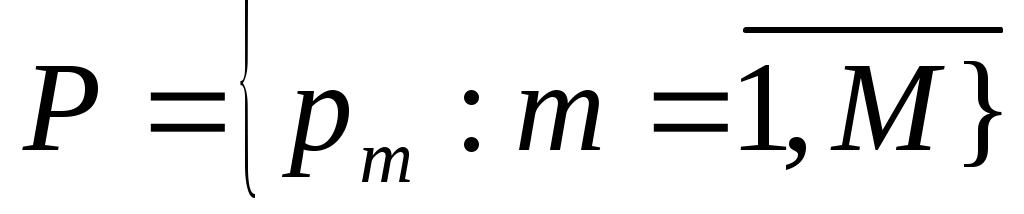

- множество производственных программ;

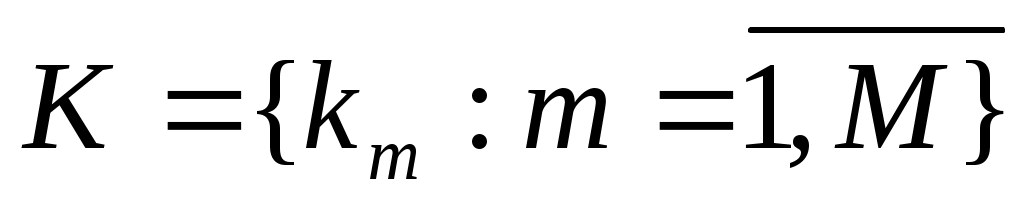- капиталовложения в производственные программы.

Величины являются управляемыми ( контролируемыми ) факторами.

Каждой программе соответствует определенное значение себестоимости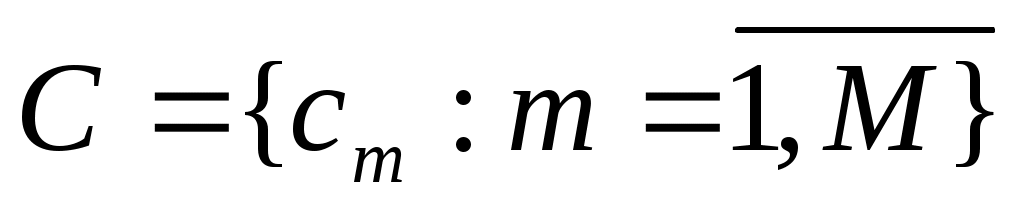

, , - нормативный коэффициент эффективности капиталовложений.

Используя ММ- критерий найти наилучшее решение, оптимистическое и пессимистическое решения

	C1	C2	C3	C4
k1	100	130	75
k2	80	200	140
k3	60	180	200
k4	130	90	150
	Критерий пессимизма
	Критерий оптимизма

Решение:

Критерий максимакса.

Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации.

Ai	П1	П2	П3	max(aij)
A1	100	130	75	130
A2	80	200	140	200
A3	60	180	200	200
A4	130	90	150	150

Выбираем из (130; 200; 200; 150) максимальный элемент max=200

Вывод: выбираем стратегию N=2.

Критерий Севиджа.

Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:

a = min(max r_ij)

Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.

Находим матрицу рисков.

Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце b_j = max(a_ij) характеризует благоприятность состояния природы.

1. Расчитываем 1-й столбец матрицы рисков.

r₁₁ = 130 - 100 = 30; r₂₁ = 130 - 80 = 50; r₃₁ = 130 - 60 = 70; r₄₁ = 130 - 130 = 0;

2. Расчитываем 2-й столбец матрицы рисков.

r₁₂ = 200 - 130 = 70; r₂₂ = 200 - 200 = 0; r₃₂ = 200 - 180 = 20; r₄₂ = 200 - 90 = 110;

3. Расчитываем 3-й столбец матрицы рисков.

r₁₃ = 200 - 75 = 125; r₂₃ = 200 - 140 = 60; r₃₃ = 200 - 200 = 0; r₄₃ = 200 - 150 = 50;

Ai	П1	П2	П3
A1	30	70	125
A2	50	0	60
A3	70	20	0
A4	0	110	50

Результаты вычислений оформим в виде таблицы.

Ai	П1	П2	П3	max(aij)
A1	30	70	125	125
A2	50	0	60	60
A3	70	20	0	70
A4	0	110	50	110

Выбираем из (125; 60; 70; 110) минимальный элемент min=60

Вывод: выбираем стратегию N=2.

Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A₂.

Контрольная работа № 2

Задание 1.Компания производит продукцию определенного ассортимента и осуществляет сбыт по четырем каналам:

1. 
   ежемесячный объем продукции с устойчивыми связями по сбыту на ряд лет в среднем -490000 руб.;
   
2. 
   ежемесячный объем продукции с устойчивым сбытом. Но не на длительный срок -500000 руб.;
   
3. 
   ежемесячный объем продукции. Обеспеченный только разовыми покупками 510000 руб.;
   
4. 
   месячная продукция, покупатель на которую не определен- 480000 руб.
   

Компания может осуществлять производство продукции по трем проектам в объемах 980000,1500000,1980000 руб.

В зависимости от изменений рыночной конъюнктуры в связи с имеющимися возможностями реализации рассчитать, используя ММ-критерий, варианты среднегодовой прибыли.

		Прибыль
	П1	П2	П3	П4
Р1=980000	49300	197200	197200	197200
Р2=1500000	-60	148900	297800	297800
Р3=1980000	-1140	98400	196800	395600
Решение: Критерий максимакса. Критерий максимакса ориентирует статистику на самые благоприятные состояния природы, т.е. этот критерий выражает оптимистическую оценку ситуации. Ai П1 П2 П3 П4 max(aij) A1 49300 197200 197200 197200 197200 A2 -60 148900 297800 297800 297800 A3 -1140 98400 196800 395600 395600 Выбираем из (197200; 297800; 395600) максимальный элемент max=395600 Вывод: выбираем стратегию N=3. Критерий Севиджа. Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается: a = min(max rij) Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации. Находим матрицу рисков. Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы. 1. Расчитываем 1-й столбец матрицы рисков. r11 = 49300 - 49300 = 0; r21 = 49300 - (-60) = 49360; r31 = 49300 - (-1140) = 50440; 2. Расчитываем 2-й столбец матрицы рисков. r12 = 197200 - 197200 = 0; r22 = 197200 - 148900 = 48300; r32 = 197200 - 98400 = 98800; 3. Расчитываем 3-й столбец матрицы рисков. r13 = 297800 - 197200 = 100600; r23 = 297800 - 297800 = 0; r33 = 297800 - 196800 = 101000; 4. Расчитываем 4-й столбец матрицы рисков. r14 = 395600 - 197200 = 198400; r24 = 395600 - 297800 = 97800; r34 = 395600 - 395600 = 0; Ai П1 П2 П3 П4 A1 0 0 100600 198400 A2 49360 48300 0 97800 A3 50440 98800 101000 0 Результаты вычислений оформим в виде таблицы. Ai П1 П2 П3 П4 max(aij) A1 0 0 100600 198400 198400 A2 49360 48300 0 97800 97800 A3 50440 98800 101000 0 101000 Выбираем из (198400; 97800; 101000) минимальный элемент min=97800 Вывод: выбираем стратегию N=2. Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A2. Задание 2
Используя данные заданий 1-3. Контрольной работы 1, и задания1 контрольной работы 2 провести расчеты для критерия Сэвиджа
Решение: см. в каждой задаче

Контрольная работа № 3.

Задание1. Игра задана платежной матрицей

	Y1	Y2	A(x)
X1	3	6
X2	5	4
B(y)

Определить оптимальные чисты стратегии игроков.

Решение:

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	a = min(Ai)
A1	3	6	3
A2	5	4	4
b = max(Bi)	5	6	0

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = 4, которая указывает на максимальную чистую стратегию A₂.

Верхняя цена игры b = min(b_j) = 5.

Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 4 ≤ y ≤ 5. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).

2. Проверяем платежную матрицу на доминирующие строки и доминирующие столбцы.

Иногда на основании простого рассмотрения матрицы игры можно сказать, что некоторые чистые стратегии могут войти в оптимальную смешанную стратегию лишь с нулевой вероятностью.

Говорят, что i-я стратегия 1-го игрока доминирует его k-ю стратегию, если a_ij ≥ a_kj для всех j Э N и хотя бы для одного j a_ij > a_kj. В этом случае говорят также, что i-я стратегия (или строка) – доминирующая, k-я – доминируемая.

Говорят, что j-я стратегия 2-го игрока доминирует его l-ю стратегию, если для всех j Э M a_ij ≤ a_il и хотя бы для одного i a_ij < a_il. В этом случае j-ю стратегию (столбец) называют доминирующей, l-ю – доминируемой.

В платежной матрице отсутствуют доминирующие строки.

В платежной матрице отсутствуют доминирующие столбцы.

Так как игроки выбирают свои чистые стратегии случайным образом, то выигрыш игрока I будет случайной величиной. В этом случае игрок I должен выбрать свои смешанные стратегии так, чтобы получитьмаксимальный средний выигрыш.

Аналогично, игрок II должен выбрать свои смешанные стратегии так, чтобы минимизировать математическое ожидание игрока I.

3. Находим решение игры в смешанных стратегиях.

Запишем систему уравнений.

Для игрока I

3p₁+5p₂ = y

6p₁+4p₂ = y

p₁+p₂ = 1

Для игрока II

3q₁+6q₂ = y

5q₁+4q₂ = y

q₁+q₂ = 1

Решая эти системы методом Гаусса, находим:

y = 4¹/₂

p₁ = ¹/₄ (вероятность применения 1-ой стратегии).

p₂ = ³/₄ (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока I: P = (¹/₄; ³/₄)

q₁ = ¹/₂ (вероятность применения 1-ой стратегии).

q₂ = ¹/₂ (вероятность применения 2-ой стратегии).

Оптимальная смешанная стратегия игрока II: Q = (¹/₂; ¹/₂)

Цена игры

y = 4¹/₂

Задание 2. Игра задана платежной матрицей. Найти оптимальные смешанные стратегии игроков

	Х1	Х2	Х3	Х4	min
У1	0	5	6	-4	-4
У2	3	9	9	-6	-6
У3	3	-1	2	0	-1
max	3	9	9	2

Решение:

Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.

Игроки	B1	B2	B3	B4	a = min(Ai)
A1	0	5	6	-4	-4
A2	3	9	9	-6	-6
A3	3	-1	2	-1	-1
b = max(Bi )	3	9	9	-1	0

Находим гарантированный выигрыш, определяемый нижней ценой игры a = max(a_i) = -1, которая указывает на максимальную чистую стратегию A₃.

Верхняя цена игры b = min(b_j) = -1.

Седловая точка (3, 4) указывает решение на пару альтернатив (A3,B4).

Цена игры равна -1.