ТОЭ 6. Исследование параметров катушек индуктивности
 Скачать 197.5 Kb.
|
|
МИНОБРНАУКИ РОССИИ САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ЭЛЕКТРОТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ «ЛЭТИ» ИМ. В.И. УЛЬЯНОВА (ЛЕНИНА) ОТЧЕТ по лабораторной работе №6 по дисциплине «Компоненты электронной техники » Тема: Исследование параметров катушек индуктивности Студенты гр. 5802 Лакиза И.С. Лапин О.И. Преподаватель Староверов Н.Е. Санкт-Петербург 2017 Исследование параметров катушек индуктивности Цель работы – ознакомление с основными параметрами катушек индуктивности и методами их измерений. Движущиеся заряды (токи) порождают магнитное поле.  где  Гн/м – магнитная проницаемость вакуума (воздуха); μ – относительная магнитная проницаемость вещества по отношению к вакууму; B - электромагнитная индукция; Магнитное поле удается сконцентрировать внутри катушки, образованной множеством близко расположенных витков с током I. Если принять, что все составляющие индукции по сечению катушки S равны некоторому среднему значению В, что справедливо для катушек с сердечником, то отдельные значения В суммируются в полный поток электромагнитной индукции, или магнитный поток, определяемый как = ВS = LI, (1) где L – коэффициент пропорциональности между током и полным магнитным потоком катушки, называемый индуктивностью катушки. Индуктивность зависит от геометрии катушки, от магнитной проницаемости сердечника и от магнитных свойств окружающей среды. Так, для дросселей с замкнутыми тороидальными магнитопроводами индуктивность определяется формулой 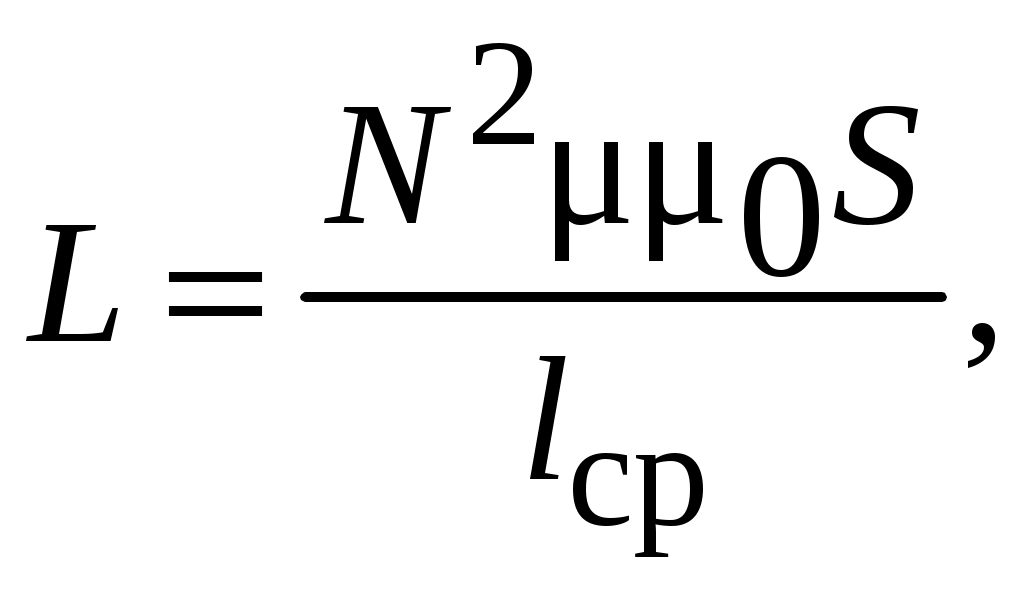 (2)где N– количество витков; S – сечение магнитопровода;  – средняя длина окружности, определяемая как полусумма длин окружностей внутреннего и внешнего контуров магнитопровода. В данной работе используется сердечник с μ = 2000, = 26 мм, S= 108 мм2.Единицей индуктивности является генри [Гн]. Одному генри соответствует индуктивность катушки без сердечника, которая развивает поток электромагнитной индукции в 1 Вб (вебер) в результате протекания тока 1 А. В соответствии с законом Ленца изменение магнитного потока Ф, пронизывающего замкнутый контур, порождает в нем возникновение индуцированной ЭДС (Е):  (3)ЭДС катушки индуктивности при изменении протекающего через нее тока  Из (3) следует, что включение индуктивности последовательно с цепью нагрузки, питаемой от пульсирующего источника тока, снижает его пульсации за счет возникающей ЭДС самоиндукции. Если индуктивность не зависит от тока и в других элементах цепи никаких изменений не происходит, остается заключить, что магнитное поле является носителем энергии, за счет которой и совершается данная работа. Таким образом, катушка с индуктивностью L, через которую протекает ток I, запасает энергию 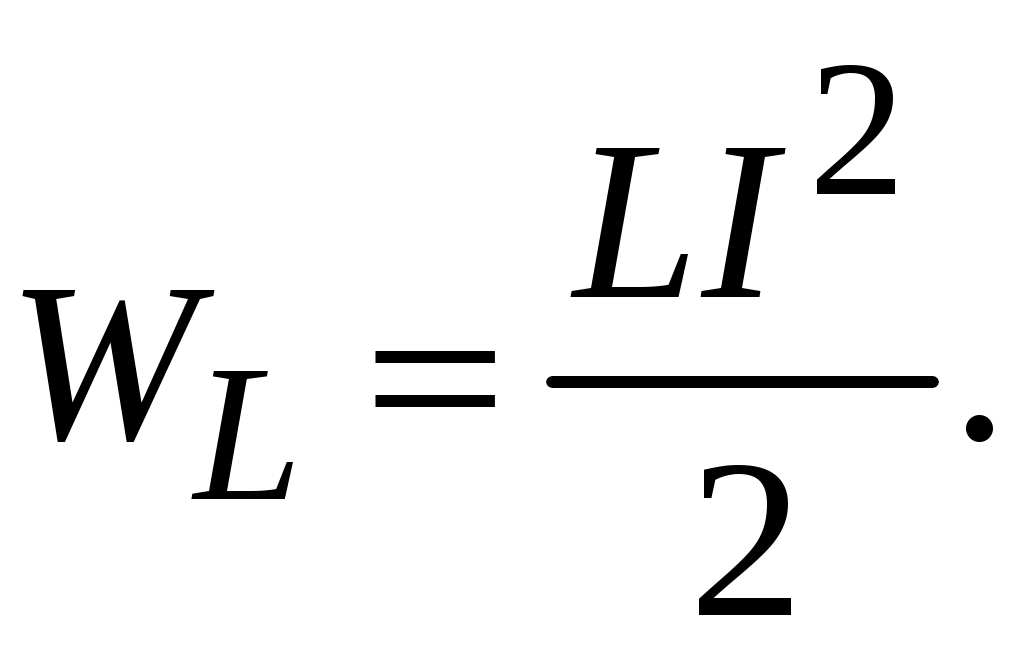 равную (4)Катушка не может запасти энергию мгновенно. Ее нужно зарядить аналогично тому, как заряжают конденсатор. Если индуктивность подключается к источнику постоянного напряжения (U), то ее зарядка происходит по экспоненциальному закону: 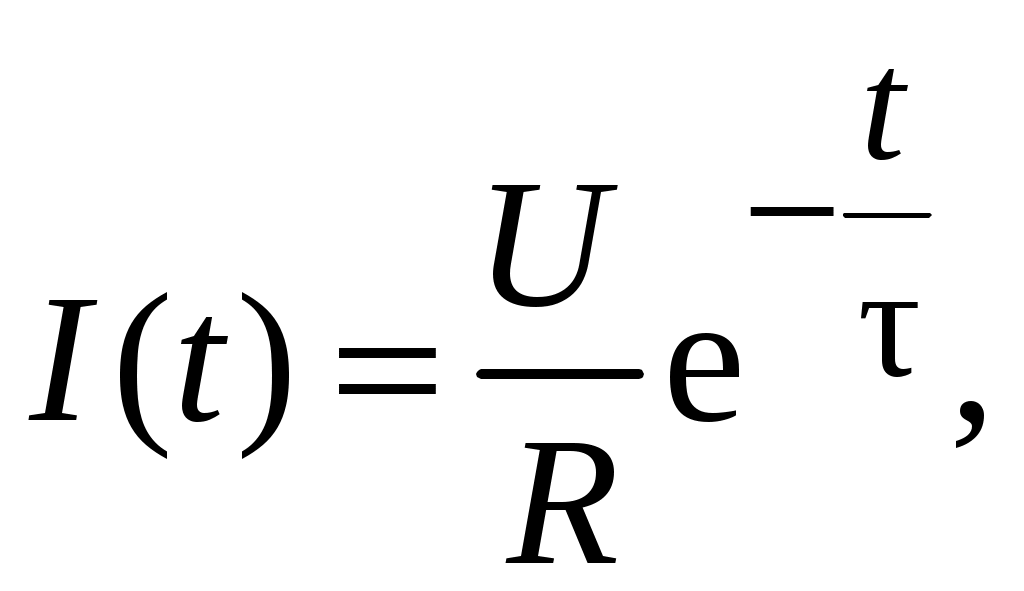 где R – полное активное сопротивление, ограничивающее ток индуктивности; τ = L/R – постоянная времени зарядки индуктивности. Цепь, состоящую из катушки индуктивности и параллельно подключенного ей конденсатора, называют колебательным контуром. При работе индуктивности в составе колебательного контура, ее периодическая зарядка и разрядка происходят на резонансной частоте контура: 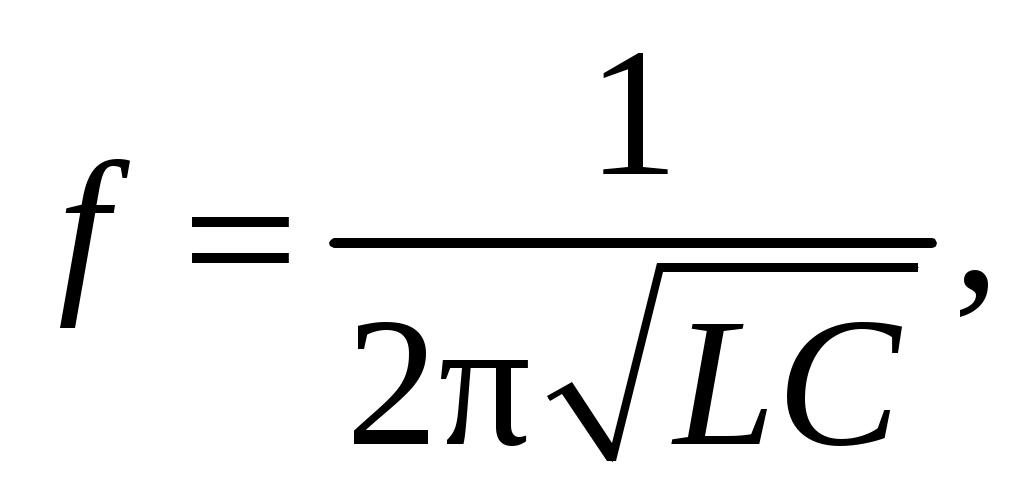 (5)где С – емкость конденсатора, входящего в колебательный контур. В колебательном контуре происходит периодическое превращение энергии, запасенной в катушке индуктивности, в энергию заряженного конденсатора: 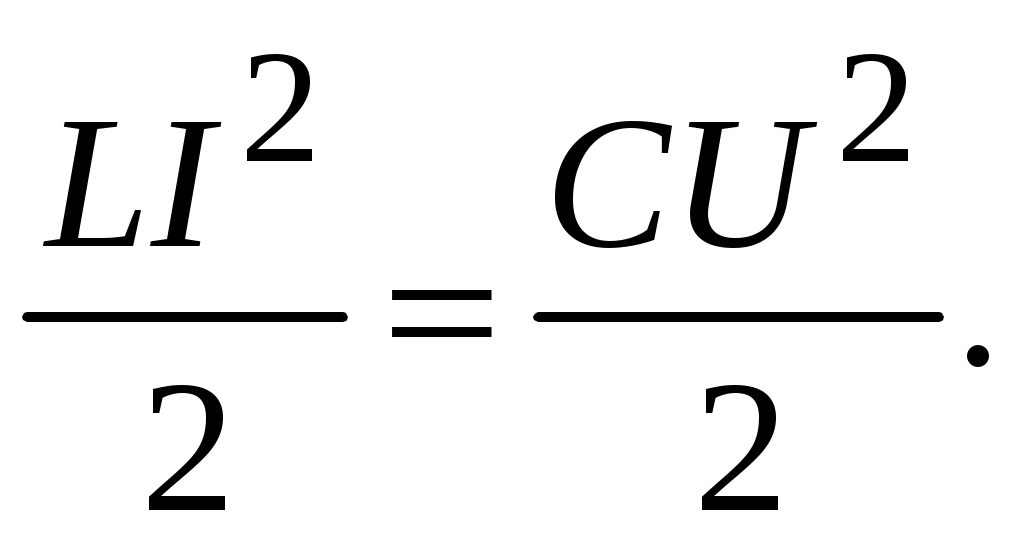 (6)Ток обусловлен совместным влиянием активного и реактивного сопротивлений цепи: 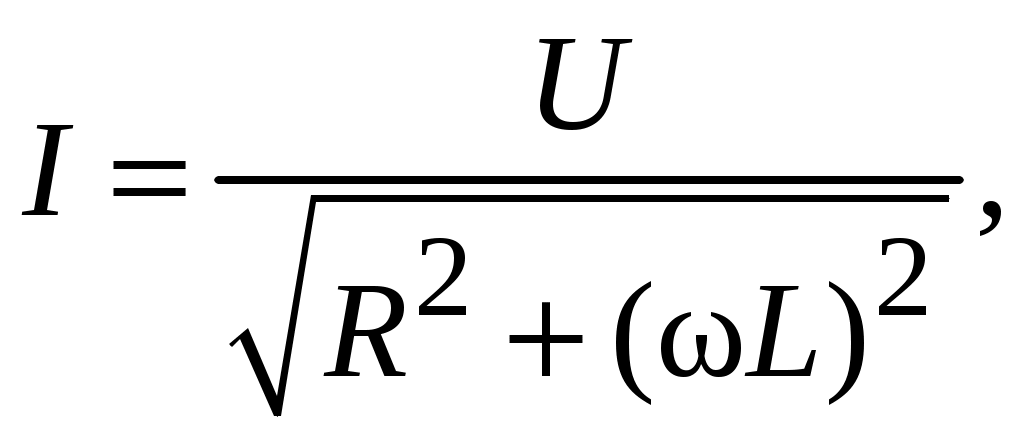 (7)где ω = 2πf – угловая частота. Если индуктивность катушки невелика, то используется резонансный метод, в котором параллельно индуктивности устанавливают конденсатор с известной емкостью и измеряют частоту резонанса образованного колебательного контура. Протокол Измерение индуктивности низкочастотного дросселя R=34 Oм.
Таб. 1 Измерение индуктивности низкочастотного дросселя R=2,9 Ом С=68 нФ UВК=10В
Таб. 2 Измерение индуктивности и энергии, запасаемой в высокочастотном дросселе Расчетная часть 1 )Расчет индуктивности низкочастотного дросселя для двух исследованных режимов  (1) (2)  2) Расчет индуктивности и высокочастотного дросселя для двух исследованных режимов. Рассчитанное значение энергии, сообщаемой от дросселя конденсатору в колебательном контуре. 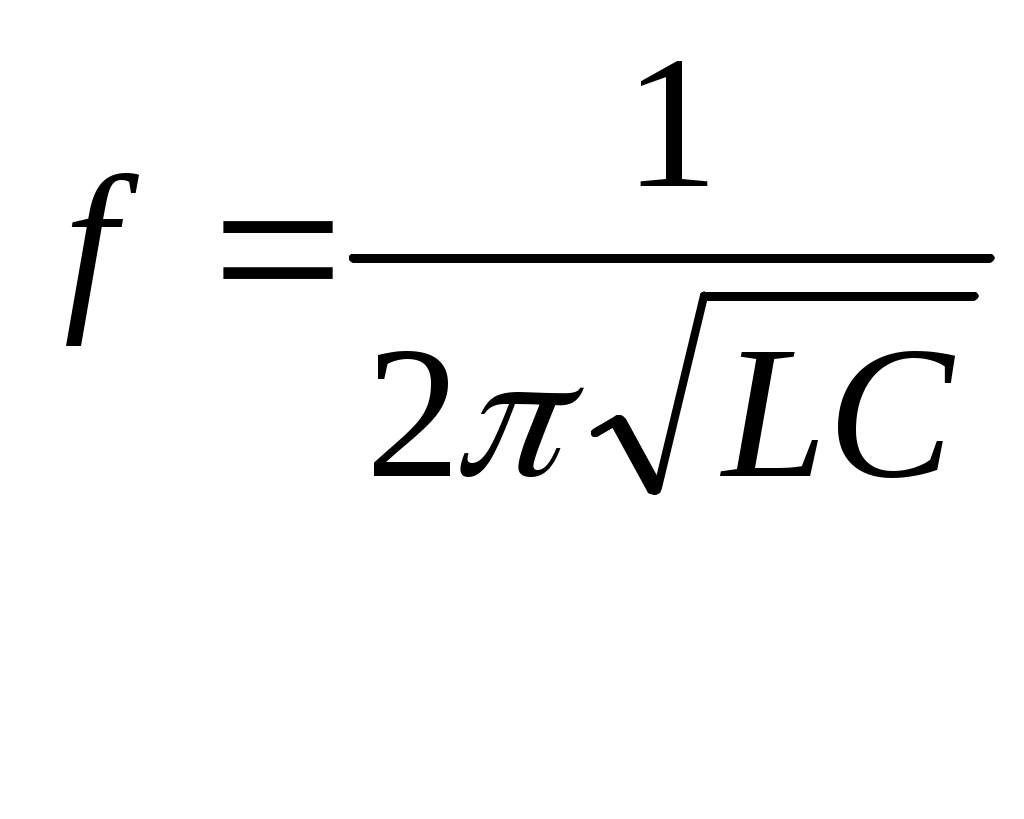 (3)    (4)    
Таб. 3   =4,1*10-6 Гн.
Таб.4 Теоретический и экспериментальный графики зависимости индуктивности от количества витков 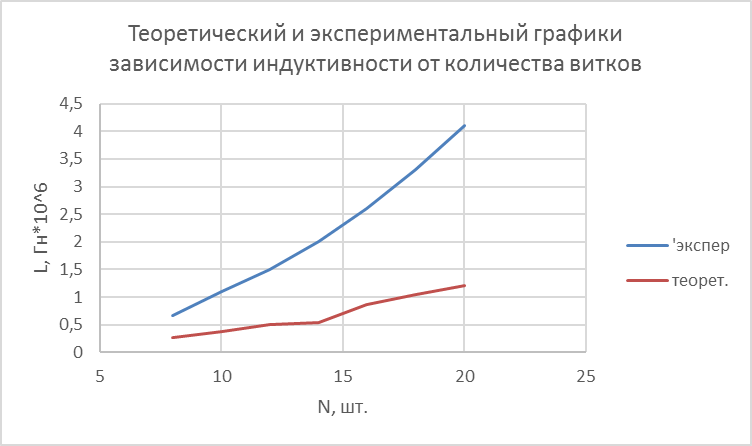 Вывод Были рассчитаны индуктивности низкочастотного дросселя при разных напряжениях. Данные разнятся. Расчеты сообщаемой энергии и энергии запасаемой говорит о том, что больше половины энергии, сообщаемой от дросселя конденсатору, запасается. |