ТОЭ2 4 варик. Исследование переходных процессов в r l цепи
 Скачать 291.88 Kb. Скачать 291.88 Kb.
|
|
Некоммерческое акционерное общество «АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ» имени Гумарбека Даукеева Кафедра Электротехники TOE (II) 2216 – Теоретические основы электротехники 2 по образовательной программе 6В07101 – Электроэнергетика ОТЧЕТ по лабораторной работе № 2 На тему «Исследование переходных процессов в RL-цепи» Выполнил Есенгазин Тамирлан Группа ЭЭ-20-14 (Ф.И.О. студента) Принял ст. преподавательь кафедры ТОЭ Баймаганов А.С (ученая степень, звание, Ф.И.О.) ____________ ________________ «02» 03 2022г. (оценка) (подпись) Алматы 2022 Лабораторная работа № 2. Исследование переходных процессов в RL-цепиЦель работы: получение навыков экспериментального исследования переходных процессов в цепи с одним накопителем энергии. Подготовка к работПовторить раздел курса ТОЭ2 «Переходные процессы в RC-цепях». Ответить на вопросы и выполнить следующее: Что такое переходные процессы и в результате чего они возникают? В каких цепях имеют место переходные процессы? Переходные процессы - процессы возникающие в электрических цепях при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, то есть, - при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии и т. д. Физическая причина возникновения переходных процессов в цепях - наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и ёмкостных элементов в соответствующих схемах замещения. Записать закон коммутации для цепей, содержащих конденсатор. I закон коммутации: ток в индуктивности до коммутации равен току в индуктивности в начальный момент после коммутации 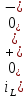 II закон коммутации: напряжение на емкости до коммутации равно напряжению на емкости в начальный момент после коммутации 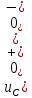 Что называют принуждённой и свободной составляющими переходных токов и напряжений? Переходный ток – электрический ток в электрической цепи во время переходного процесса. Принужденный ток представляет собой ток в цепи батареи при установившееся режиме. Свободный ток – электрический ток, возникающий в электрической цепи вследствие несоответствия кол-ва электромагнитной энергии, имеющейся в участках цепи к начальному моменту переходного процесса. Каков физический смысл постоянной времени цепи? Чему равна постоянная времени RC-цепи? Как экспериментально определить постоянную времени цепи? В общем случае постоянная времени определяет длительность переходного процесса. За время t=3τ ток или напряжение достигают 95% от установившегося значения. За время t=5τ переходной процесс считается законченным. Постоянная времени для RL -цепи L/R=τ Чем больше индуктивность цепи и меньше ее сопротивление, тем больше постоянная времени и дольше устанавливается или уменьшается ток. Постоянная времени для RC -цепи RC=τ Чем больше емкость цепи, тем больше времени потребуется для заряда-разряда конденсатора, т.е. длиннее переходной процесс. Какова продолжительность переходного процесса теоретически и на практике? Что называют коэффициентом затухания цепи? Коэффициентом затухания называют физическую величину, показывающую размер (величину) затухания на единицу длины пути, зависящий от структуры, параметров и свойств среды, длин и типов волн и др. Привести выражения, соответствующие переходным напряжению uC(t) и току iC(t) при коротком замыкании RC-цепи, начертить их графики. Порядок выполнения работы на стенде в лабораторииСобрать цепь (рисунок 2.1). На рисунке использованы обозначения: ЭК – электронный ключ, Rк – активное сопротивление катушки индуктивности.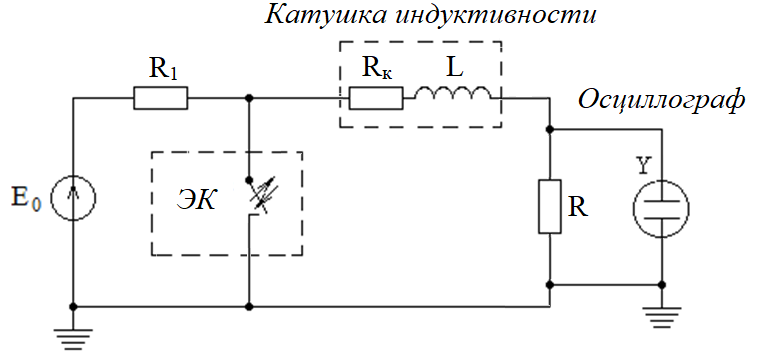 Рисунок 2.1 – Схема для исследования RL-цепи Опыт 1, установить значения E0 и L согласно варианту (таблица 2.1), R1 = 50 Ом, R = 5 Ом, измерить омметром активное сопротивление катушки индуктивности Rк, фактические параметры цепи записать в таблицу 2.2.На вход осциллографа подать напряжение с резистора R, срисовать с экрана осциллографа в масштабе кривую напряжения uR(t), соответствующую режиму разряда индуктивности, то есть при замыкании ключа. Эта кривая представляет собой кривую тока в соответствующем масштабе: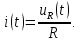 На вход осциллографа подать напряжение с катушки индуктивности, срисовать в масштабе полученную кривую uк(t). В случае, если пренебречь активным сопротивлением катушки Rк, можно считать, что uк(t) = uL(t).Опыт 2, изменить, согласно варианту, значение индуктивности L (таблица 2.1), фактические параметры цепи записать в таблицу 2.2. Срисовать в масштабе новую кривую напряжения uR(t) при разряде индуктивности.Таблица 2.1 – Параметры RL- цепи для первого и второго опытов
Таблица 2.2 – Фактические параметры RL-цепи
Порядок выполнения работы в приложении EWBСобрать цепь, состоящую из последовательно соединённых резистора и индуктивности. На вход подать напряжение с функционального генератора и выбрать на генераторе прямоугольную форму сигнала. Подключить осциллограф параллельно резистору (рисунок 2.2).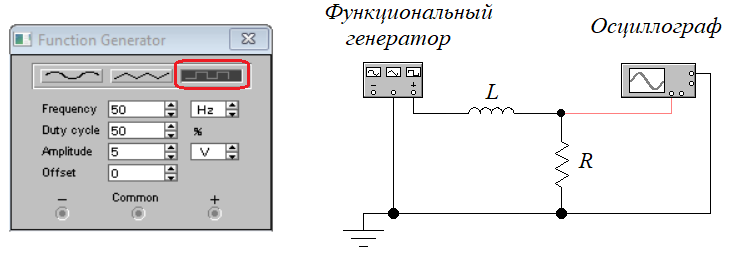 Рисунок 2.2 – Схема для исследования RL-цепи (EWB) Опыт 1, установить значения R и L согласно варианту (таблица 2.1). На генераторе выставить значения частоты f = 50 Гц и амплитуды входного напряжения E0 согласно варианту задания (таблица 2.1).На вход осциллографа подать напряжение с резистора R, срисовать с экрана осциллографа в масштабе полученную кривую uR(t). Эта кривая представляет собой кривую тока в соответствующем масштабе: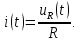 На вход осциллографа подать напряжение с индуктивности, срисовать в масштабе полученную кривую uL(t).Опыт 2, изменить, согласно варианту, индуктивность L (таблица 2.1), фактические параметры цепи записать в таблицу 2.2. Срисовать в масштабе новую кривую напряжения uR(t).Оформление и анализ результатов работыРассчитать теоретические значения постоянных времени цепи первого и второго опытов 1теор. и 2теор., а также коэффициентов затухания 1теор. и 2теор., используя фактические значения параметров цепи (таблица 2.2), сравнить их, проанализировать влияние величины индуктивности L на постоянную времени цепи и соответственно на скорость протекания переходного процесса, определить время разряда индуктивности, с точностью до 1% (4,6).Примечание: при выполнении экспериментальной части работы на стенде в лаборатории необходимо учитывать общее сопротивление RL-цепи при замкнутом электронном ключе R∑ = R+Rк. По изображению кривых напряжения на резисторе uR(t) (фактически по кривой тока) в первом и во втором опытах определить экспериментальные значения постоянных времени 1эксп. и 2эксп., а также коэффициентов затухания 1эксп. и 2эксп. Сравнить полученные значения с теоретическими, сделать вывод.Рассчитать законы изменения тока в индуктивности iL(t) и напряжений uL(t) и uR(t) на основе фактических параметров цепи в первом опыте.Расчётную и экспериментальную зависимости первого опыта кривых напряжения uR(t) привести на одном графике.Расчётную и экспериментальную зависимости первого опыта кривых напряжения uL(t) привести на одном графике.Примечание: при выполнении экспериментальной части работы на стенде в лаборатории необходимо учитывать, что напряжение на катушке индуктивности, согласно схеме замещения, представляет собой сумму напряжений на её активном сопротивлении и индуктивности uк(t) = uRк(t) + uL(t). Таким образом, экспериментальная кривая напряжения на индуктивности катушки uL(t) получается графически согласно выражению: 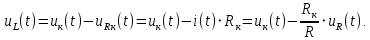 Методические указания.Масштаб по оси времени определяется из условия, что электронный ключ (ЭК) замыкается и размыкается с частотой f = 50 Гц и с периодом: 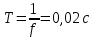 . .Экспериментальное значение постоянной времени цепи эксп. определяется как подкасательная по кривой напряжения uR(t), полученной с помощью осциллографа (рисунок 1.3). Интервал замкнутого состояния ЭК равен 10 мс. 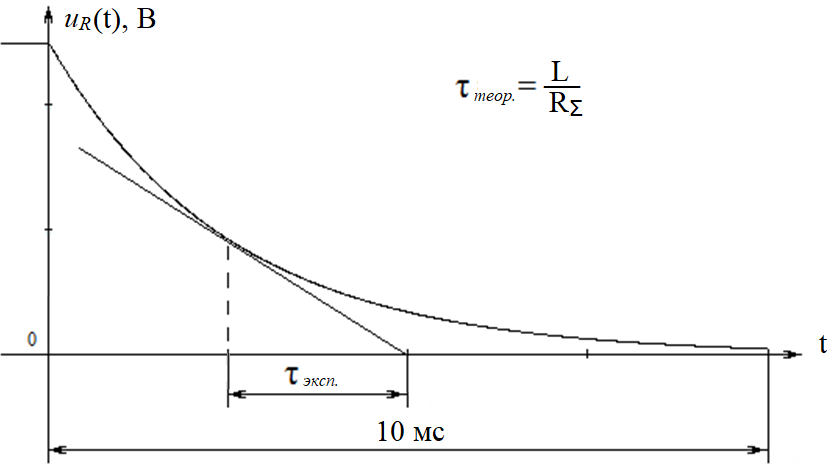 Рисунок 2.3 – Определение постоянной времени цепи по кривой uR1(t) Обработка результатов экспериментов: Для начала соберем схему в Electronic Workbench вставив в нее данные согласно моему варианту(Рисунок1) 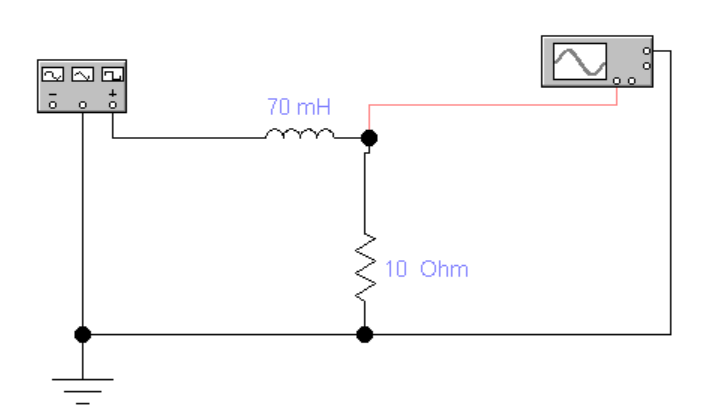 Рисунок1-Схема цепи RL при 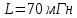 в EWB в EWBУстановил значения Uвх, R и L согласно варианту (таблица 1.1): 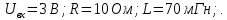 После я зафиксировал полученную кривую на осциллографе (Рисунок2): 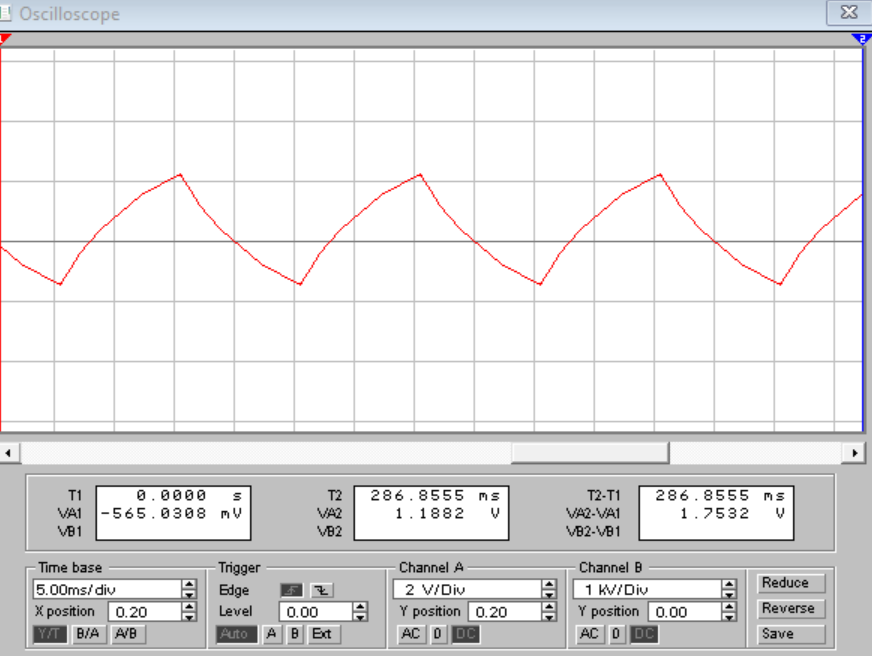 Рисунок 2-кривая осциллографа цепи RL при 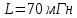 в EWB в EWBПосле повторил опыт 2, суть которого заключалась в том чтобы изменить согласно варианту один из параметров цепи (таблица 1.2), срисовать в масштабе новую кривую напряжения uR(t). Установил значения Uвх, R и L согласно варианту (таблица 2.1): 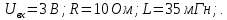 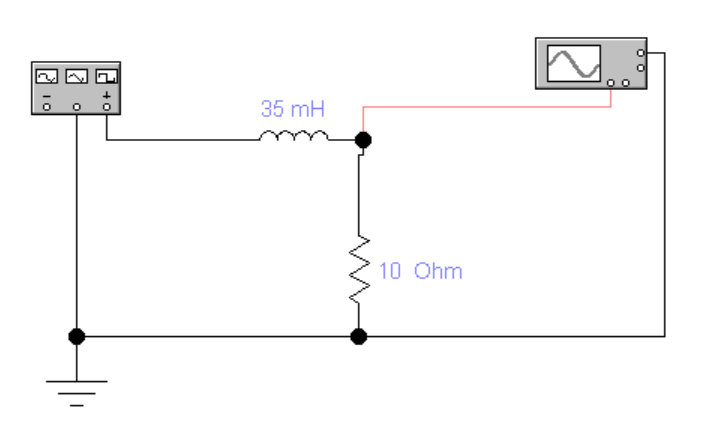 Рисунок-Схема цепи RL при 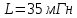 в EWB в EWBУстановил значения Uвх, R и L согласно варианту (таблица 1.1): 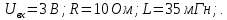 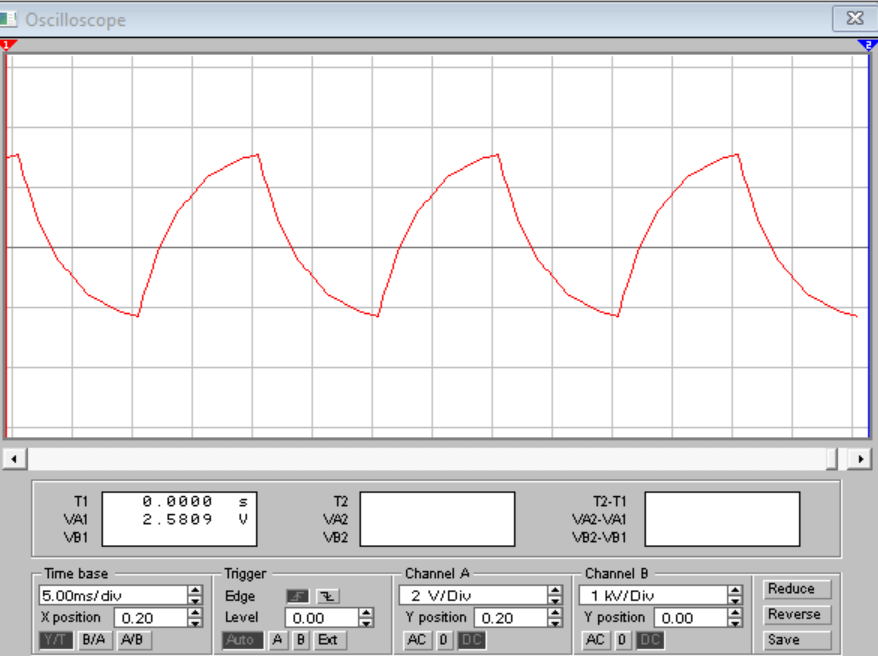 Рисунок -кривая осциллографа цепи RL при 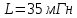 в EWB в EWBТеперь нужно Рассчитать постоянную времени С1 и коэффициент затухания цепи С1 для параметров цепи согласно заданному варианту (таблица 2.1) и С2, С2 согласно варианту (таблица 2.2). По изображению кривой напряжения uC(t) определил постоянную времени С1 и коэффициент затухания цепи Расчетная часть: Опыт 1 При 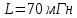 : :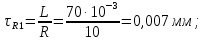 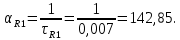 Экспериментальная часть: 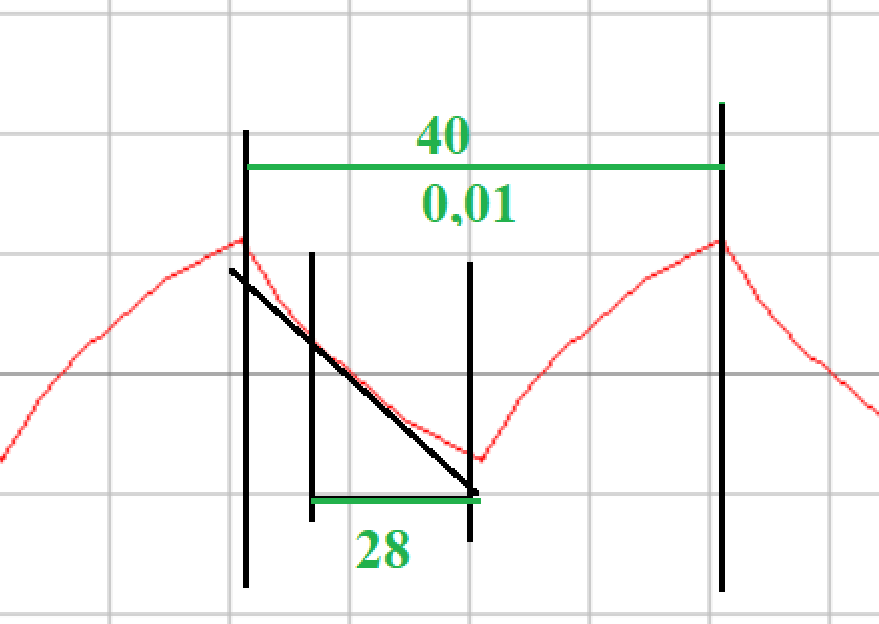 Составил пропорцию по рисунку и рассчитал 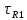 и и 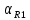 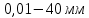 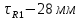 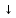 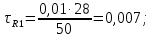 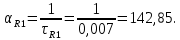 Расчетная часть: Опыт 2 При 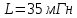 : :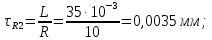 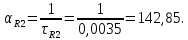 Экспериментальная часть: 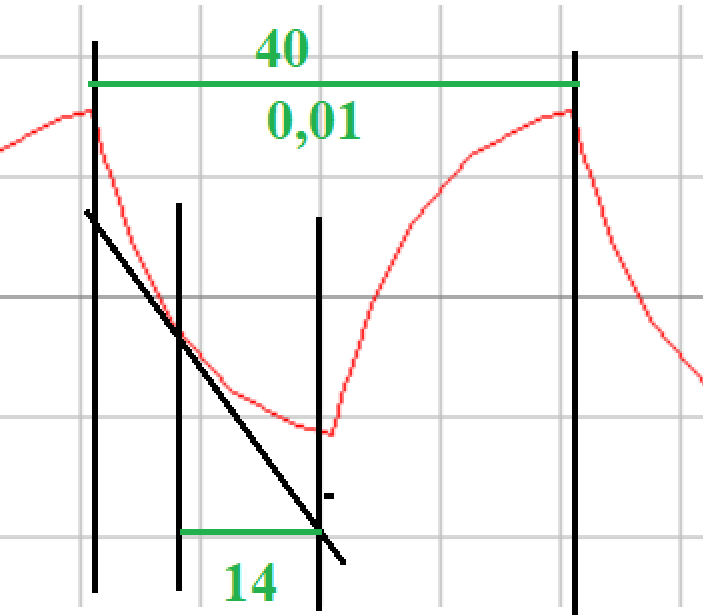 Составил пропорцию по рисунку и рассчитал 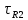 и и 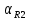 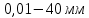 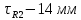  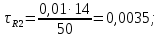 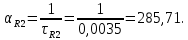 Сопротивления индуктивностей и ёмкостей принимаются равными комплексным сопротивлениям при синусоидальном токе, в которых произведение jωзаменяют на оператор p. Сопротивление индуктивности равно pL, а сопротивление ёмкости 1/pC. Затем разрывают одну из ветвей в полученной пассивной цепи, записывают входное сопротивление Z(p) относительно выводов разрыва и приравнивают его к нулю: R R R2 R3 ; Z( p) R p L 0 p Rэкв 10 142 1 экв 1 R R экв L 0,007 c 2 3 Постоянная времени цепи: 1 p 1 142 7,04 103с 7,02 мс. Теоретически переходный процесс продолжается бесконечно долго. На практике длительность переходного процесса, с погрешностью до 5% равна 3τ, а с погрешностью до 1% равна 4,6τ, за это время свободная составляющая переходной функции уменьшается в 100 раз. tПП 4,6 4,6 0, 25 103с 1,15 мс. в) Общее решение однородного дифференциального уравнения цепи: i (t) A ept A e RЭквt L ; i(t) i (t) i (t) E0 A ept. Lсв L Lпр Lсв RЭкв Чтобы получить частное решение ОДУ (конечный результат) надо найти постоянные интегрирования в выражении общего решения. Найдём постоянную интегрирования A, которая входит в выражение для iLсв(t). Определение постоянных интегрирования. Постоянныеинтегрированиянаходят, используя независимые и зависимые начальные условия, найденные в первых двух пунктах решения, и законы коммутации, в этой задаче закон коммутации: iL(0+) = iL(0–). Искомая переходная функция времени iL(t): i(t) i (t) i (t) E0 A ept. L Lпр Lсв RЭкв i(0) E0 A 0,3А, A i(0) i (0) i(0) E0 0,3А . L RL Lпр L R Экв Экв iL(t) iLпр(t) iLсв(t) 0,3 e142tА. Получив какую-либо одну переходную функцию времени, можно найти переходные функции остальных токов и напряжений в цепи: uR1 (t) iL (t) R1 3 e142tВ; u(t) L diLL dt 0,02 (0 142 0,5 e142t) 1,42 e142tВ; Рассчитал напряжение uR(t) на основе известных параметров цепи согласно заданному варианту (таблица 2.1). Расчётную и экспериментальную зависимости uR(t) привел на одном графике(Рисунок 6): 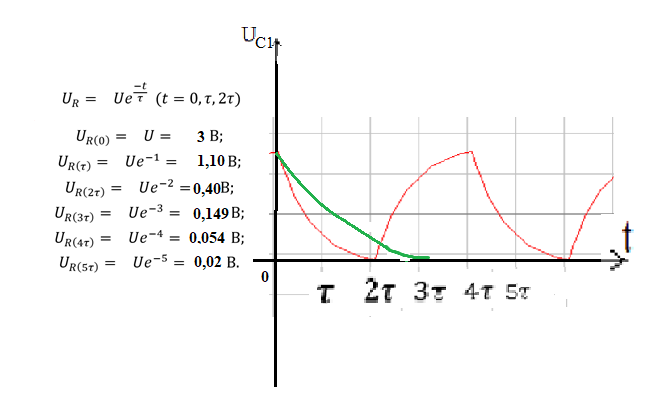 Рисунок 6- Расчётная и экспериментальная зависимости uС(t) Вывод: получил навыки экспериментального исследования переходных процессов в цепи с одним накопителем энергии. Список литературы Основная: Бессонов Л. А. Теоретические основы электротехники. – М.: Гардарики, 2013. – 638 с. Прянишников В. А. ТОЭ: Курс лекций: Учебное пособие – 3-е изд., перераб. и доп. – СПб., 2012 – 368 с. Атабеков Г. И. ТОЭ. Линейные электрические цепи. – СПб.: «Лань», 2010. Аршидинов М. М., Денисенко В. И., Болдырева Л. П. Теоретические основы электротехники: Учебное пособие, АУЭС, Алматы, 2016. – 98 с. Дополнительная: Шебес М. Р., Каблукова М. В. Задачник по теории линейных электрических цепей. – М.: Высшая школа, 1990. – 544 с. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench. В 2-х томах/ Под ред. Д. И. Панфилова – М.: ДОДЭКА, 1999. – т.1 – Электротехника. – 304 с. |
