УЧЕБНОЕ ИССЛЕДОВАНИЕ ПО ЭЛЕМЕНТАМ ВЫСШЕЙ МАТЕМАТИКИ ПРИ ОБУЧЕНИИ ПО ПРОГРАММАМ СПО. Статья-3. Исследование по элементам высшей математики при обучении по программам спо
 Скачать 252.51 Kb. Скачать 252.51 Kb.
|
|
УЧЕБНОЕ ИССЛЕДОВАНИЕ ПО ЭЛЕМЕНТАМ ВЫСШЕЙ МАТЕМАТИКИ ПРИ ОБУЧЕНИИ ПО ПРОГРАММАМ СПО Игонин Захар Дмитриевич студент, ФГБОУ ВО «Елецкий государственный университет им. И. А. Бунина» г. Елец, Российская Федерация Положения элементов высшей математики мы, как обучающиеся зачастую принимаем без сомнений в авторитете автора учебника, лектора, больших данных интернета. Но самостоятельное исследование выдвинутого положения оставляет теорию в долговременной памяти, позволяет быстрее и менее затратно, своевременно актуализировать необходимую для решения задачи теорию. Среди изобилия вопросов интегрального исчисления, опирающихся на строгую теоретическую базу – таблица первообразных, методы интегрирования и др. на финальном этапе изучения рассматривается возможность вычисления интеграла приближённо. Всё, что связано с упомянутыми способами, процессуально походит на исследовательский процесс. В качестве самостоятельного задания нам было предложено разбиться на малые группы, исследовать проблему и представить выводы с использованием цифровых инструментов. Тема исследовательского проекта: «Сравнительная точность приближённых методов нахождения определённого интеграла по формуле прямоугольников, трапеций и параболических трапеций при одинаковом количестве точек деления промежутка интегрирования». Цель исследования: подтвердить наибольшую точность метода параболических трапеций приближённого вычисления определённых интегралов по сравнению с формулами прямоугольников и трапеций. Ход исследования: Нахождение значения определённого интеграла с помощью вычислительного устройства. Выбор количества точек деления промежутка интегрирования и подсчёт значения интеграла по формуле прямоугольников. Подсчёт значения определённого интеграла по формуле трапеций. Выполнение подсчёта по формуле параболических трапеций. Сравнение результатов. Выводы. Представление подсчётов и результатов на интерактивной доске Padlet и предъявление группе. Задача: найти значение интеграла 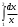 (количество точек деления n=10). (количество точек деления n=10).Используем калькулятор смартфона для решения задачи, предварительно применив формулу Ньютона-Лейбница: 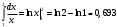 Используем для подсчёта формулу прямоугольников, где 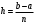 . .В соответствии с выбранным количеством точек деления, таковыми будут 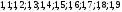 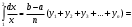 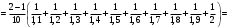 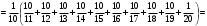 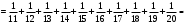 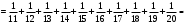 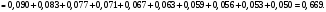 Используем для подсчёта формулу трапеций c теми же точками деления: 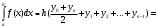 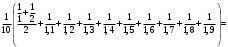 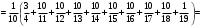 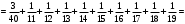 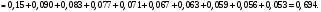 . .Используем для подсчёта формулу параболических трапеций c теми же точками деления (кстати, для текущей формулы количество точек деления должно быть чётным): 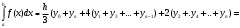 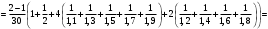 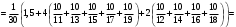 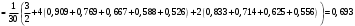 Согласно замечания, при одном и том же количестве точек деления применённые прибижённые формулы в сравнительном рассмотрении имеют иерархию точности. Самая точная – третья формула, вторая точнее первой. Именно это положение и подтверждают использованные формулы приближённого вычисления определённых интегралов. Они достаточно трудоёмки в подсчётах, но выигрывают в случаях, когда требуется показать возможность осуществления аналитической операции интегрирования при отсутствии систематических знаний, без их использования. Полученные результаты представляются на интерактивной доске для совместной работы: 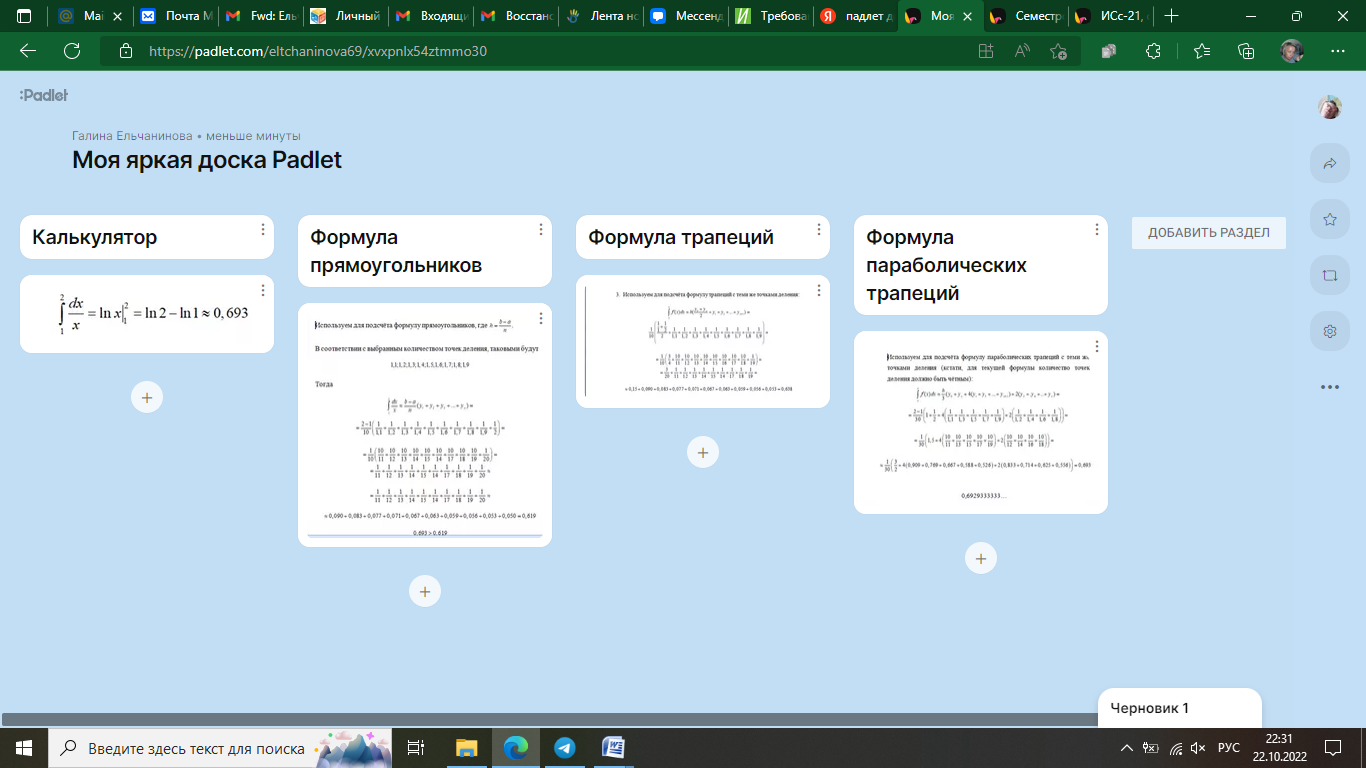 Кроме того, исследования по материалу дисциплины Элементы высшей математики – прерогатива послевузовского образования. Мы, как студенты СПО, имеем небольшой выбор. И приближённые методы вычисления определённых интегралов – одна из немногих тем, по которым мы можем провеcти, пусть и учебное, исследование. Запорожец, Г.И. Руководство к решению задач по математическому анализу: учебное пособие. Г. И. Запорожец. Изд. 8-е, стер. – Санкт-Петербург, Лань, 2014. – 459 с. |
