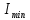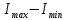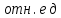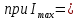Закон малюса. 4.03 Закон Малюса. Исследование поляризованного света. Закон малюса учебнометодическое пособие
 Скачать 0.53 Mb. Скачать 0.53 Mb.
|
Министерство образования и науки Российской Федерации Дальневосточный федеральный университет Школа естественных наук ИССЛЕДОВАНИЕ ПОЛЯРИЗОВАННОГО СВЕТА. ЗАКОН МАЛЮСА Учебно-методическое пособие к лабораторной работе № 4.03 по дисциплине «Физический практикум» Владивосток Дальневосточный федеральный университет УДК53(о76.5) ББК 22.343 Э-41 Составители: О.М. Устинова, Н.Н. Ставнистый, Е.А. Коблова
© ФГАОУ ВПО «ДВФУ», 2014 Цели данной работы: а) экспериментальная проверка закона Малюса; б) определение степени поляризации излучения лазера. Краткая теория Электромагнитные волны – это распространяющееся в пространстве переменное электромагнитное поле. В каждой своей точке такое поле характеризуется вектором напряженности электрического 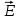 поля и вектором индукции магнитного поля и вектором индукции магнитного 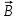 поля, которые изменяются со временем, но направлены всегда перпендикулярно друг другу. Электромагнитные волны поперечны: векторы поля, которые изменяются со временем, но направлены всегда перпендикулярно друг другу. Электромагнитные волны поперечны: векторы 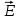 и и 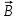 поля волны лежат в плоскости, перпендикулярной к направлению распространения волны, т.е. к вектору скорости поля волны лежат в плоскости, перпендикулярной к направлению распространения волны, т.е. к вектору скорости 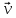 в рассматриваемой точке поля, причем векторы в рассматриваемой точке поля, причем векторы 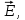 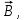 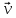 образуют правовинтовую систему. Кроме того, в электромагнитной волне образуют правовинтовую систему. Кроме того, в электромагнитной волне 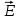 и и 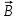 всегда колеблются в одинаковых фазах (синфазно). Это означает, что векторы всегда колеблются в одинаковых фазах (синфазно). Это означает, что векторы 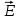 и и 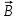 одновременно достигают в одних и тех же точках своего максимального или минимального значения. Электромагнитную волну графически можно представить в виде двух синусоид, расположенных во взаимно перпендикулярных плоскостях (рис.1). Одна из синусоид отражает колебания электрического вектора одновременно достигают в одних и тех же точках своего максимального или минимального значения. Электромагнитную волну графически можно представить в виде двух синусоид, расположенных во взаимно перпендикулярных плоскостях (рис.1). Одна из синусоид отражает колебания электрического вектора 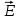 , а другая - магнитного вектора , а другая - магнитного вектора 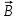 . .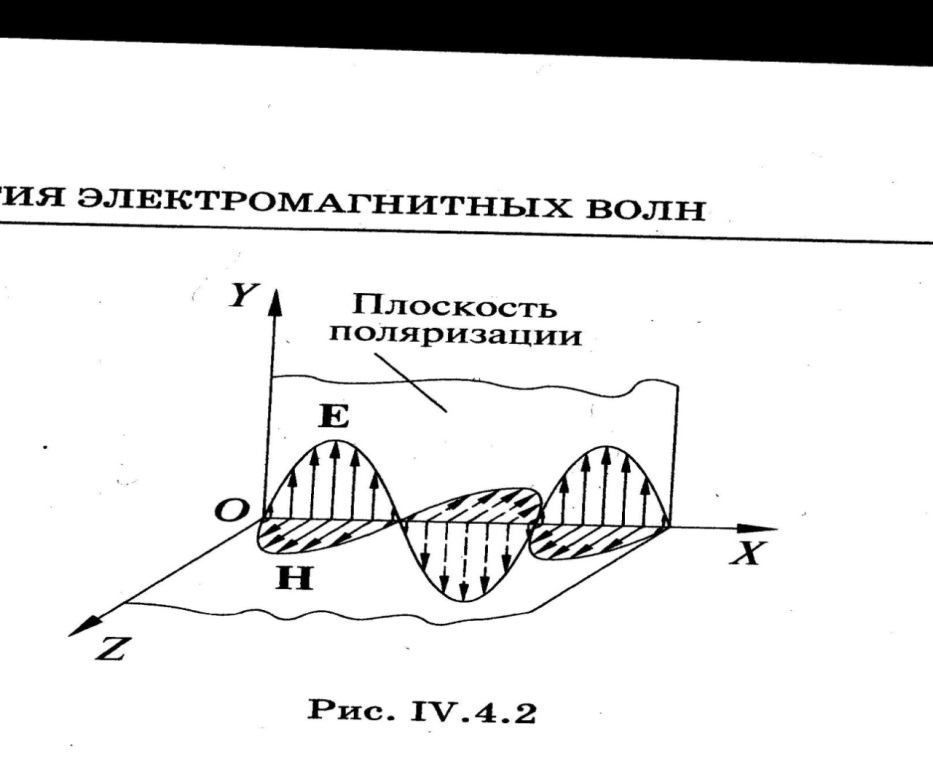 Рис. 1 Различают несколько видов электромагнитных волн: радиоволны, световые волны, рентгеновское и γ-излучение. В зависимости от области действия световые волны подразделяют на:
В дальнейшем нас будет интересовать излучение ВО – так называемый свет. Опыт показывает, что все действия света (фотоэлектрическое, фотохимическое, физиологическое и др.) связаны с вектора 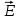 , поэтому принято говорить о световом векторе, имея в виду , поэтому принято говорить о световом векторе, имея в виду 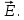 Модуль амплитуды светового вектора будем обозначать буквой А. Изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, описывается уравнением Е=Аsin(ωt–kr+ϕ), где k– волновое число, r - расстояние, отсчитываемое вдоль направления распространения световой волны. Модуль амплитуды светового вектора будем обозначать буквой А. Изменение во времени и пространстве проекции светового вектора на направление, вдоль которого он колеблется, описывается уравнением Е=Аsin(ωt–kr+ϕ), где k– волновое число, r - расстояние, отсчитываемое вдоль направления распространения световой волны. Поляризованный свет, его виды и способы получения Испускаемый каким-либо источником свет, представляет собой суммарное электромагнитное излучение множества атомов. Атомы излучают независимо друг от друга. Процесс излучения отдельного атома продолжается 10-8 с. За это время он переходит из возбужденного в основное состояние, излучая при этом цуг волны - отрезок синусоиды протяженностью примерно 3 м. Излучив, атом через некоторое время, придя в возбужденное состояние, излучает опять и т.д. Одновременно излучают множество атомов. В отдельном цуге колебания вектора 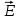 происходят вдоль одного направления в пространстве. Причем для разных цугов волн направления колебаний будут разными. Поэтому в результирующей световой волне колебания светового вектора происходят в разных направлениях с равной вероятностью. Это надо понимать так, что при прохождении света через некоторую точку колебания светового вектора быстро и беспорядочно сменяют друг друга. Такой свет называется естественным или неполяризованным. В естественном свете амплитуда колебаний вектора происходят вдоль одного направления в пространстве. Причем для разных цугов волн направления колебаний будут разными. Поэтому в результирующей световой волне колебания светового вектора происходят в разных направлениях с равной вероятностью. Это надо понимать так, что при прохождении света через некоторую точку колебания светового вектора быстро и беспорядочно сменяют друг друга. Такой свет называется естественным или неполяризованным. В естественном свете амплитуда колебаний вектора 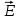 во всех направлениях одинакова. Условно это изображено на рис. 2а, где направление распространения волны перпендикулярно плоскости рисунка. во всех направлениях одинакова. Условно это изображено на рис. 2а, где направление распространения волны перпендикулярно плоскости рисунка. Световая волна, у которой направление колебаний вектора 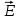 упорядочены каким-либо образом, называется поляризованной. Если колебания вектора упорядочены каким-либо образом, называется поляризованной. Если колебания вектора 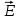 происходят только в одном направлении, перпендикулярном лучу (рис.2 б), то свет называется плоскополяризованным (линейно поляризованным). Плоскость, проходящая через направление колебаний электрического вектора происходят только в одном направлении, перпендикулярном лучу (рис.2 б), то свет называется плоскополяризованным (линейно поляризованным). Плоскость, проходящая через направление колебаний электрического вектора 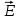 плоско поляризованной волны и направлением распространения этой волны, называется плоскостью поляризации. Свет, в котором представлены колебания вектора плоско поляризованной волны и направлением распространения этой волны, называется плоскостью поляризации. Свет, в котором представлены колебания вектора 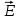 всех направлений, но имеется какое-то преимущественное направление (рис.2в), называется частично поляризованным. Если свет представляет собой такую волну, в которой электрический вектор всех направлений, но имеется какое-то преимущественное направление (рис.2в), называется частично поляризованным. Если свет представляет собой такую волну, в которой электрический вектор 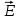 вращается со временем так, что конец его описывает эллипс, то такой свет называется эллиптически поляризованным. Если конец вектора вращается со временем так, что конец его описывает эллипс, то такой свет называется эллиптически поляризованным. Если конец вектора 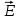 описывает окружность, свет называют поляризованным по кругу. описывает окружность, свет называют поляризованным по кругу. а) б) в) 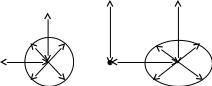 Рис. 2 Поляризацией света называется выделение ППС из естественного или частично поляризованного света. Для этой цели используются специальные устройства, называемые поляризаторами. Принцип действия поляризаторов может быть основан на явлениях отражения, преломления или поглощения света. Например, у некоторых кристаллов коэффициенты поглощения для двух взаимно перпендикулярно поляризованных волн отличаются настолько сильно, что даже при небольшой толщине кристалла одна из волн практически полностью поглощается. В результате из кристалла выходит плоско поляризованный свет. Зависимость величины поглощения света от его поляризации носит название дихроизма, а соответствующие материалы называются дихроическими. Дихроические пластинки используются для изготовления поляризаторов специального вида - поляроидов. Поляризатор может быть использован для анализа поляризованного света, т.е. в качестве анализатора. Главной плоскостью (плоскостью пропускания) поляризатора называется плоскость поляризации света, пропускаемого поляризатором (анализатором). Закон Малюса Пусть на поляризатор падает естественный свет, интенсивность которого Iест. Колебания 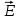 , имеющие амплитуду А, совершающиеся в плоскости, образующей угол 𝛗 с главной плоскостью (ГП) поляризатора, можно разложить на два колебания с амплитудами Апар=Асоs𝛗 и Апер=Аsin𝛗 (на рис. 3 луч перпендикулярен плоскости рисунка). , имеющие амплитуду А, совершающиеся в плоскости, образующей угол 𝛗 с главной плоскостью (ГП) поляризатора, можно разложить на два колебания с амплитудами Апар=Асоs𝛗 и Апер=Аsin𝛗 (на рис. 3 луч перпендикулярен плоскости рисунка).  Рис. 3 Первое колебание пройдет через прибор, второе будет задержано. Интенсивность прошедшей волны пропорциональна А2пар=А2соs 2 𝛗 , т.е. равна Iест ·соs2 𝛗. В естественном свете все значения 𝛗 равновероятны. Поэтому интенсивность света, прошедшего через поляризатор, будет пропорциональна среднему значению соs2 𝛗: 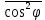 = =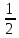 . Следовательно, интенсивность прошедшего поляризованного света не зависит от ориентации поляризатора (т.е. поворота вокруг луча) и равна половине интенсивности падающего естественного света: . Следовательно, интенсивность прошедшего поляризованного света не зависит от ориентации поляризатора (т.е. поворота вокруг луча) и равна половине интенсивности падающего естественного света:I= 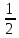 Iест (1) Iест (1)Пусть на анализатор падает плоско поляризованный свет амплитуды А0 и интенсивности I0. Сквозь прибор пройдет составляющая колебания с амплитудой А=А0·соs 𝛗, где 𝛗 – угол между плоскостью колебаний светового вектора 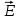 падающего света и главной плоскостью поляризатора. Следовательно, интенсивность прошедшего света определяется выражением падающего света и главной плоскостью поляризатора. Следовательно, интенсивность прошедшего света определяется выражениемI=I0 ·соs2 𝛗 (2) Соотношение (2) носит название закона Малюса. Поставим на пути естественного луча поляризатор и анализатор, главные плоскости которых образуют угол 𝛗. Из первого поляризатора выйдет плоско поляризованный свет, интенсивность которого I0 составляет половину интенсивности естественного света, т.е. 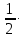 Iест.. Согласно закону Малюса, из анализатора выйдет свет интенсивности I0·соs2𝛗 . Таким образом, интенсивность света, прошедшего через поляризатор и анализатор (два поляризатора), равна Iест.. Согласно закону Малюса, из анализатора выйдет свет интенсивности I0·соs2𝛗 . Таким образом, интенсивность света, прошедшего через поляризатор и анализатор (два поляризатора), равнаI= 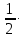 Iест ·соs2 𝛗 Iест ·соs2 𝛗 Максимальная интенсивность равна 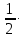 Iест, получается при 𝛗=0 (главные плоскости поляризаторов параллельны). При 𝛗 = π/2 интенсивность равна нулю – «скрещенные» поляризаторы свет не пропускают. Iест, получается при 𝛗=0 (главные плоскости поляризаторов параллельны). При 𝛗 = π/2 интенсивность равна нулю – «скрещенные» поляризаторы свет не пропускают.В некоторых случаях, поляризатор задерживает колебания, перпендикулярные к его главной плоскости, только частично. Такой поляризатор называют несовершенным. На выходе из несовершенного поляризатора получается свет, в котором колебания одного направления преобладают над колебаниями другого направления – это так называемый частично поляризованный свет. Его можно рассматривать как смесь естественного и плоско поляризованного света. Если пропустить частично поляризованный свет через поляризатор, то при его вращении вокруг направления луча интенсивность прошедшего света будет изменяться в пределах от Imax до Imin. Переход одного из этих значений к другому будет совершаться при повороте на угол 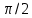 . Выражение . Выражение Р= 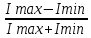 (3) (3)называют степенью поляризации. Для плоско поляризованного света Imin=0 и Р=1, для естественного света Imax = Imin и Р=0. Экспериментальная часть Описание установки Схема установки показана на рис.4. Экспериментальная установка состоит из оптической скамьи (2), гелий-неонового лазера (1) мощностью 1 мВт, поляроида (3) на стержне, фотометрического датчика (4) и цифрового мультиметра (5). Плоско поляризованный световой пучок, излучаемый лазером, падает на анализатор (так называется поляроид, используемый для исследования поляризованного света). Анализатор закреплен в держателе с поворотным устройством с радиально нанесенными делениями. Одно малое деление соответствует повороту поляроида на 10. Вращая анализатор вокруг луча можно добиться положения, когда плоскость колебаний плоско поляризованного света, вышедшего из лазера, и плоскость колебаний поляроида будут или параллельны, или скрещены под углом 900. В первом случае на выходе из анализатора получим максимальный световой поток, который падает на фотоэлемент (4); во втором случае – свет через анализатор не проходит. Интенсивность I света, прошедшего через анализатор и падающего на фотоэлемент, в соответствии с законом фотоэффекта Столетова, пропорциональна силе тока насыщения 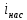 фотоэлемента, т.е. I фотоэлемента, т.е. I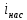 . С другой стороны, фототок насыщения . С другой стороны, фототок насыщения 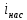 прямо пропорционален напряжению сигнала U (т.е. прямо пропорционален напряжению сигнала U (т.е. 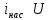 ), который регистрируется цифровым мультиметром. Таким образом, в лабораторной работе об интенсивности света можно судить по величине снимаемого мультиметром напряжения (интенсивность света при этом измеряется в относительных единицах). ), который регистрируется цифровым мультиметром. Таким образом, в лабораторной работе об интенсивности света можно судить по величине снимаемого мультиметром напряжения (интенсивность света при этом измеряется в относительных единицах). Рис.4 Проведение эксперимента Задание 1. Определение степени поляризации лазерного излучения и проверка закона Малюса Включите лазер и, регулируя положение анализатора и фотодатчика, добейтесь попадания лазерного луча на фотодатчик. Включите мультиметр и, вращая анализатор, убедитесь, что мультиметр реагирует на эти вращения. Перекройте лазерный луч плотным листом бумаги и определите фоновое значение интенсивности 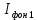 , создаваемое посторонними источниками света. Результат запишите в табл.1 , создаваемое посторонними источниками света. Результат запишите в табл.1Вращая поляроид, найдите такое его положение, при котором сигнал, регистрируемый мультиметром, полностью непроходим к фотодатчику. В соответствии с законом Малюса (2) этому  соответствует значение угла 𝛗, равное 900. соответствует значение угла 𝛗, равное 900.Табл. 1
Вращая поляроид, найдите такое его положение, при котором сигнал, регистрируемый мультиметром, будет максимален. Результат  запишите в табл.1. В соответствии с законом Малюса (2) этому значению запишите в табл.1. В соответствии с законом Малюса (2) этому значению 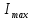 соответствует значение угла соответствует значение угла 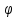 , равное 00. , равное 00.Снимите зависимость интенсивности света, прошедшего через поляроид, от угла поворота 𝛼 поляроида в интервале от -900 до +900 с шагом 50. Результаты запишите в табл.2. После окончания измерений, определите фоновое значение интенсивности. Результат запишите в табл.1 Табл. 2
Обработка результатов эксперимента Если фоновое значение интенсивности 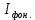 существенно (табл.1), то его нужно учесть в дальнейших расчетах. существенно (табл.1), то его нужно учесть в дальнейших расчетах.Рассчитать среднее фоновое значение интенсивности по формуле: 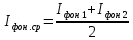 (9) (9)Результат записать в табл.1. По данным табл.2 постройте график зависимости интенсивности света 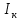 ,, прошедшего через поляроид, от значения угла ,, прошедшего через поляроид, от значения угла 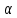 . Угол α – положение поляроида по угловой шкале. Максимальному значению интенсивности . Угол α – положение поляроида по угловой шкале. Максимальному значению интенсивности 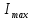 соответствует α0 (значение α0 это и есть действительный ноль шкалы анализатора в данной работе). Найти α0 и записать в табл.2 . соответствует α0 (значение α0 это и есть действительный ноль шкалы анализатора в данной работе). Найти α0 и записать в табл.2 .Вычислите для каждого значения α соответствующий ему угол 𝛗 по формуле: 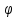 к= αк- α0., где к= αк- α0., где 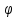 – это угол между плоскостью поляризации световой волны и плоскостью пропускания анализатора. – это угол между плоскостью поляризации световой волны и плоскостью пропускания анализатора.Постройте в полярных координатах график экспериментальной зависимости 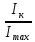 =f1( =f1(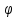 ) )На том же листе постройте по данным табл.3 теоретическую зависимость f1( 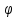 ) = cos2 ) = cos2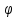 Табл.3
По данным табл.2 и табл.3 постройте в декартовых координатах график 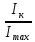 =f(cos 2 =f(cos 2 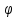 ) )Из всех значений 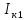 (табл.2) выберите максимальное (табл.2) выберите максимальное 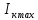 и минимальное и минимальное 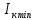 значения интенсивности света, прошедшего через анализатор. Вычислить их разность: значения интенсивности света, прошедшего через анализатор. Вычислить их разность: 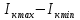 . Результаты записать в табл.1. . Результаты записать в табл.1. По формуле (3) вычислите степень поляризации лазерного излучения. Напишите вывод. Контрольные вопросы В чем заключается свойство поперечности электромагнитных волн? Что такое поляризованный свет? Какие виды поляризации Вы знаете? Что можно сказать о направлениях колебаний светового вектора в случае естественного света и в случае плоско поляризованного света? Что такое частично поляризованный свет? В чем заключается закон Малюса? Как можно получить плоско поляризованный свет? Что такое оптическая ось кристалла? Что такое дихроизм? Пояснить принцип действия поляризационного светофильтра (поляроида). Что такое степень поляризации? Литература: Савельев, И. В. Курс общей физики : учеб. пособие для втузов. В 5 кн. Кн. 3. Оптика / И. В. Савельев. - М. : Астрель : АСТ, 2001. - 336 с. Трофимова, Т. И. Курс физики : рек. М-вом Рос. Федерации в качестве учеб. пособия для инженерно-техн. специальностей высш. учеб.заведений / Т. И. Трофимова. - 13-е изд., стер. - М. : Академия, 2007. - 557 с. - (Высшее профессиональное образование). Учебное издание Составители: Устинова Ольга Михайловна Ставнистый Николай Николаевич Коблова Елена Александровна Учебно-методическое пособие К лабораторной работе №4.12 По дисциплине «Физический практикум» Компьютерная верстка: Устинова О.М. Подписано в печать …………. Формат 60  84/16.Усл.печ.л.0,93. Уч.-изд.л.0,78. 84/16.Усл.печ.л.0,93. Уч.-изд.л.0,78.Тираж 100 экз. Заказ Дальневосточный федеральный университет 690091, г. Владивосток, ул.Суханова, 8 Отпечатано на кафедре общей физики ШЕН ДВФУ 690091, г. Владивосток, ул.Суханова, 8 |

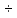 0,40 мкм
0,40 мкм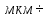 1 мм
1 мм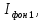
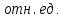
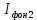 ,
,  .
.