1. Способы определения точек пересечения прямой с плоскостью, с гранной поверхностью

• Название: 1. Способы определения точек пересечения прямой с плоскостью, с гранной поверхностью
• Анкор: Otvety_k_vprosam (1).docx
• Дата: 02.05.2017
• Размер: 3.41 Mb.
• Имя файла: Otvety_k_vprosam (1).docx
• Тип: Документы; #6552

1.Способы определения точек пересечения прямой с плоскостью, с гранной поверхностью.

Если прямая и плоскость не параллельны, то они пересекаются в точке, которая принадлежит как прямой, так и плоскости.

Определение точки пересечения прямой l с плоскостью ABC в общем случае выполняется в такой последовательности:

– через прямую проводят вспомогательную проецирующую плоскость, например, απ₂; ее след α" совпадает с фронтальной проекцией прямой;

– находят линию MN пересечения плоскостей α и ABC;

– фиксируют точку O пересечения прямой l и прямой MN (в данном варианте сначала определяется проекция O' ).

Видимость прямой l по отношению к плоскости ABC определена с помощью пар конкурирующих точек F и G, M и P .
2. Построение линии пересечения плоскости частного и общего положения, двух плоскостей общего положения.

Для построения линии пересечения двух плоскостей a и b необходимо найти две точки, N и M каждая из которых принадлежит обеим плоскостям. Для нахождения точек N и M можно воспользоваться следующим алгоритмом:

21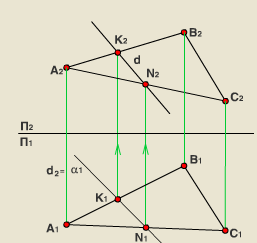




Общ+час: Спроецируем плоскости a и ABC на П1. Плоскость общего положения АВС проецируется на плоскость П1 в виде треугольника А1В1С1, а плоскость частного положения a - в виде прямой a1. На плоскости П1 прямая a1 и АВС пересекаются в точках K1 (K1 принадлежит А1В1) и N1 (N1 принадлежит А1C1). Если через точки K1 и N1 провести проецирующие прямые до пересечения с плоскостью АВС, то получатся две точки K (K принадлежит АВ) и N (N принадлежит АC). Соединив точки K и N, мы получим прямую KN. Прямая KN - линия пересечения плоскости a с плоскостью АВС.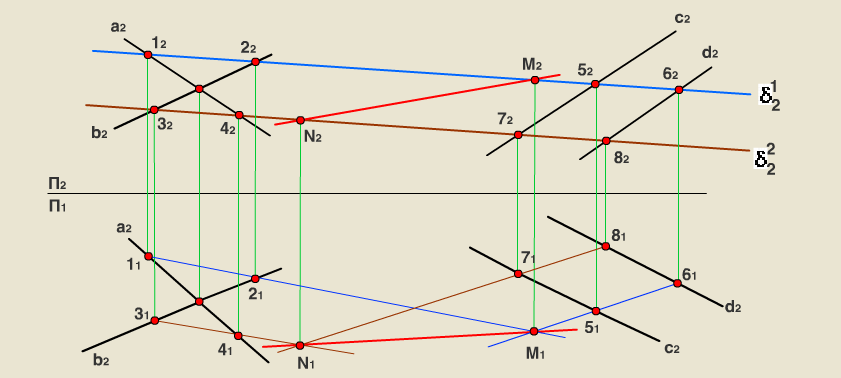




Общего:

1)Взять две дополнительные плоскости частного положения 1ЧП и 2ЧП;

2)Определить линии пересечения плоскостей частного положения 1ЧП и 2ЧП с плоскостями

общего положения a и b с помощью метода, приведенного в предыдущем пункте;

3)Определить точки N и M пересечения полученных линий.


3.Перпендикулярные прямые. Привести пример определения расстояния от точки до прямой общего положения.

Пересекающиеся и скрещивающиеся прямые в пространстве могут располагаться в частности под прямым углом друг к другу. Если обе прямые – общего положения, то факт их перпендикулярности на чертеже не отражается: проекцией прямого угла будет тупой (острый) угол.

И только в случае, если одна из прямых параллельна плоскости проекций, прямой угол проецируется в натуральную величину на ту плоскость, которой прямая параллельна. Это предложение (теорема) является основополагающим для изображения на чертеже взаимно перпендикулярных прямых: тогда и только тогда прямой угол проецируется в натуральную величину, если хотя бы одна его сторона параллельна плоскости проекций, а следовательно, является или фронталью, или горизонталью.

Расстояние от точки до прямой определяется длиной перпендикуляра, опущенного из точки на прямую. Пусть необходимо определить расстояние от точки М до прямой а общего положения.

Через заданную точку M проводится плоскость s перпендикулярная заданной прямой а. Плоскость задается двумя пересекающимися прямыми, фронталью (f) и горизонталью (h): s = h f.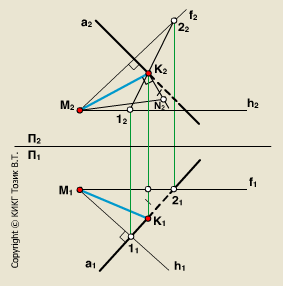
Находится точка пересечения (K) исходной прямой а с плоскостью s.
Определяется расстояние от точки М до точки K способом прямоугольного треугольника. Длина гипотенузы прямоугольного треугольника M2K2N2 равна расстоянию от точки M до прямой а: |MK| = M2N2.
4.Перпендикулярные прямая и плоскость. Привести примеры определения расстояния от точки до плоскости частного положения, от точки до плоскости общего положения. Привести пример построения перпендикуляра заданной длины к плоскости общего положения в точке, принадлежащей плоскости.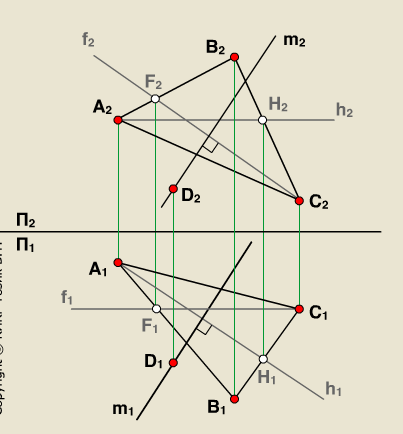
Прямая перпендикулярна плоскости если она перпендикулярна двум пересекающимся прямым этой плоскости.

Для того, чтобы прямая m была перпендикулярна плоскости , необходимо и достаточно, чтобы горизонтальная проекция прямой m₁ была горизонтальной проекции горизонтали (m₁ h₁), а фронтальная проекция прямой m₂ – фронтальной проекции фронтали (m₂ f₂).

Расстояние от точки до плоскости является длина перпендикуляр опущенного из данной точки к данной плоскости.

Длину перпендикуляра можно определить с помощью прямоугольного треугольника.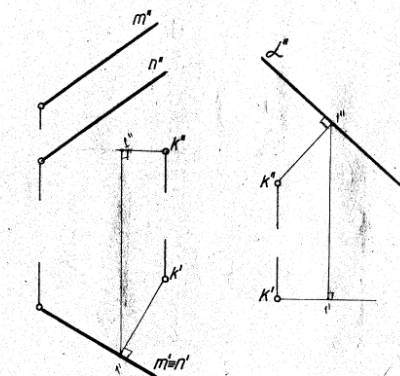

Для построения перпендикуляра заданной длины для начала необходимо построить перпендикуляр произвольной длины, а затем увеличивая гипотенузу можно получить перпендикуляр заданной длины.

5.Перпендикулярные плоскости. Привести пример построения плоскости, перпендикулярной двум заданным плоскостям. Привести пример построения плоскости, параллельной заданной прямой и перпендикулярной заданной плоскости.

Известно, что плоскости перпендикулярны, если одна из них проходит через перпендикуляр к другой.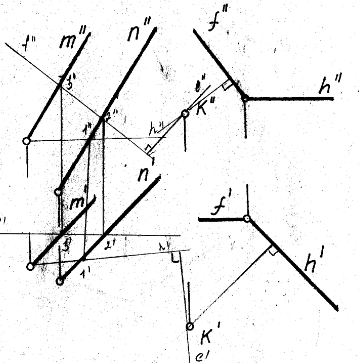

Поэтому, построение плоскости, перпендикулярной данной, предполагает построение перпендикуляра к ней из любой точки, заведомо принадлежащей искомой плоскости.

Известно, что прямая параллельна плоскости, если она параллельна прямой, лежащей в плоскости. Например, прямая m параллельна прямой l, лежащей в плоскости

6. Параллельные прямая и плоскость, параллельные плоскости. Привести примеры.

Прямая параллельна плоскости если она параллельна прямой лежащей в данной плоскости.

Плоскости параллельны если две пересекающиеся прямые одной плоскости параллельны двум пересекающим прямым другой плоскости.
7. Способы определения длины отрезка прямой общего положения. Привести примеры. Определение углов наклона прямой общего положения к плоскостям проекций. Привести примеры.

Длину прямой общего положения можно определить по правилу прямоугольного треугольника.

Где гипотенуза является истиной величиной данного отрезка, один катет равен проекции данной прямой, второй катет равен разности расстояний сторон до плоскости проекций. Угол наклона данной прямой к плоскости проекции определяется как угол между прямой и её проекцией на данную ось. Этот угол есть в том же треугольнике и является острым углом.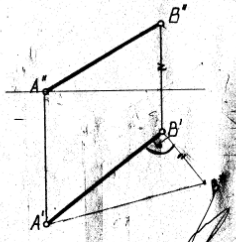

8. Определение расстояний между параллельными прямыми, скрещивающимися прямыми. Привести примеры

Кратчайшим расстояние между параллельными и скрещивающимися прямыми есть перпендикуляр.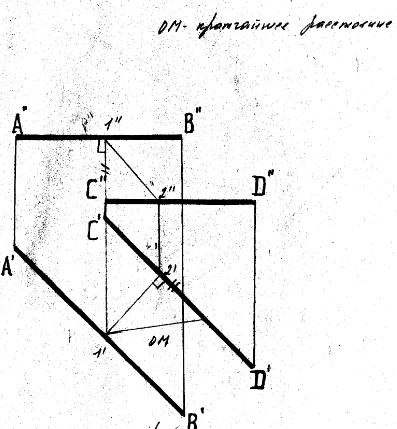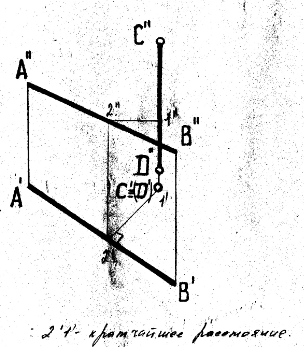


9.Преобразование комплексного чертежа вращением вокруг проецирующей прямой. Привести примеры использования вращения в решении задач.

При вращении вокруг некоторой неподвижной оси, каждая точка вращаемой фигуры перемещается в плоскости перпендикулярной оси вращения. Точка перемещается по окружности цент которой находится в точки пересечения оси с плоскостью вращения, а радиус окружности равен расстоянию от точки до оси вращения. Если точка находится на оси вращения то она сохраняет свое положение.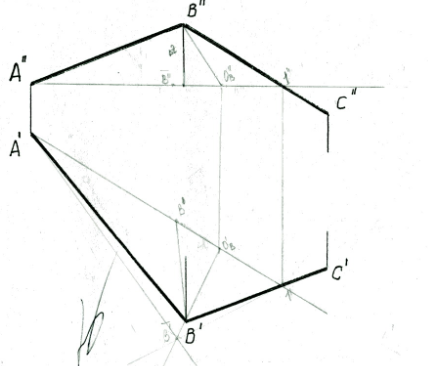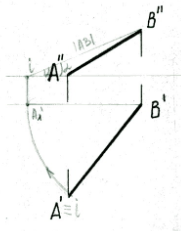



10. Определение величины плоской фигуры вращением вокруг ее линии уровня. Привести примеры.

Для того чтобы получить истинную величину плоской фигуры необходимо чтобы она заняла положение параллельное плоскости проекции. Для этого можно повернуть её вокруг лини уровня (к примеру горизонтали) так чтобы она заняла положение параллельное плоскости проекции.



11. Преобразование комплексного чертежа заменой плоскостей проекций. Привести примеры решения задач этим способом (определение величины расстояния между скрещивающимися прямыми, величины двугранного угла и др.)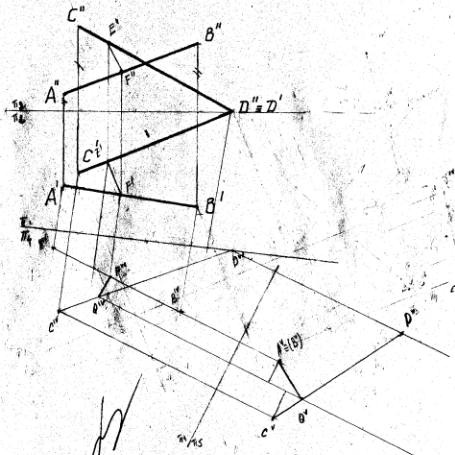

Приведение прямых линий и плоских фигур в частные положения относительно плоскостей проекций в ходе решения задач нередко приводит к значительному упрощению решения.

Способ замены плоскостей проекций заключается в том, что одна из основных плоскостей проекций (π₁ , π₂) заменяется дополнительной плоскостью проекций, подходящим образом расположенной относительно оригинала, но перпендикулярно остающейся плоскости проекций.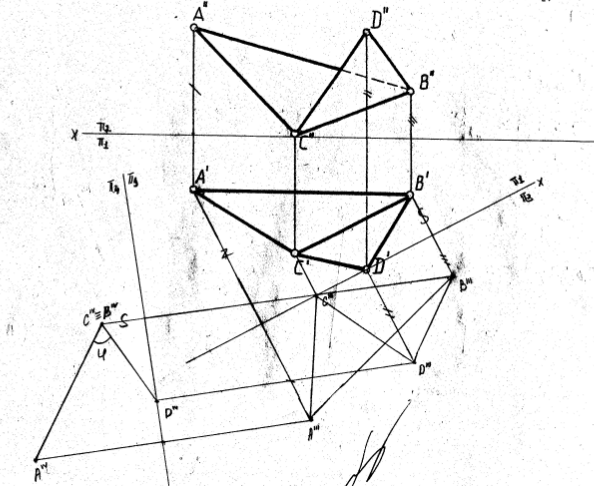






12.Геометрическое место точек, равноудаленных от концов отрезка. Привести примеры определения точки на прямой частного (общего) положения, равноудаленной от концов заданного отрезка.

Геометрическое место точек - это множество всех точек, удовлетворяющих определённым заданным условиям.

Пример 1. Срединный перпендикуляр любого отрезка есть геометрическое место точек (т.е. множество всех точек), равноудалённых от концов этого отрезка.

Пример 2. Окружность - это геометрическое место точек (т.е. множество всех точек), равноудалённых от её центра (одна из этих точек - А).
13. Сечение кривой поверхности плоскостью. Конические сечения. Привести примеры пересечения конической поверхности по эллипсу, параболе, гиперболе, двум образующим. Определение величины сечения.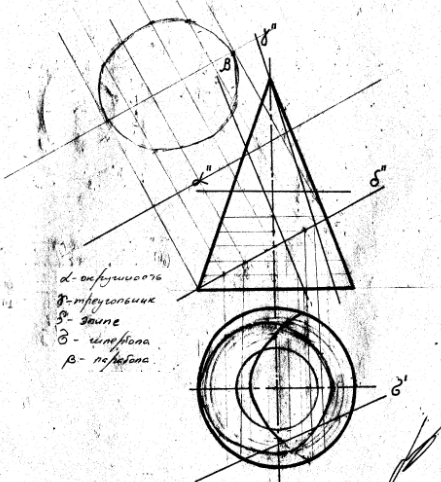

Для нахождения кривой линии, при пересечении линейчатой кривой поверхности с плоскостью, следует в общем случаи строить точки пересечения образующих поверхности с секущей плоскостью.

Если же кривая поверхность не линейчата то, для постарения линии пересечения такой поверхности плоскостью в общем случаи следует применять вспомогательные плоскости. Точки искомой линии определяются точками пересечения по которым вспомогательная секущая плоскость пересекает данные поверхности и секущую плоскость.

Для построения кривой линии получаемой при сечении конической поверхности плоскостью в общем случаи следует искать точки пересечения плоскости с образующими.

Конические сечения есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых. Окружность можно рассматривать как частный случай эллипса.

14.Пересечение с плоскостью поверхности цилиндра, сферы. Привести примеры определения точек пересечения прямой с этими поверхностями.

Для построения кривой линии, получаемой при пересечении цилиндрической поверхности секущей плоскостью, в общем случае следует искать точки пересечения образующих и секущей плоскости. Любая цилиндрическая поверхность пересекается плоскостью, расположенной параллельно образующим этой поверхности по прямым линиям.

Как бы ни была направлена секущая плоскость она всегда рассекает сферу по окружности, которая проецируется в виде отрезка, эллипса, окружности в зависимости от положения секущей плоскости к плоскости проекции.





15.Образование тора, его разновидности. Круговые сечения тора. Привести примеры построения точек пересечения прямой с поверхностью тора.

Тор образуется вращением окружности вокруг неподвижной оси, лежащей в плоскости данной окружности, но не проходящей через центр данной окружности.

Различают :

1)Открытый тор или круговой тор;

2) Замкнутый;

3)Самопересекающий.

Тор имеет две системы круговых сечений : в плоскостях, перпендикулярных к оси вращения и в плоскостях, проходящих через ось вращения.