|
Цилиндр конспект урока. Конспект лекций Цилиндр, конус,шар. и окружность L
Понятие цилиндра. |
Рассмотрим произвольную плоскость α и окружность L с центром О радиуса г, лежащую в этой плоскости. Через каждую точку окружности L проведем прямую, перпендикулярную к плоскости α. Поверхность, образованная этими прямыми, называется цилиндрической поверхностью, а сами прямые — образующими цилиндрической поверхности. Прямая, проходящая через точку О перпендикулярно к плоскости α, называется осью цилиндрической поверхности. Поскольку все образующие и ось перпендикулярны к плоскости α, то они параллельны друг другу (см. п. 16).
Рассмотрим теперь плоскость β, параллельную плоскости α (рис. 142). Отрезки образующих, заключенные между плоскостями α и β, параллельны и равны друг другу (см. п. 11). По построению концы этих отрезков, расположенные в плоскости α, заполняют окружность L. Концы же, расположенные в плоскости β, заполняют окружность L1 с центром О1 радиуса г, где O1 — точка пересечения плоскости β с осью цилиндрической поверхности.
Справедливость этого утверждения следует из того, что множество концов образующих, лежащих в плоскости β, получается из окружности L параллельным переносом на вектор 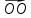 1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор 1. Параллельный перенос является движением и, значит, наложением, а при наложении любая фигура переходит в равную ей фигуру. Следовательно, при параллельном переносе на вектор 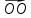 1 окружность L перейдет в равную ей окружность L1 радиуса г с центром в точке О1 1 окружность L перейдет в равную ей окружность L1 радиуса г с центром в точке О1
Тело, ограниченное цилиндрической поверхностью и двумя кругами с границами L и L1называется цилиндром (см. рис. 142). Круги называются основаниями цилиндра, отрезки образующих, заключенные между основаниями, — образующими цилиндра, а образованная ими часть цилиндрической поверхности — боковой поверхностью цилиндра. Ось цилиндрической поверхности называется осью цилиндра.
Как уже отмечалось, все образующие цилиндра параллельны и равны друг другу. Длина образующей называется высотой цилиндра, а радиус основания — радиусом цилиндра.
 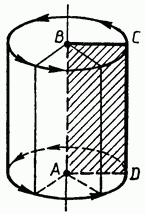 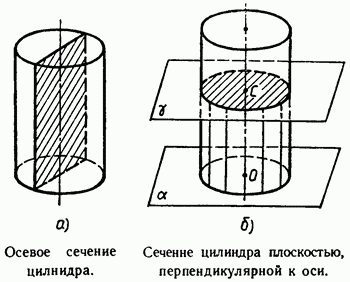
Рис. 42. Рис. 43. Рис. 44. Рис. 45.
Цилиндр может быть получен вращением прямоугольника вокруг одной из его сторон.
На рис.143 изображен цилиндр, полученный вращением прямоугольника ABCD вокруг стороны АВ. При этом боковая поверхность цилиндра образуется вращением стороны CD, а основания — вращением сторон ВС и AD.
Рассмотрим сечения цилиндра различными плоскостями. Если секущая плоскость проходит через ось цилиндра, то сечение представляет собой прямоугольник (рис. 144), две стороны которого — образующие, а две другие — диаметры оснований цилиндра. Такое сечение называется осевым.
Если секущая плоскость перпендикулярна к оси цилиндра, то сечение является кругом. В самом деле, такая секущая плоскость (плоскость γ на рисунке 145) отсекает от данного цилиндра тело, также являющееся цилиндром. Его основаниями служат два круга, один из которых и есть рассматриваемое сечение.
На практике нередко встречаются предметы, которые имеют форму более сложных цилиндров. Мы будем рассматривать только - прямые круговые цилиндры.
|
Площадь поверхности цилиндра
|
На рисунке 147, а изображен цилиндр. Представим себе, что его боковую поверхность разрезали по образующей АВ и развернули таким образом, что все образующие оказались расположенными в некоторой плоскости α (рис. 147, б). В результате в плоскости α получится прямоугольник ABB'A'. Стороны АВ и А'В' прямоугольника представляют собой два края разреза боковой поверхности цилиндра по образующей АВ. Этот прямоугольник называется разверткой боковой поверхности цилиндра. Основание А A'. прямоугольника является разверткой окружности основания цилиндра, а высота АВ — образующей цилиндра, поэтому АА' = 2πг,
АВ = h, где г — радиус цилиндра, h — его высота.
За площадь боковой поверхности цилиндра принимается площадь ее развертки.
Так как площадь прямоугольника ABB'A' равна АА' • АВ = 2πгh, то для вычисления площади Sбок боковой поверхности цилиндра радиуса г и высоты h получается формула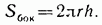 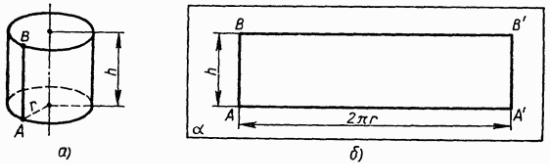 Рис.147 Итак, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра. Рис.147 Итак, площадь боковой поверхности цилиндра равна произведению длины окружности основания на высоту цилиндра.
Площадью полной поверхности цилиндра называется сумма площадей боковой поверхности и двух оснований. Так как площадь каждого основания равна πг2, то для вычисления площади Sцил полной поверхности цилиндра получаем формулу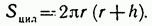
|
Решение задач по теме « Цилиндр»
|
521. Докажите, что осевое сечение цилиндра является прямоугольником, две противоположные стороны которого — образующие, а две другие — диаметры оснований цилиндра. Найдите диагональ осевого сечения, если радиус цилиндра равен 1,5 м, а высота 4м.
|
522. Диагональ осевого сечения цилиндра равна 48 см. Угол между этой диагональю и образующей цилиндра равен 60°. Найдите: а) высоту цилиндра; б) радиус цилиндра; в) площадь основания цилиндра
|
523. Осевое сечение цилиндра — квадрат, диагональ которого равна 20 см. Найдите: а) высоту цилиндра; б) площадь основания цилиндра.
|
524. Осевые сечения двух цилиндров равны. Равны ли высоты этих цилиндров?
|
525. Площадь осевого сечения цилиндра равна 10 см2 а площадь основания —5 см2 Найдите высоту цилиндра.
|
531. Высота цилиндра равна 10 дм. Площадь сечения цилиндра плоскостью, параллельной оси цилиндра и удаленной на 9 дм от нее, равна 240 дм2 Найдите радиус цилиндра
|
538. Площадь боковой поверхности цилиндра равна 5. Найдите площадь осевого сечения цилиндра.
|
545. Цилиндр получен вращением квадрата со стороной а вокруг одной из его сторон. Найдите площадь: а) осевого сечения цилиндра; б) боковой поверхности цилиндра; в) полной поверхности цилиндра.
|
Понятие конуса.
|
Рассмотрим окружность L с центром О и прямую ОР, перпендикулярную к плоскости α этой окружности. Через точку Р и каждую точку окружности проведем прямую. Поверхность, образованная этими прямыми, называется конической поверхностью (рис. 148), а сами прямые — образующими конической поверхности. Точка Р называется вершиной, а прямая ОР — осью конической поверхности.
Тело, ограниченное конической поверхностью и кругом с границей L, называется конусом (рис. 149). Круг называется основанием конуса, вершина конической поверхности — вершиной конуса, отрезки образующих, заключенные между вершиной и основанием, — образующими конуса, а образованная ими часть конической поверхности — боковой поверхностью конуса. Ось конической поверхности называется осью конуса, а ее отрезок, заключенный между вершиной и основанием, — высотой конуса. Отметим, что все образующие конуса равны друг другу (объясните почему).
Конус может быть получен вращением прямоугольного треугольника вокруг одного из его катетов. На рисунке 150 изображен конус, полученный вращением прямоугольного треугольника ABC вокруг катета АВ. При этом боковая поверхность конуса образуется вращением гипотенузы АС, а основание — вращением катета ВС.
Рассмотрим сечение конуса различными плоскостями. Если секущая плоскость проходит через ось конуса (рис. 151), то сечение представляет собой равнобедренный треугольник, основание которого — диаметр основания конуса, а боковые стороны — образующие конуса. Это сечение называется осевым.
Если секущая плоскость перпендикулярна к оси ОР конуса (рис. 152), то сечение конуса представляет собой круг с центром О1, расположенным на оси РО1 конуса. Радиус r1 этого круга равен РО1/ РО г, где г — радиус основания конуса, что легко усмотреть из подобия прямоугольных треугольников РОМ и РО1М1. Доказательство этого факта приведено в решении задачи 556.
 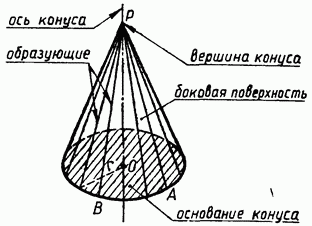 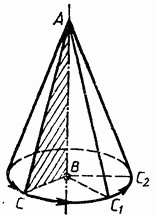  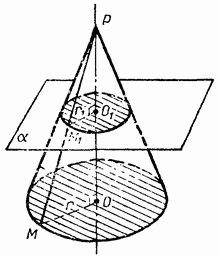
Рис .148 Рис .149 Рис .150 Рис .151 Рис .152
|
Площадь поверхности конуса
|
Боковую поверхность конуса, как и боковую поверхность цилиндра, можно развернуть на плоскость, разрезав ее по одной из образующих (рис. 153, а, б). Разверткой боковой поверхности конуса является круговой сектор (см. рис. 153, б), радиус которого равен образующей конуса, а длина дуги сектора равна длине окружности основания конуса.
За площадь боковой поверхности конуса принимается площадь ее развертки.
Выразим площадь S6oк боковой поверхности конуса через его образующую l и радиус основания г. Площадь кругового сектора — развертки боковой поверхности конуса (см. рис. 153, б) - равна  где α – градусная мера дуги АВА, поэтому где α – градусная мера дуги АВА, поэтому  (1) (1)
|
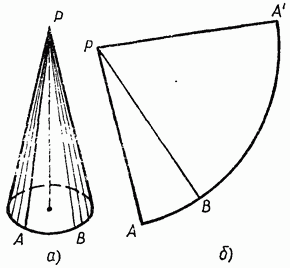
Рис .153
|
Выразим α через l и г. Так как длина дуги АВА' равна 2πг (длине окружности основания конуса),то . Подставив это выражение в формулу (1), получим . Подставив это выражение в формулу (1), получим

Таким образом, площадь боковой поверхности конуса равна произведению половины длины окружности основания на образующую.
Площадью полной поверхности конуса называется сумма площадей боковой поверхности и основания. Для вычисления площади Sконполной поверхности конуса получается формула

|
Усеченный конус
|
Возьмем произвольный конус и проведем секущую плоскость, перпендикулярную к его оси. Эта плоскость пересекается с конусом по кругу и разбивает конус на две части. Одна из частей (верхняя на рис. 154) представляет собой конус, а другая называется усеченным конусом. Основание исходного конуса и круг, полученный в сечении этого конуса плоскостью, называются основаниями усеченного конуса, а отрезок, соединяющий их центры,— высотой усеченного конуса.
Часть конической поверхности, ограничивающая усеченный конус, называется его боковой поверхностью, а отрезки образующих конической поверхности, заключенные между основаниями, называются образующими усеченного конуса. Все образующие усеченного конуса равны друг другу (докажите это самостоятельно).
Усеченный конус может быть получен вращением прямоугольной трапеции вокруг ее боковой стороны, перпендикулярной к основаниям. На рисунке 155 изображен усеченный конус, полученный вращением прямоугольной трапеции ABCD вокруг стороны CD, перпендикулярной к основаниям AD и ВС. При этом боковая поверхность образуется вращением боковой стороны АВ, а основания усеченного конуса — вращением оснований СВ и DA трапеции.
|

Рис .154

Рис .155
|
Можно доказать, что площадь боковой поверхности усеченного конуса равна произведению полусуммы длин окружностей оснований на образующую, т. е. 
где г и г1— радиусы оснований, l — образующая усеченного конуса.
|
547. Высота конуса равна 15 см, а радиус основания равен 8 см. Найдите образующую конуса.
|
548. Образующая конуса, равная 12 см, наклонена к плоскости основания под углом α. Найдите площадь основания конуса, если: а) α = 30°; б) α = 45°; в) α = 60°.
|
550. Осевое сечение конуса — прямоугольный треугольник. Найдите площадь этого сечения, если радиус основания конуса равен 5 см.
|
553. Найдите высоту конуса, если площадь его осевого сечения равна 6 дм2, а площадь основания равна 8 дм2.
|
555. Высота конуса равна 10 см. Найдите площадь сечения, проходящего через вершину конуса и хорду основания, стягивающую дугу в 60°, если плоскость сечения образует с плоскостью основания конуса угол: а) 30°; б) 45°; в) 60°.
|
565.Прямоугольный треугольник с катетами 6 см и 8 см вращается вокруг меньшего катета. Вычислите площади боковой и полной поверхностей образованного при этом вращении конуса.
|
Сфера и шар
|
Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки (рис. 157).
Данная точка называется центром сферы (точка О на рис. 150), а данное расстояние — радиусом сферы. Радиус сферы часто обозначают буквой R.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы, также называется радиусом сферы. Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Очевидно, диаметр сферы равен 2R. Отметим, что сфера может быть получена вращением полуокружности вокруг ее диаметра (рис. 151).
Тело, ограниченное сферой, называется шаром. Центр, радиус и диаметр сферы называются также центром, радиусом и диаметром шара. Очевидно, шар радиуса R с центром О содержит все точки пространства, которые расположены от точки О на расстоянии, не превышающем R (включая и точку О), и не содержит других точек.
|
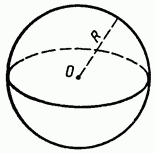
Рис .157
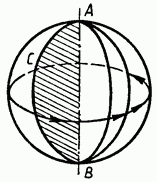
Рис .158
|
Уравнение сферы.
|
Выведем уравнение сферы (см. начало п. 53) радиуса R с центром С (х0; у0; z0) (рис. 159).
Р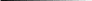 асстояние от произвольной точки М (х; у; z) до точки С вычисляется по формуле MC = асстояние от произвольной точки М (х; у; z) до точки С вычисляется по формуле MC =  (x- x0)2 +(у-у0)2 + (z-z0)2. (x- x0)2 +(у-у0)2 + (z-z0)2.
Если точка М лежит на данной сфере, то МС = R, или МС2 = R2, т. е. координаты точки М удовлетворяют уравнению
(х-х0)2+(у-у0)2+(z-z0)2 =R2. (1)
Если же точка М (х; у; z) не лежит на данной сфере, то МС2 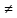 R2, т. е. координаты точки М не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С (x0; у0; z0) имеет вид(х- x0)2 +(у-у0)2 +(z-z0)2 =R2. R2, т. е. координаты точки М не удовлетворяют уравнению (1). Следовательно, в прямоугольной системе координат уравнение сферы радиуса R с центром С (x0; у0; z0) имеет вид(х- x0)2 +(у-у0)2 +(z-z0)2 =R2.
|
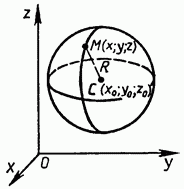
Рис .159
|
Взаимное расположение сферы и плоскости
|
Исследуем взаимное расположение сферы и плоскости в зависимости от соотношения между радиусом сферы и расстоянием от ее центра до плоскости.
Обозначим радиус сферы буквой R, а расстояние от ее центра до плоскости α — буквой d. Введем систему координат так, как показано на рис. 160: плоскость Оху совпадает с плоскостью α, а центр С сферы лежит на положительной полуоси Oz. В этой системе координат точка С имеет координаты (0; 0; d), поэтому сфера имеет уравнение х2+ у2+ (z – d)2 = R2. Плоскость α совпадает с координатной плоскостью Оху, и поэтому ее уравнение имеет вид z = 0 (объясните почему).
Если координаты какой-нибудь точки М (х; у; z) удовлетворяют обоим уравнениям, то точка М лежит как в плоскости а, так и на сфере, т. е. является общей точкой плоскости и сферы.
Если же система этих двух уравнений не имеет решений, то сфера и плоскость не имеют общих точек. Таким образом, вопрос о взаимном расположении сферы и плоскости сводится к исследованию системы уравнений Подставив z = 0 во второе уравнение, получим х2+ у2= R2- d2 (2) Подставив z = 0 во второе уравнение, получим х2+ у2= R2- d2 (2)
Возможны три случая.
|
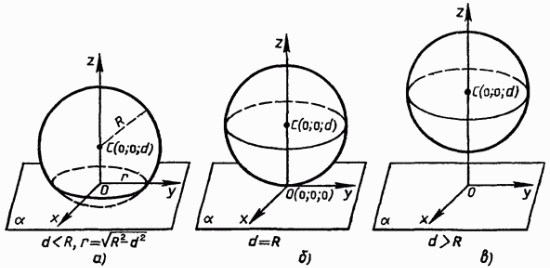   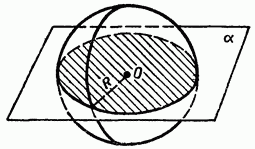 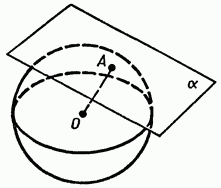
Рис .160 Рис .161 Рис .162
1.d < R. Тогда R2- d2> 0, и уравнение (2) является уравнением окружности радиуса г =  R2- d2 R2- d2
с центром в точке О на плоскости Оху. Координаты любой точки М (х; у; 0) этой окружности удовлетворяют как уравнению плоскости а, так и уравнению сферы, т. е. все точки этой окружности являются общими точками плоскости и сферы (см. рис. 160, а).
Таким образом, в данном случае сфера и плоскость пересекаются по окружности. Итак, если расстояние от центра сферы до плоскости меньше радиуса сферы, то сечение сферы плоскостью есть окружность.
Ясно, что сечение шара плоскостью есть круг. Если секущая плоскость проходит через центр шара, то d = 0 и в сечении получается круг радиуса R, т. е. круг, радиус которого равен радиусу шара. Такой круг называется большим кругом шара (рис. 161).
Если секущая плоскость не проходит через центр шара, то d > 0 и радиус сечения
г =  R2– d 2 , очевидно, меньше радиуса шара (см. рис. 160, а). R2– d 2 , очевидно, меньше радиуса шара (см. рис. 160, а).
2. d = R. Тогда R2- d2= 0, и уравнению (2) удовлетворяют только числа х = 0, у = 0. Следовательно, только координаты точки О (0; 0; 0) удовлетворяют обоим уравнениям, т. е. О — единственная общая точка сферы и плоскости (см. рис. 160, б). Итак, если расстояние от центра сферы до плоскости равно радиусу сферы, то сфера и плоскость имеют только одну общую точку.
3. d> R. Тогда R2- d2< 0, и уравнению (2) не удовлетворяют координаты никакой точки. Следовательно, если расстояние от центра сферы до плоскости больше радиуса сферы, то сфера и плоскость не имеют общих точек (см. рис. 160, в).
|
Касательная плоскость к сфере
|
Рассмотрим более подробно случай, когда сфера и плоскость имеют только одну общую точку.
Плоскость, имеющая со сферой только одну общую точку, называется касательной плоскостью к сфере, а их общая точка называется точкой касания плоскости и сферы.
На рис.162 плоскость α- касательная к сфере с центром О, А - точка касания. Касательная плоскость к сфере обладает свойством, аналогичным свойству касательной к окружности. Оно выражено в следующей теореме:
Радиус сферы, проведенный в точку касания сферы и плоскости, перпендикулярен к касательной плоскости.
Доказательство: Рассмотрим плоскость а, касающуюся сферы с центром О в точке А (рис. 162). Докажем, что радиус ОА перпендикулярен к плоскости α.Предположим, что это не так. Тогда радиус ОА является наклонной к плоскости α, и, следовательно, расстояние от центра сферы до плоскости α меньше радиуса сферы. Поэтому сфера и плоскость пересекаются по окружности. Но это противоречит тому, что плоскость α -касательная, т. е. сфера и плоскость а имеют только одну общую точку. Полученное противоречие доказывает, что радиус ОА перпендикулярен к плоскостиα. Теорема доказана.
Обратная теорема. Если радиус сферы перпендикулярен к плоскости, проходящей через его конец, лежащий на сфере, то эта плоскость является касательной к сфере.(Самостоятельно)
Формула для вычисления площади сферы радиуса R: S = 4πг2
| |
|
|
 Скачать 1.61 Mb.
Скачать 1.61 Mb.