РЛ1-92_Лаба2_отчет. Исследование помехоустойчивости систем радиопередачи информации
 Скачать 306.18 Kb. Скачать 306.18 Kb.
|
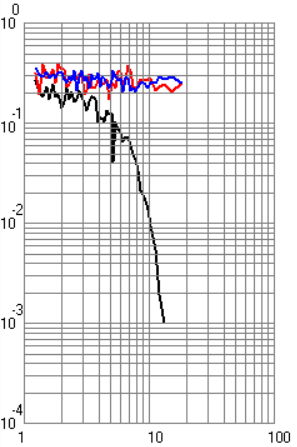
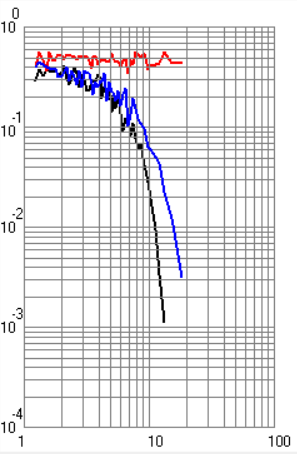
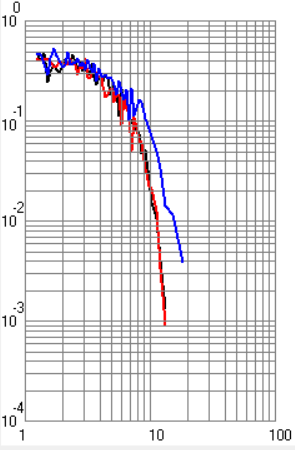
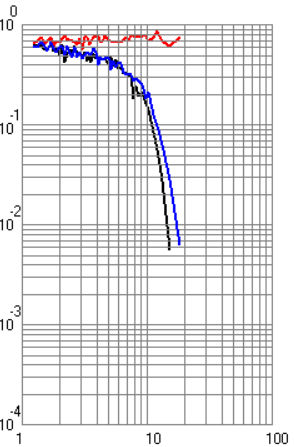
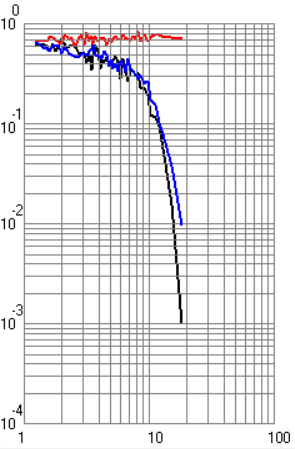
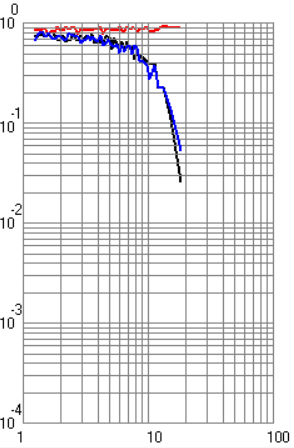
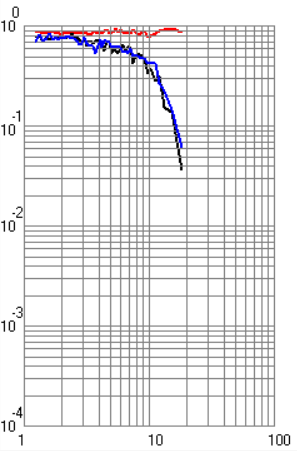
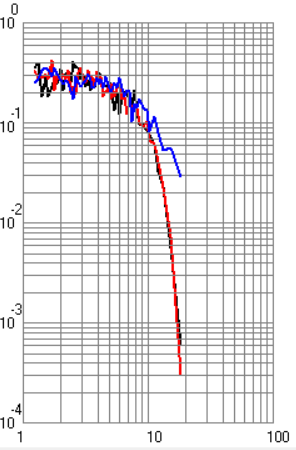
ФАКУЛЬТЕТ РАДИОЭЛЕКТРОНИКА И ЛАЗЕРНАЯ ТЕХНИКА КАФЕДРА РАДИОЭЛЕКТРОННЫЕ СИСТЕМЫ И УСТРОЙСТВА Лабораторная работа №2 по дисциплине «Основы теории и техники радиосистем передачи информации» по теме «Исследование помехоустойчивости систем радиопередачи информации» Выполнили студенты группы Беляков А.Б. ____________ РЛ1-92 (Подпись, дата) Карелин В.А. ____________ (Подпись, дата) Кудрова М.Д. ____________ (Подпись, дата) Проверил Семенов А.Н. ____________ (Подпись, дата) Москва 2021 г. Цель и задачи работы Цель работы – теоретическое и экспериментальное исследование помехоустойчивости радиосистем передачи информации. Задачи работы – ознакомление с теоретическим материалом по данным методическим указаниям, выполнение работы в указанном порядке. Назначение лабораторной работы – углубление теоретических знаний, практических умений и навыков в результате проведения экспериментальных исследований помехоустойчивости радиосистем передачи информации. Экспериментальная часть Экспериментальная установка состоит из персонального компьютера и программного обеспечения. Исследование характеристик системы передачи дискретной информации (СППИ) проводится путем математического моделирования устройств формирования и обработки сигналов, а также непрерывного какала связи (НКС). Непрерывный канал связи в общем виде содержит элементы, вносящие частотные и нелинейные искажения, аддитивный шум и мультипликационную помеху. На входе канала формируется полезный сигнал в соответствии с выбранным видом модуляции. Демодулятор представляет собой оптимальный приемник, содержащий m корреляторов и схему выбора максимума. Программное обеспечение позволяет получить временное представление сигналов в различных точках канала и демодулятора. Программа позволяет строить графики для различных видов сигналов. Под графиками подразумеваются: временной вид сигнала, вероятностные характеристики, виды сигнала после перемножителя и интегратора при наличии помех и искажений в канале. Также необходимо было убедиться в том, что фаза находится в «0». В ходе лабораторной работы были получены следующие экспериментальные графики (рисунки 1 – 8) для разных типов манипуляций. По умолчанию графики строятся для случая когерентного приема. Черная кривая соответствует вероятности ошибки при белом шуме, красная – при гармонической помехе, синяя – при рэлеевских замираниях.
Ответы на контрольные вопросы 1. Сформулируйте задачу различения m сигналов Пусть колебание на входе приёмника является суммой помехи и одного из сигналов 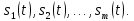 Задача состоит в том, чтобы по принятой реализации Задача состоит в том, чтобы по принятой реализации 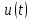 в условиях помех решить какой из сигналов был принят. в условиях помех решить какой из сигналов был принят.2. Поясните алгоритм работы оптимального демодулятора m детерминированных сигналов при когерентном и некогерентном методах приема. Демодулятор представляет собой оптимальный приемник, содержащий m корреляторов и схему выбора максимума. В случае некогерентного накопления принятый сигнал разбивается на квадратуры и высчитывается корреляционный интеграл от обоих квадратур. Далее идет усреднение сигнала по фазовой составляющей: корень от суммы квадратов действующей и мнимой части сигнала поступает в схему накопления. Для когерентной обработки необходимо обеспечить фазовую синхронизацию приемника с генератором сигнала передатчика, так как принцип когерентной обработки требует учитывать информацию о начальной фазе принятого сигнала. 3. Как найти вероятность ошибки в двоичных РСПИ? Вероятность ошибки при двоичной передаче и когерентном приеме 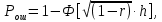 где 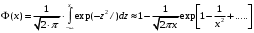 . .При двоичной передаче и некогерентном приеме ортогональных сигналов (λ 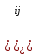 = 0). = 0). 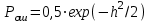 . .В системах с фазовой модуляцией (ФМ) и противоположными сигналами (А = -1) для устранения "обратной работы", связанной с неоднозначным определением фазы несущего колебания, используют методы относительной фазовой модуляции (ОФМ) с когерентной и некогерентной обработкой. В этом случае для когерентного приёма 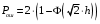 , а для некогерентного приёма , а для некогерентного приёма 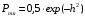 . .4.Как найти вероятность ошибки в многопозиционных РСПИ? Для многопозиционных систем передачи информации средняя вероятность ошибки находится усреднением по ансамблю сигналов: 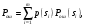 где p(si) – вероятность передачи сигнала si(t), Pош(si) – вероятность ошибки при передаче сигнала si(t). При использовании АФМ-сигналов ее вычисление в общем случае является весьма громоздким. Решение задачи упрощается при больших отношениях сигнал-шум. При этом можно воспользоваться верхней границей для вероятности ошибки 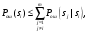 где Pош(si|si) – вероятность принятия решения в пользу сообщения si(t) при передаче сообщения si(t). При работе системы в условиях действия гауссовского белого шума с односторонней спектральной плотностью N0 вероятность ошибки, выраженная через расстояние d(si, sj), находится по формуле 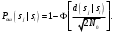 Тогда 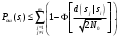 Используя асимптотическое представление интеграла вероятности, можно записать: 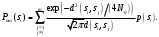 Соответственно, средняя вероятность ошибки имеет вид 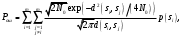 что дает удовлетворительную точность при Pош <0,01. Расчеты показывают, что при т ≥ 8 системы с АФМ-сигналами обладают более высокой помехоустойчивостью, чем m-ичные системы с фазовой манипуляцией. Например, при Pош = 10–5 и m = 8 проигрыш в средней энергии системы с фазовой манипуляцией по сравнению с системой, использующей оптимальный ансамбль АФМ сигналов, составляет 1,7 дБ, при m = 16 — 4,3 дБ, при m = 32 — 7,1 дБ, при m = 64 — 10,1 дБ, при т = 128 — 13,1 дБ. Многие из известных ансамблей АФМ-сигналов, построенных на основе треугольной и квадратной сетей, и ансамблей с круговым расположением сигнальных точек практически обеспечивают одинаковую помехоустойчивость. По крайней мере, могут быть построены различные типы систем АФМ-сигналов, проигрыш которых в средней энергии по сравнению с оптимальными системами не будет превышать 0,5 дБ. Это позволяет выбирать сигналы, для которых реализация модулятора и демодулятора не вызывает трудностей. 5. Сравните помехоустойчивость двоичных и многопозиционных РСПИ Для канала с релеевскими замираниями и некогерентным приемом ЧМ сигналов помехоустойчивость определяется как: 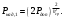 При заданных параметрах 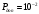 и и 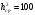 получаем: получаем: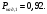 Помехоустойчивость для m-позиционного приема: 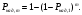 С ростом количества числа ветвей многопозиционного приема помехоустойчивость будет расти: 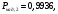 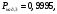 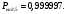 На практике, как правило, используют двух- или трехпозиционный прием, так как с увеличением каналов выигрыш в помехоустойчивости уменьшается. 6. Изобразите структурные схемы оптимальных различителей сигналов ФМ-2, ФМ-4, ФМ-8 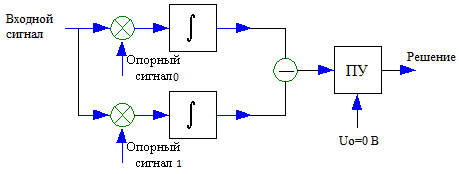 Рисунок 9 – Оптимальный корреляционный различитель ФМ-2 сигналов 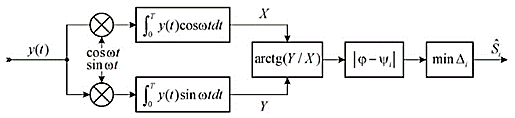 Рисунок 1 – Оптимальный корреляционный различитель ФМ-m сигналов Для обеспечения возможности различения сигналов с фазовой манипуляцией необходимо использовать фазовую синхронизацию опорных сигналов с генератором принимаемых сигналов. 7. Изобразите структурные схемы оптимальных различителей сигналов ЧМ, АМ, ОФМ при некогерентном приеме. 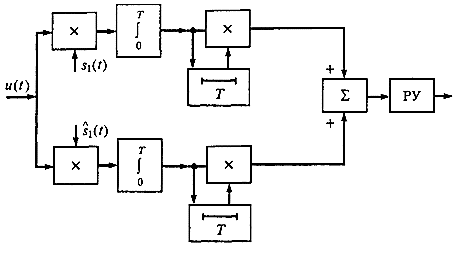 Рисунок 2 – Оптимальный различитель ОФМ сигналов 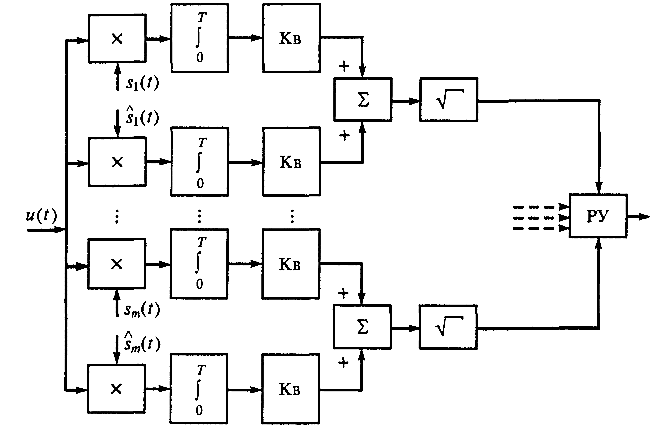 Рисунок 3 – Оптимальный корреляционный различитель АМ и ЧМ сигналов Различие оптимальных различителей для АМ и ЧМ сигналов заключается в различных опорных сигналах, подаваемых на перемножители. Домашнее задание Определите среднюю вероятность ошибки ФМ сигналов при когерентном приеме в условиях рэлеевских замираний. M – коэффициент передачи канала, так как изменения симметричным образом, то введём условие вероятности ошибки 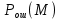 . . 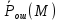 – задаём количество перед информации, надёжность по помехоустойчивости – задаём количество перед информации, надёжность по помехоустойчивости 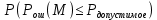 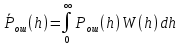 при релеевском замирании: 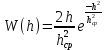 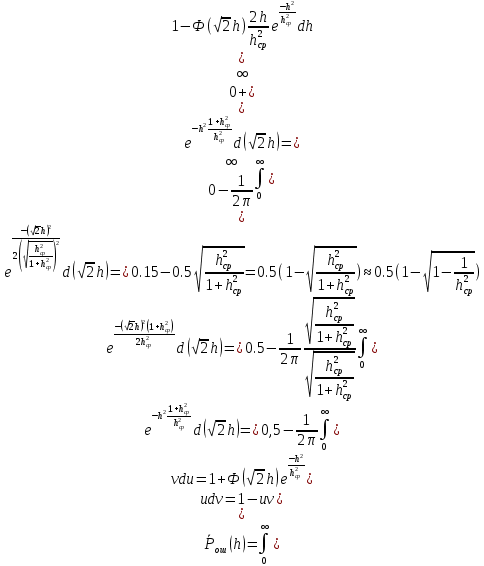 В соответствии с разложением по биному 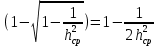 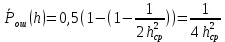 |