Курсавая РТС. Курсач Радиотехнические средства. Исследование принципа работы алгоритма цифровой демодуляции сигналов с четырехкратной
 Скачать 0.87 Mb. Скачать 0.87 Mb.
|
|
ИССЛЕДОВАНИЕ ПРИНЦИПА РАБОТЫ АЛГОРИТМА ЦИФРОВОЙ ДЕМОДУЛЯЦИИ СИГНАЛОВ С ЧЕТЫРЕХКРАТНОЙ ФАЗОВОЙ МАНИПУЛЯЦИЕЙ Введение. Развитие методов построения универсальных и специализированных алгоритмов и устройств цифровой обработки модулированных радиосигналов связано с необходимостью оптимизации их работы, повышения быстродействия и помехоустойчивости. Фазовая манипуляция (ФМн или PSK) обеспечивает высокую помехоустойчивость, особенно при когерентной демодуляции, а многопозиционная ФМн позволяет повысить скорость передачи информации. Предлагаемый алгоритм цифрового устройства демодуляции фазоманипулированных сигналов вдвое увеличивает скорость обработки принимаемого сигнала за счет увеличения количества одновременно обрабатываемых отсчетов. На рис. 1 приведена структурная схема быстрого цифрового алгоритма когерентной демодуляции сигнала с четырехкратной ФМн (QPSK) с начальными фазами ψ=0, ψ=π/2, ψ=π и ψ=3π/2. 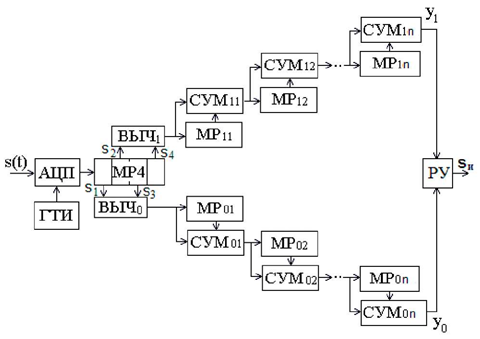 Рис. 1. Структурная схема алгоритма демодуляции На каждый i-й период длительностью T0 сигнала формируются по четыре отсчета s1, s2, s3 и s4, как в синхронном режиме показано на рис. 2 при начальной фазе ψ=0 (рис. 2, а) или ψ=3π/2 (рис. 2, б). 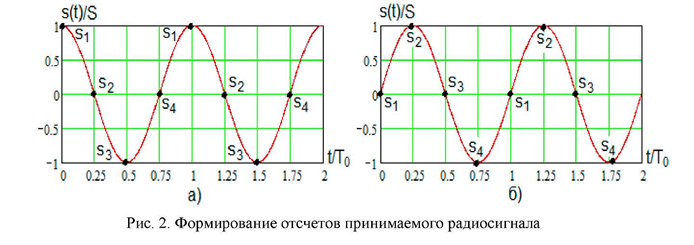 Нечетные отсчеты s1 и s3 поступают в устройство вычитания ВЫЧ0, а четные s2 и s4 — в ВЫЧ1, после чего выполняется интенсивное накопление разностей s1 - s3 и s2 - s4 за N периодов. В результате данной операции формируются отклики y0i и y1i: s1, s2, s3 и s4, как в синхронном режиме показано на рис. 2 при начальной фазе Один из откликов после приема элемента длительностью NT0 при отсутствии помех равен ±2NS, а другой в этом случае равен нулю. В рассматриваемом устройстве демодуляции реализуется два квадратурных канала обработки y0 и y1, сдвиг относительно времени между четными и нечетными отсчетами составляет 1/4 периода ВЧ сигнала, или 90° по фазе. Фазоманипулированный сигнал после модуляции можно записать в виде где xk — информационный символ со значениями 0, 1, 2 и 3, ]t/NT0[ – целая часть числа, равная номеру k информационного символа, начальная фаза ФМ сигнала принимает значение В результате моделирования получаем зависимости нормированных откликов y0/2N (пунктир) и y1/2N (сплошная линия) от номера текущего информационного символа k, показаны на рис. 3. Модулирующий сигнал показан точками xk/3. 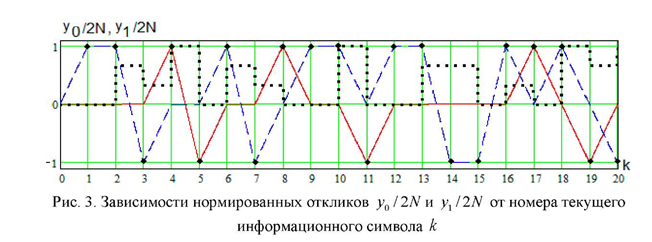 Фазе ψ=0 соответствует значение y0/2N=1, ψ=π – соответственно y0/2N=-1, а величина y1/2N=0, как показано пунктиром на рис. 3. Аналогично при ψ=π/2 имеем y1/2N=1, при ψ=3π/2 – соответственно y1/2N=-1, y0/2N=0 (сплошная линия на рис. 3). Об оптимальности алгоритма обработки сигнала свидетельствует пилообразная форма отклика демодулятора. В решающем устройстве (РУ) (рис. 1) формируется решение о принятом информационном сигнале sИ путем сравнения модулей откликов y0 и y1 друг с другом. Примеры полученных в результате моделирования реализаций откликов y0 и y1 при наличии белого шума и N = 256 показаны сплошными линиями на рис. 4 (i— номер периода, i/N — номер символа). Пунктиром показаны значения xk/3. Точками на рис. 4 отмечены значения откликов, по которым принимаются решения о передаваемом символе. 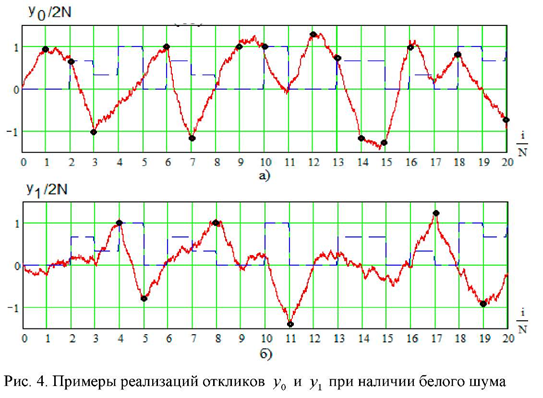 Сигнальная и шумовая составляющие имеют достаточно сглаженный вид, что, в свою очередь, дает информацию о свойствах хорошего фильтра данного алгоритма. Демодулятор сигналов с четырехкратной ФМн формирует два значения y0 (1) и y1 (2), при анализе которых формируется решение о принятом информационном символе. Плотности вероятностей значений y: w0(y) или w1(y) для y0 или y1 в канале с сигналом имеют вид 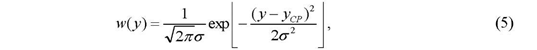 а в канале с шумом 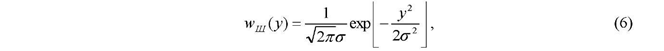 графическое представление плотностей вероятности показано на рис. 5. 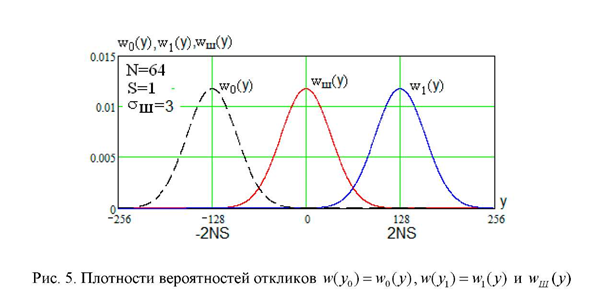 Сигналы с четырехкратной ФМ образуют неэквидистантную биортогональную систему [1]. Согласно описанному выше принципу работы решающего устройства, если |у0| > |у1|, то плотность вероятностей вычисляется по формуле (5), и ее график показан на рис. 6 для значений ψ=0 или ψ=π. 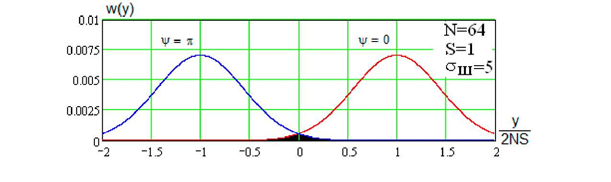 Рис. 6. Плотность вероятностей откликов для значений ψ=0 или ψ=π Тогда для плотности вероятностей z=|y| в канале с сигналом с учетом того, что обратная функция двухзначна, можно записать [2] 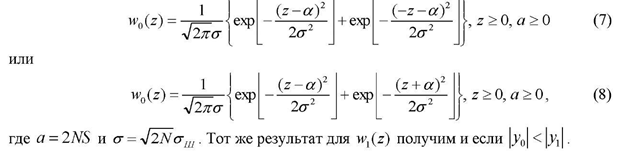 где a=2NS и В канале с шумом выражение для плотности вероятностей величины z = |y| следует из (8) при a = 0 и имеет вид 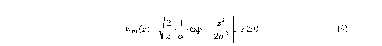 Вероятность q1 правильного решения в канале с сигналом равна 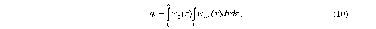 Подставляя (8) и (9), получим 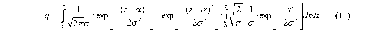 Введем обозначения 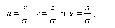 тогда 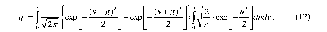 а после преобразований получим 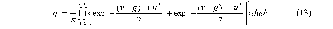 или 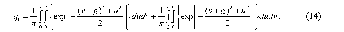 Проведем в (13) замену переменных 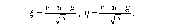 тогда 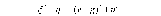 и первый интеграл в (14) согласно [1] преобразуется к виду 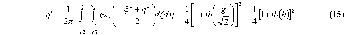 где Ф(х) — функция Крампа, равная 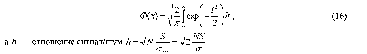 Аналогично для второго слагаемого в (14) при замене 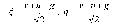 получим 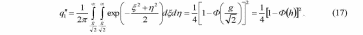 В результате согласно (14) вероятность q1 правильного выбора канала с сигналом равна 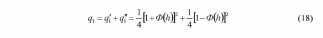 или 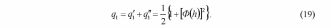 Величина q1" много меньше q1' тогда приближенно получим 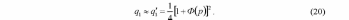 Выражение (20) получено в [1] качестве вероятности приема сигнала с четырехкратной ФМн без ошибки при его согласованной фильтрации. После обнаружения канала с сигналом делается вывод о знаке его отклика и вероятность верного приема такого символа будет равна 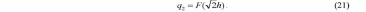 Вероятность верной демодуляцииq равна 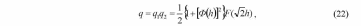 при этом вероятность ошибки 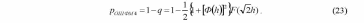 Зависимость рошфм4 (23) от отношения сигнал/шумh (в дБ) представлена на рис. 7 (верхняя сплошная кривая). Пунктиром показана зависимостьрош (h) для двоичного сигнала. 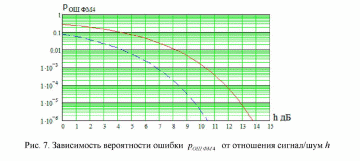 Заключение. Анализируя рис. 7, можно сделать вывод о том, что предлагаемый алгоритм демодуляции сигналов с четырехкратной фазовой манипуляцией является оптимальным, уступая алгоритму демодуляции двоичных фазоманипулированных сигналов примерно 3 дБ, но необходимо учитывать, что в данном случае скорость обработки сигналов в два раза больше. Представленные в статье расчеты и результаты моделирования свидетельствуют о том, что предлагаемый цифровой алгоритм демодуляции четырехпозиционных фазоманипулированных сигналов и устройство, его реализующее, являются оптимальными. |
