Исследование распределения магнитного поля вдоль оси соленоида. 05194-1 Ковригин Н Исследование распределения магнитного поля вд. Исследование распределения магнитного поля вдоль оси соленоида Студент группы 051941 Ковригин Н. Д. Проверил
 Скачать 251.45 Kb. Скачать 251.45 Kb.
|
|
ННГУ им. Н. И. Лобачевского Физический факультет Отчёт по лабораторной работе Исследование распределения магнитного поля вдоль оси соленоида Выполнил: Студент группы 05194-1 Ковригин Н. Д. Проверил: Сомов Н. В. Нижний Новгород 2020 Цель работы Изучить распределение магнитного поля вдоль оси соленоида с помощью датчика Холла. Теоретическая часть Цилиндрическая проволочная катушка с намотанными вдоль неё витками проволоки называется соленоидом. Если витков много и они намотаны достаточно плотно, то катушку можно представить в виде совокупности колец с током. Определим магнитную индукцию на оси одного витка (рис.1): 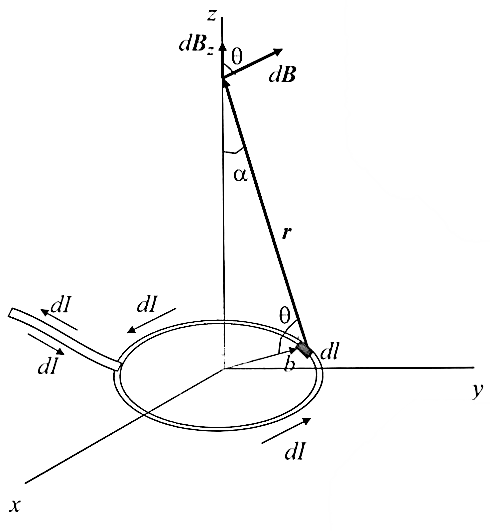 Рис. 1. Поле на оси кольца. Для линейного элемента dl тока dI по закону Био-Савара магнитная индукция определяется по формуле: 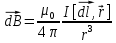 (1) (1)Разложим поле на две составляющие: осевую dBz и dBr радиальную. В силу симметрии задачи поле в точке наблюдения направлено вдоль оси z: 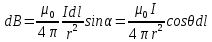 (2) (2)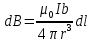 (3) (3) Проинтегрируем (3) по круговому контуру l: 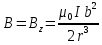 (4) (4)Возьмём (4) за основу и вычислим магнитную индукцию в любой точке z на оси катушки L. 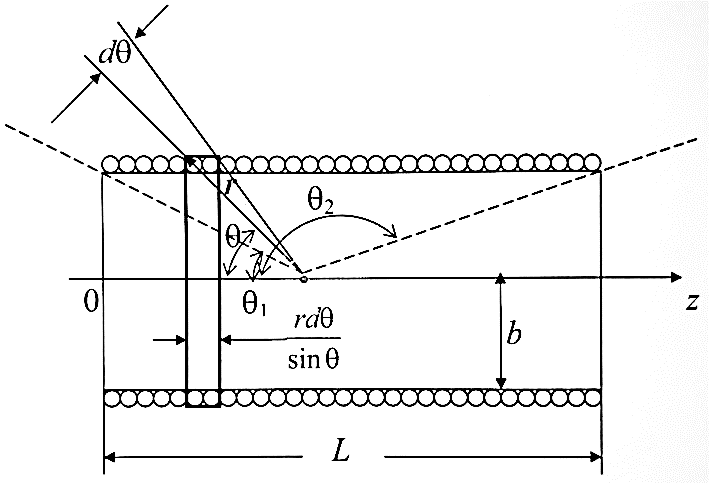 Рис. 2. Поле на оси соленоида. Рассмотрим вклад колец с током, видимых из точки наблюдения z под углом d на оси катушки: n0 – число витков на 1 см длины. 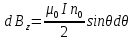 (5) (5)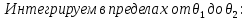 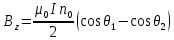 (6) (6)где 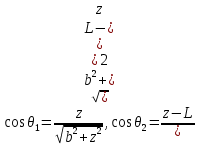 (7) (7)Для измерения 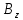 на оси катушки используется датчик Холла – однородная проводящая пластина, вдоль которой течет ток I: на оси катушки используется датчик Холла – однородная проводящая пластина, вдоль которой течет ток I: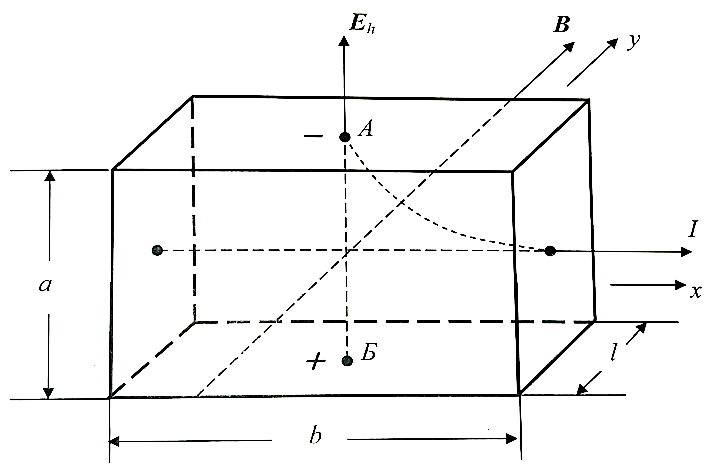 Рис. 3. Датчик Холла. Поместим пластинку в магнитное поле; на движущийся в магнитном поле заряд действует сила Лоренца: 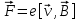 (8) (8)e – величина заряда, 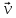 – его скорость, – его скорость, 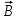 – индукция магнитного поля. – индукция магнитного поля.Магнитное поле, в котором радиус кривизны траектории окажется много больше длины свободного пробега электрона, называется слабым. В таком поле 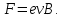 Eh – напряженность этого поля, UAB – разность потенциалов между гранями А и Б. Eh – напряженность этого поля, UAB – разность потенциалов между гранями А и Б.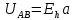 . (9) . (9)В стационарном состоянии 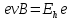 , тогда: , тогда: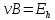 (10) (10)Для электронного полупроводника или металла 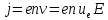 – плотность тока в образце, – плотность тока в образце,где n – концентрация электронов, 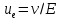 – подвижность электронов в электрическом поле. – подвижность электронов в электрическом поле.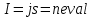 (11) (11)Решаем систему (8), (9), (10) и найдем ЭДС Холла: 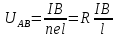 (12) (12)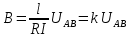 (13) (13)где 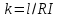 – константа при заданном I. – константа при заданном I.Поместив холловский датчик в магнитное поле, получаем возможность измерить его магнитную индукцию в данной точке. Перемещая датчик вдоль оси соленоида, можно получить распределение магнитной индукции вдоль оси соленоида по всей его длине. Экспериментальная часть Были выбраны приборы: Источник тока Вольтметр (Umax = 15 мВ, класс точности – 0.2) Соленоид (L = 200 мм, n0 = 275 см-1) Начало отсчета находится в середине соленоида. Установим на источнике питания I = 2A – значение тока, протекающего через соленоид. Проведя трижды измерения ЭДС Холла вдоль оси соленоида, получили следующие результаты: Таблица 1. Результаты измерений
где 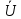 – среднее статистическое результатов измерений, полученные по формуле – среднее статистическое результатов измерений, полученные по формуле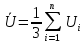 (14) (14)где n – количество измерений. Вычислим абсолютную погрешность измерений. Нам понадобятся формулы из [2]: 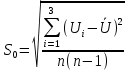 (15) (15)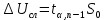 (16) (16)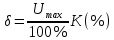 (17) (17)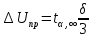 (18) (18)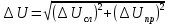 (19) (19)где 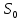 – среднеквадратичное отклонение среднего значения, – среднеквадратичное отклонение среднего значения, 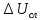 - случайная погрешность измерений, - случайная погрешность измерений, 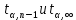 коэффициенты Стьюдента, α – доверительная вероятность коэффициенты Стьюдента, α – доверительная вероятность 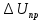 – приборная погрешность, – приборная погрешность, 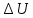 – абсолютная погрешность. – абсолютная погрешность.Примем доверительную вероятность α = 0.95. Составим таблицу для ЭДС Холла с учетом абсолютной погрешности. В качестве начала отсчета выберем один из концов соленоида: Таблица 2. ЭДС Холла с учетом абсолютной погрешности
Вычислим теоретическое распределение магнитной индукции 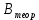 вдоль оси соленоида по формуле (6). вдоль оси соленоида по формуле (6). Погрешность, как косвенную, вычислим по формуле: 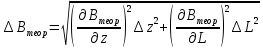 (20) (20)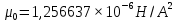 . В итоге получим следующие результаты: . В итоге получим следующие результаты:Таблица 3. Теоретическое распределение магнитной индукции вдоль оси соленоида.
Найдём постоянную k и ее погрешность: 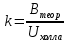 (21) (21)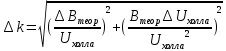 (22) (22)Таблица 4. Значение постоянной k и ее погрешности.
Вычислим постоянную k и ее погрешность, как среднее значение: 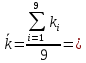 42 мТл/В. (23) 42 мТл/В. (23) 3 мТл/В. (24) 3 мТл/В. (24)Вычислим экспериментальное распределение магнитной индукции вдоль оси соленоида по формуле (13). Погрешность вычислим по формуле: 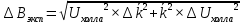 (25) (25)Таблица 5. Экспериментальное распределение магнитной индукции вдоль оси соленоида.
Нанесём на график расчетную кривую зависимостей Bтеор и экспериментальные точки Bэксп: 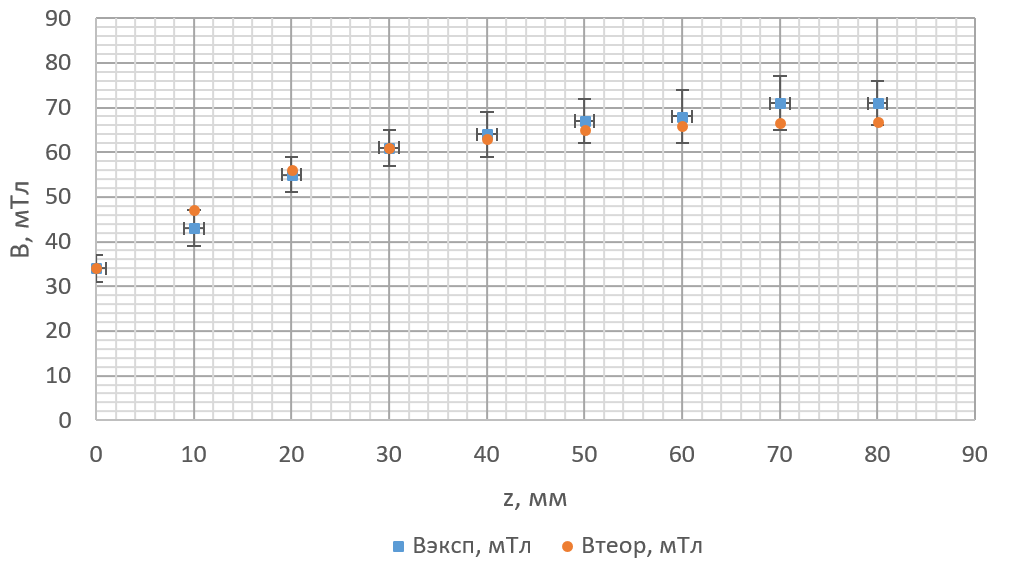 Вывод В данной лабораторной работе было изучено распределение магнитной индукции вдоль оси соленоида с помощью датчика Холла. Были получены теоретические и экспериментальные значения и построен график зависимости B(z). Значения равны друг другу в пределах погрешностей. Также было подтверждено значение постоянной k = 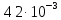 Список используемых источников Доброхотов Э. В. «Исследование распределения магнитного поля вдоль оси соленоида»: Нижний Новгород: Нижегородский госуниверситет, 2016. – 8 с. Фаддеев М.А. «Элементарная обработка результатов эксперимента»: Учебное пособие. – Нижний Новгород: Издательство Нижегородского госуниверситета, 2002. – 108 с. |

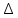 Bтеор, мТл
Bтеор, мТл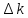 , мТл/В
, мТл/В