Исследование разомкнутой линейной системы. Исследование разомкнутой линейной системы
 Скачать 71.6 Kb. Скачать 71.6 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» Факультет: «Машиностроения» Кафедра: «Автоматика и управление» Лабораторная работа №1 По дисциплине «Проектирование систем управления» На тему «Исследование разомкнутой линейной системы» Выполнил студент группы 191-251 Булыгин.К.Д. /__________/ Проверил: Березин Е. С. /__________/ Москва 2022 г. Теоретическая часть Для описания линейных систем могут применяться несколько способов: дифференциальные уравнения модели в пространстве состояний передаточные функции модели вида «нули-полюса» Первые два способа называются временны, поскольку описывают поведение системы во временной области и отражают внутренние связи между сигналами. Передаточные функции и модели вида «нули-полюса» относятся к частотным способам описания, так как непосредственно связаны с частотными характеристиками системы и отражают только вход-выходные свойства (то есть, описывают динамику не полностью). Частотные методы позволяют применять для анализа и синтеза алгебраические методы, что часто упрощает расчеты. С другой стороны, для автоматических вычислений более пригодны методы, основанные на моделях в пространстве состояний, поскольку они используют вычислительно устойчивые алгоритмы линейной алгебры. Исходные уравнения динамики объектов, которые строятся на основе законов физики, имеют вид нелинейных дифференциальных уравнений. Для приближенного анализа и синтеза обычно проводят их линеаризацию в окрестности установившегося режима и получают линейные дифференциальные уравнения. Передаточная функция в среде MATLAB вводится в виде отношения двух многочленов (полиномов) от комплексной переменной s. Полиномы хранятся как массивы коэффициентов, записанных по убыванию степеней. Нулями называются корни числителя, полюсами – корни знаменателя. Импульсной характеристикой (весовой функцией) w(t) называется реакция системы на единичный бесконечный импульс (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Практическая часть Вариант 4 Описание системы Исследуется система, описываемая математической моделью в виде передаточной функции 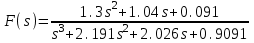 Результаты исследования адрес файла tf.m: C:\Program Files (x86)\MATLAB\R2009b\toolbox\control\control\@tf\tf.m % tf constructor нули передаточной функции -0.7000 -0.1000 полюса передаточной функции -1.1001 + 0.0000i -0.5454 + 0.7273i -0.5454 – 0.7273i коэффициент усиления звена в установившемся режиме k = 0.1001 полоса пропускания системы b = 18.3381 рад/сек A = -2.191 -2.026 -0.9091 1 0 0 0 1 0 b = 2 0 0 c = 0.65 0.52 0.0455 d = 0 статический коэффициент усиления после изменения матрицы 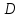 k1 = 1.1001 связь между k и k1 объясняется тем, что размерность этой величины равна отношению размерностей сигналов выхода и выхода. модель в форме «нули-полюса» 1.3 (s+0.7) (s+0.1) ------------------------------- (s+1.1) (s^2 + 1.091s + 0.8264) коэффициенты демпфирования и частоты среза
Импульсные характеристики систем f и f_ss получились, одинаковые, потому что импульсная характеристика отражает лишь вход-выходные соотношения при нулевых начальных условиях, то есть не может полностью описывать динамику системы. Переходные процессы исходной и модифицированной систем 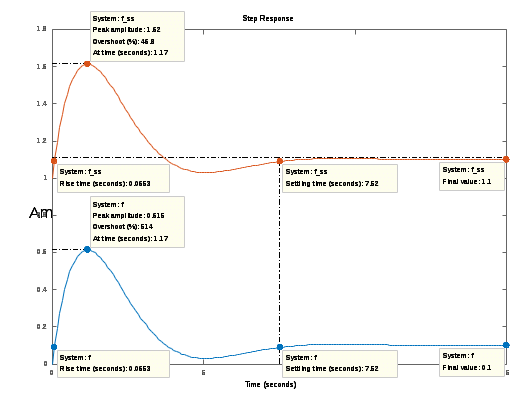 амплитудная частотная характеристика 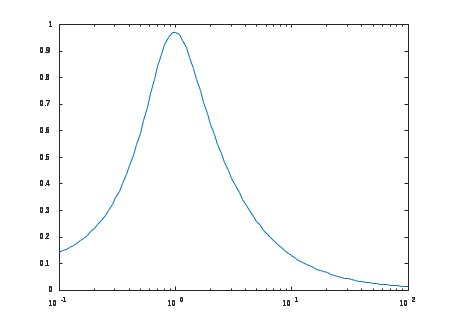 для того, чтобы найти статический коэффициент усиления по АЧХ, надо найти предельное значение переходной функции. для того, чтобы найти полосу пропускания по АЧХ, надо найти диапазон частот, в пределах которого АЧХ достаточно равномерна. реакция на сигнал, состоящий из прямоугольных импульсов 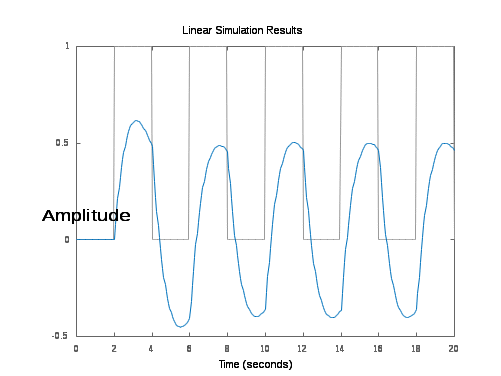 Вывод: я исследовал систему, описанную моделью в передаточной функции, с помощью среды Matlab, нашёл нули и полюса этой функции, а также различные коэффициенты. Построил графики переходных процессов, амплитудную частотную характеристику и реакцию системы на сигнал прямоугольных импульсов. |
