Проектирование систем управление Березин. ЛР1. Исследование разомкнутой линейной системы
 Скачать 1.33 Mb. Скачать 1.33 Mb.
|
|
МИНИСТРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РФ Федеральное государственное автономное образовательное учреждение высшего образования «МОСКОВСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» (ФГАОУ ВО «Московский Политех»)  Факультет: «Машиностроение» Кафедра: «Автоматика и управление» Дисциплина: «Проектирование систем управления» Отчёт по лабораторной работе №1 Тема: «Исследование разомкнутой линейной системы» Группа 201-251 Выполнил: Галеев Артем Булатович Проверил: Березин Евгений Сергеевич Москва 2023 Цель работы: освоение методов анализа одномерной линейной непрерывной системы с помощью среды Matlab Теоретическая часть: Модели линейных систем Для описания линейных систем могут применяться несколько способов: дифференциальные уравнения модели в пространстве состояний передаточные функции модели вида «нули-полюса» Коэффициент усиления в установившемся режиме Одна из важнейших характеристик линейной системы – коэффициент усиления в установившемся режиме или статический коэффициент усилении (static gain, DC-gain). Его можно определить как установившееся значение сигнала выхода при постоянном входном сигнале, равном единице. Размерность этой величины равна отношению размерностей сигналов выхода и выхода. Импульсная характеристика Импульсной характеристикой (весовой функцией) называется реакция системы на единичный бесконечный импульс (дельта-функцию или функцию Дирака) при нулевых начальных условиях. Дельта-функция определяется равенствами 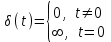 , , 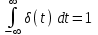 . .Это обобщенная функция – математический объект, представляющий собой идеальный сигнал, никакое реальное устройство не способно его воспроизвести. Дельта-функцию можно рассматривать как предел прямоугольного импульса единичной площади с центром в точке при стремлении ширины импульса к нулю. Переходная характеристика Переходной характеристикой (переходной функцией) называется реакция системы (при нулевых начальных условиях) на единичный ступенчатый сигнал (единичный скачок) Частотная характеристика При подаче на вход линейной системы гармонического (синусоидального) сигнала 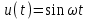 с частотой с частотой 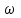 (она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы (она измеряется в радианах в секунду), на выходе будет также гармонический сигнал той же частоты, но другой амплитуды и фазы 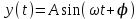 , где , где 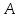 – амплитуда и – амплитуда и 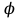 – сдвиг фазы. – сдвиг фазы.Частотная характеристика определяется как реакция системы на комплексный экспоненциальный сигнал 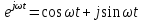 . Для ее построения надо использовать подстановку . Для ее построения надо использовать подстановку 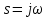 в передаточной функции в передаточной функции  . Выражение . Выражение 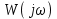 называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ). называется частотной передаточной функцией или амплитудно-фазовой частотной характеристикой системы (АФЧХ).Полюса и нули Многие динамические свойства системы (например, быстродействие, перерегулирование) определяются полюсами передаточной функции (или, что то же самое, собственными числами матрицы модели в пространстве состояний). Передаточную функцию можно записать как произведение передаточных функций элементарных звеньев первого и второго порядков. Таким образом, множество полюсов передаточной функции устойчивой системы составляют полюса передаточных функций двух типов простейших звеньев: апериодических и колебательных. Самостоятельная часть: Вариант 4
Исследуется система, описываемая математической моделью в виде передаточной функции 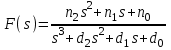 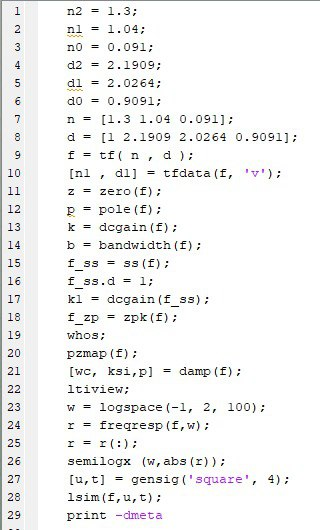 Рис. 1. Итоговая программа в среде MathLab 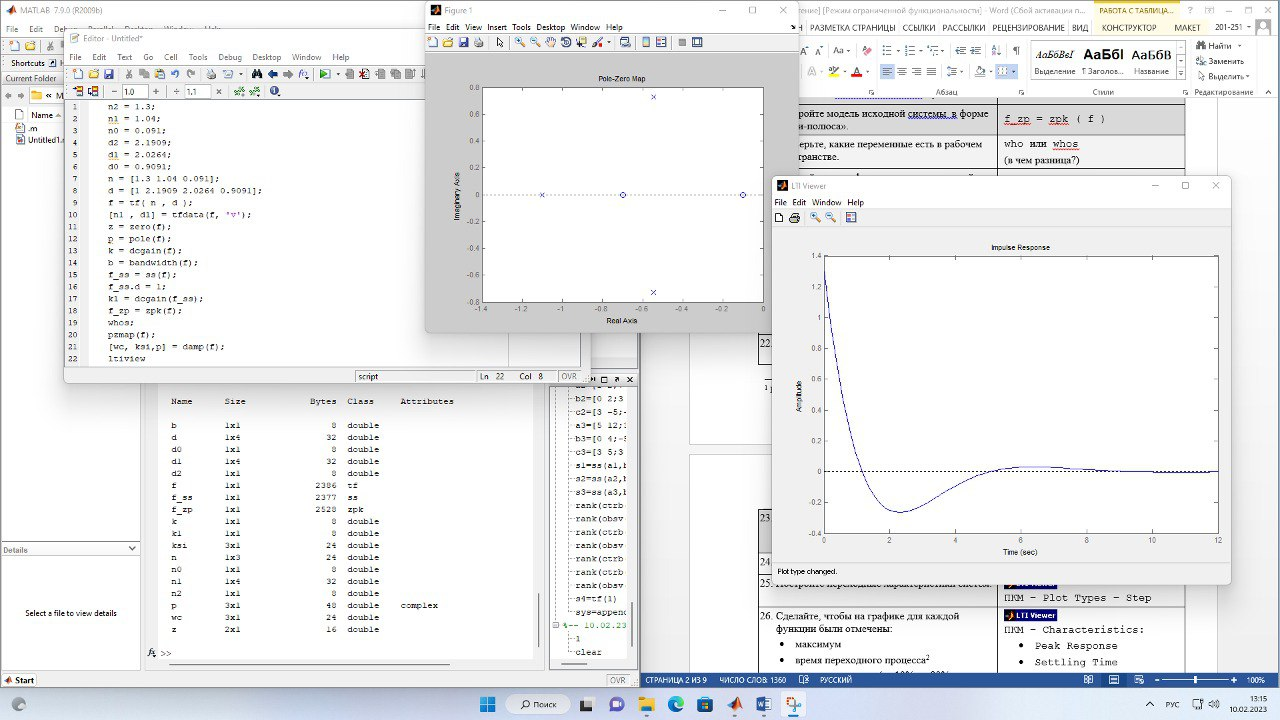 Рис. 2. Расположение нулей и полюсов системы(слева) и импульсная характеристика системы(справа) 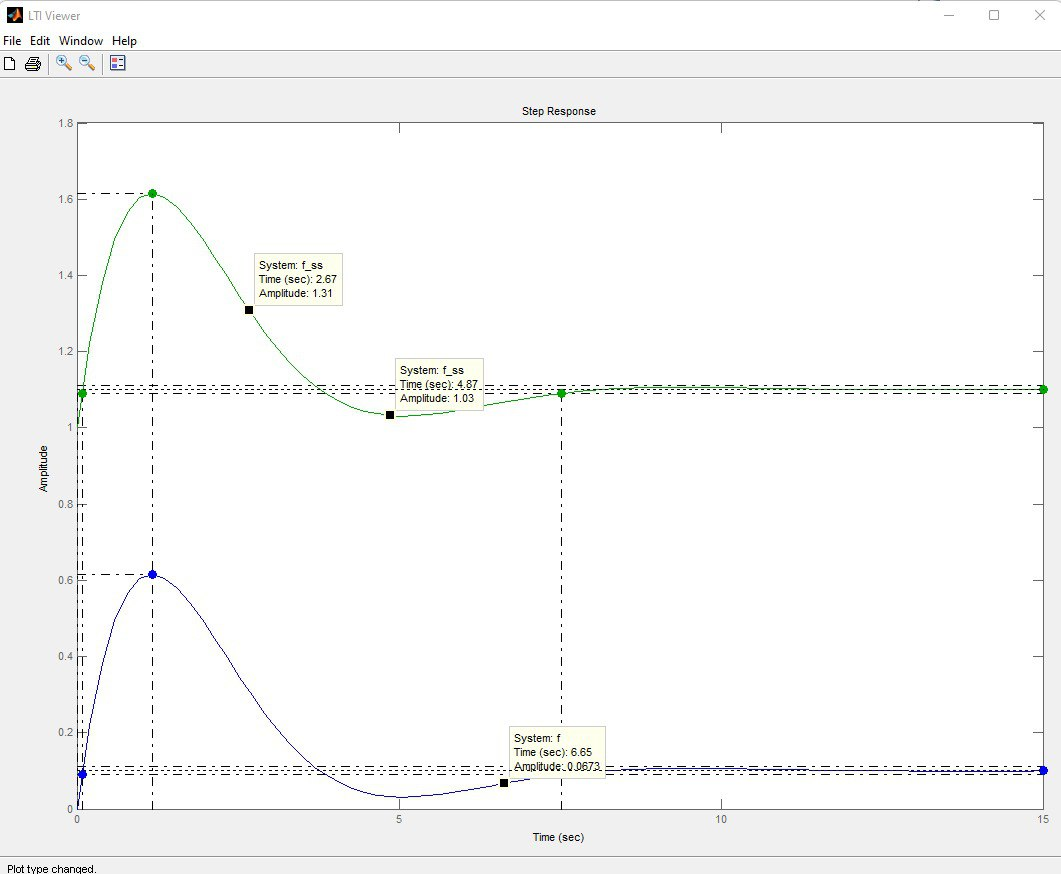 Рис. 3. Переходные характеристики систем 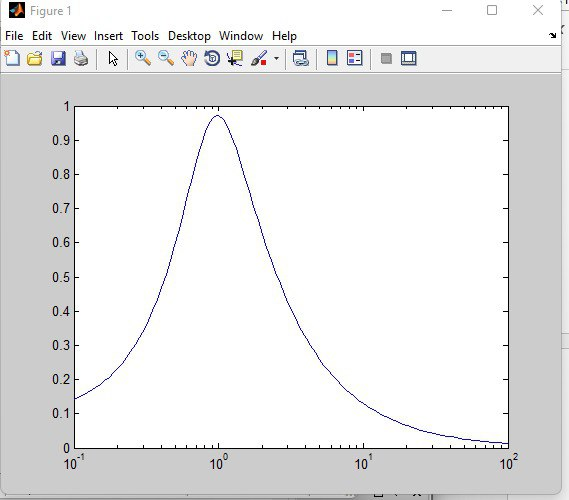 Рис. 4. Частотная характеристика исходной системы 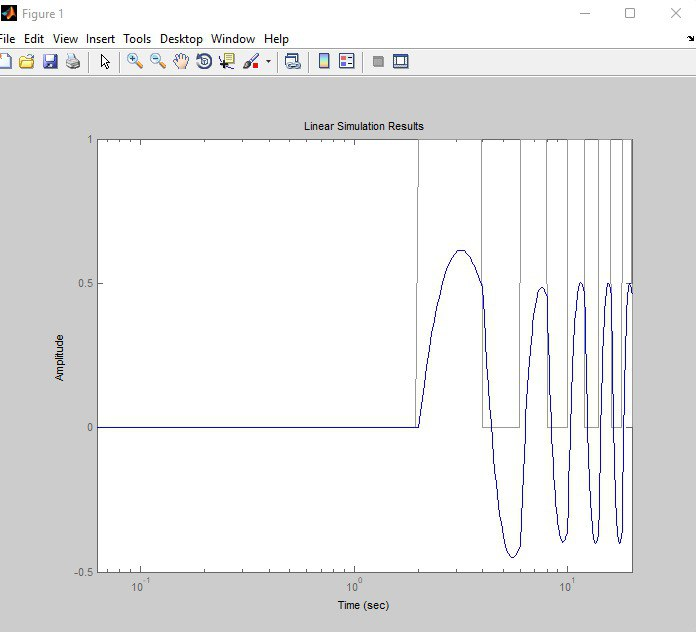 Рис. 5. Сигнал, имитирующий прямоугольные импульсы единичной амплитуды с периодом 4 секунды  Рис. 6. Сигнал выхода системы f при данном (Рис. 5) входе Вывод: В ходе данной лабораторной работы освоил методы анализа одномерной линейной непрерывной системы с помощью среды Matlab. |