ЛИНЕАРИЗАЦИЯ В ПРОСТРАНСТВЕ СОСТОЯНИЙ. ПР2_ТАУ. Цель работы Выполнение линеаризации в пространстве состояний для нелинейных функций и проверка результатов моделированием в MatLab Simulink. Исходные данные
 Скачать 313.88 Kb. Скачать 313.88 Kb.
|
|
Цель работы Выполнение линеаризации в пространстве состояний для нелинейных функций и проверка результатов моделированием в MatLab Simulink. Исходные данные Для двух вариантов нелинейных функций выполнить линеаризацию в пространстве состояний для двух различных рабочих точек. Проверить результат моделированием в MatLab Simulink. Вариант 5 – 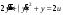 , , 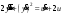 . .Расчетная часть Изначально будет выполнена линеаризация в пространстве состояний для первого варианта нелинейной функции для двух различных рабочих точек. 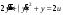 . .Во-первых, необходимо ввести переменные состояния: 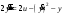 , ,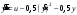 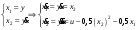 . .Нелинейные уравнения состояния примут вид: 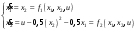 Следовательно, можно получить якобианы системы:  , ,  , ,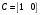 , , 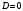 . .Линеаризация будет происходить в рабочих точках: 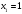 , , 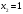 , , 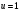 . .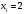 , , 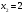 , , 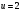 . .Тогда: 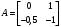 , , 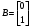 , , 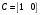 , , 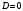 . .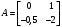 , , 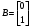 , , 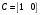 , , 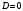 . .Проверка решения производится в MatLab Simulink. На рисунке 1 показана блок-схема сравнения исходной и линеаризованной системы, а на рисунке 2 и рисунке 3 – график переходных процессов.  Рисунок 1 – Блок-схема сравнения исходной и линеаризованной системы 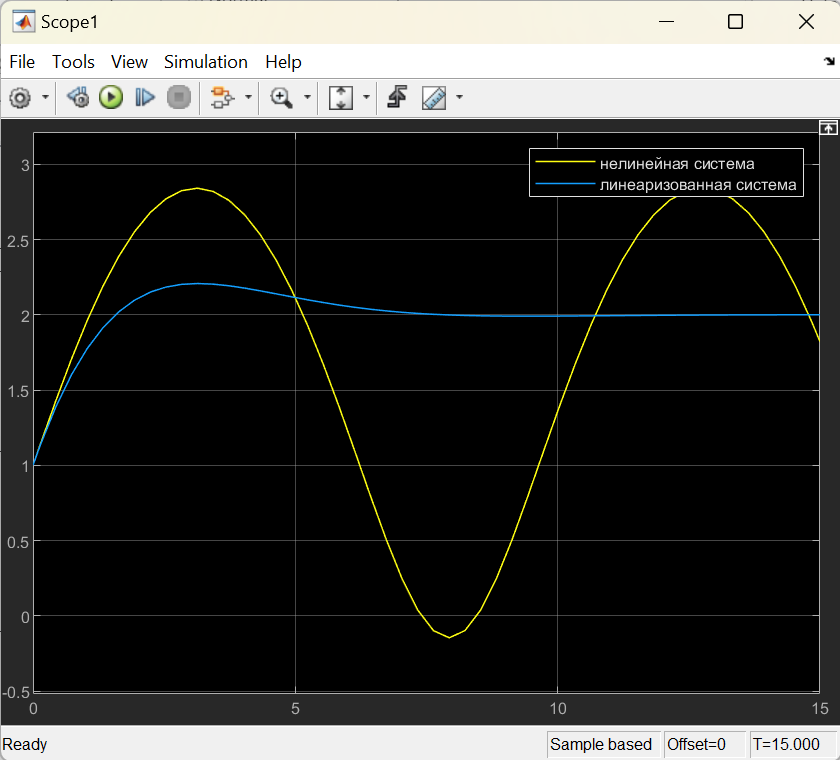 Рисунок 2 – График переходных процессов 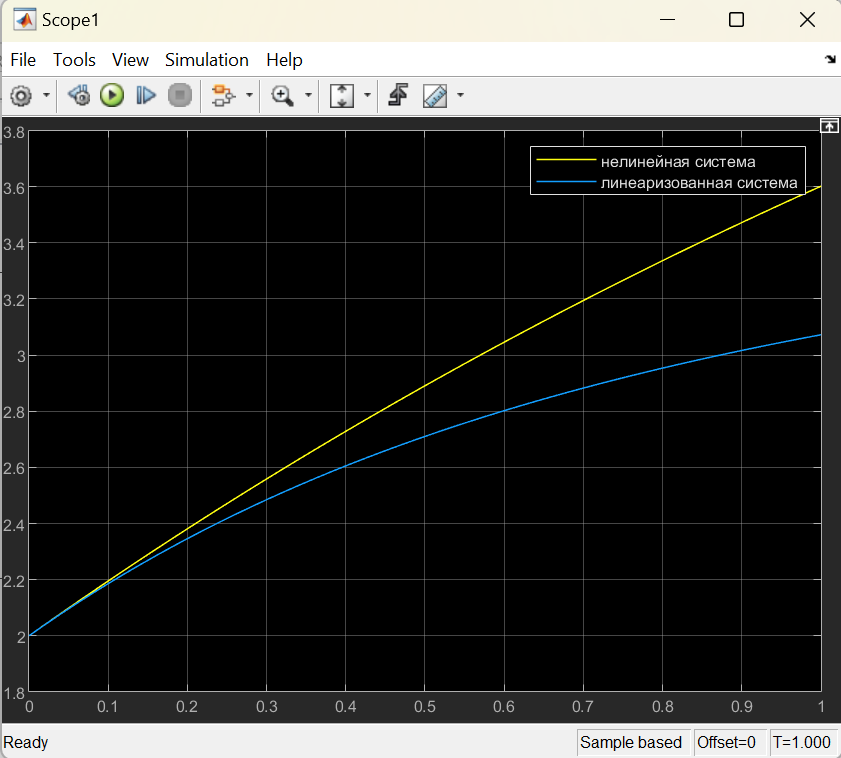 Рисунок 3 – График переходных процессов Теперь будет выполнена линеаризация в пространстве состояний для второго варианта нелинейной функции для двух различных рабочих точек. 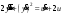 . .Во-первых, необходимо ввести переменные состояния: 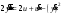 , ,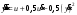 , , . .Нелинейные уравнения состояния примут вид: 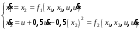 Следовательно, можно получить якобианы системы:  , , 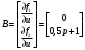 , ,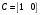 , , 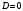 . .Линеаризация будет происходить в рабочих точках: 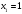 , , 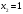 , , 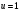 . .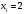 , , 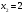 , , 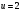 . .Тогда: 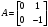 , , 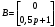 , , 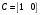 , , 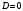 . .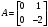 , , 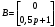 , , 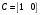 , , 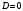 . .Проверка решения производится в MatLab Simulink. На рисунке 4 показана блок-схема сравнения исходной и линеаризованной системы, а на рисунке 5 и рисунке 6 – график переходных процессов. 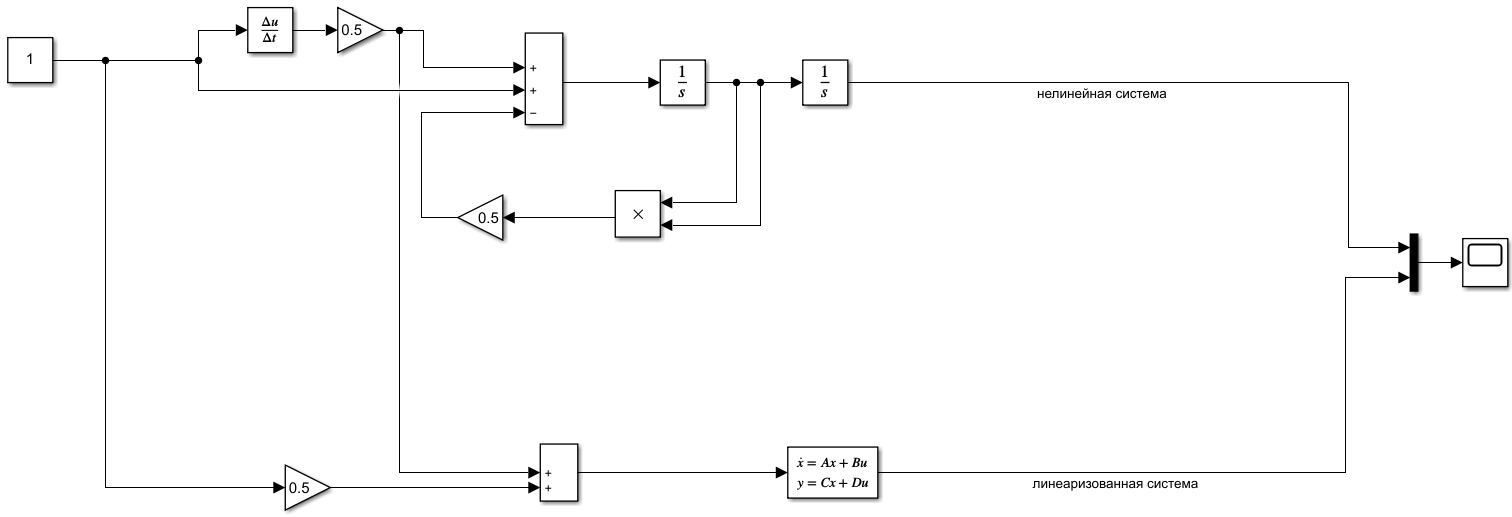 Рисунок 4 – Блок-схема сравнения исходной и линеаризованной системы 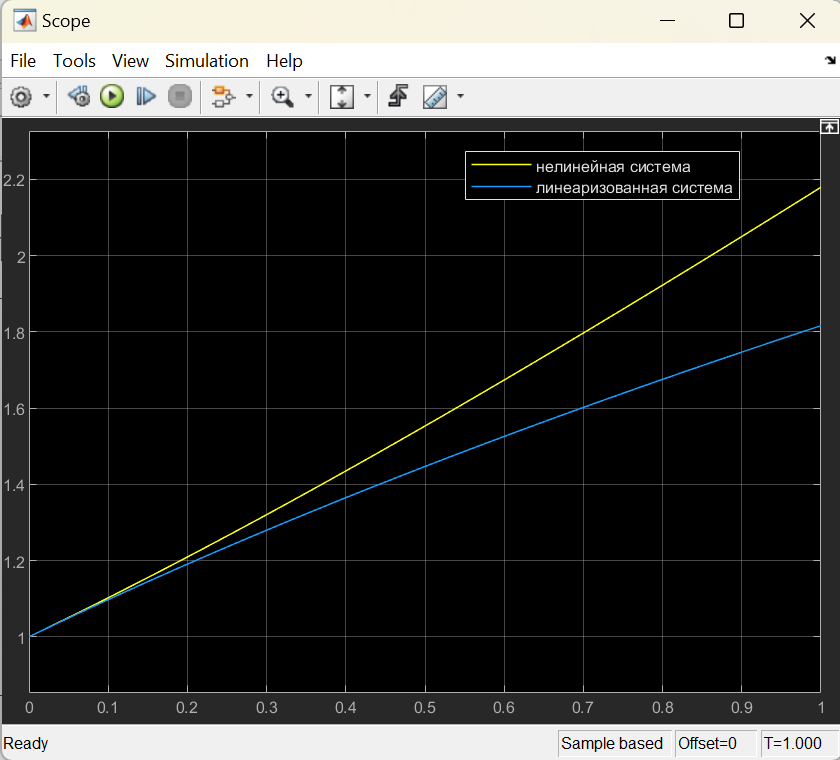 Рисунок 5 – График переходных процессов 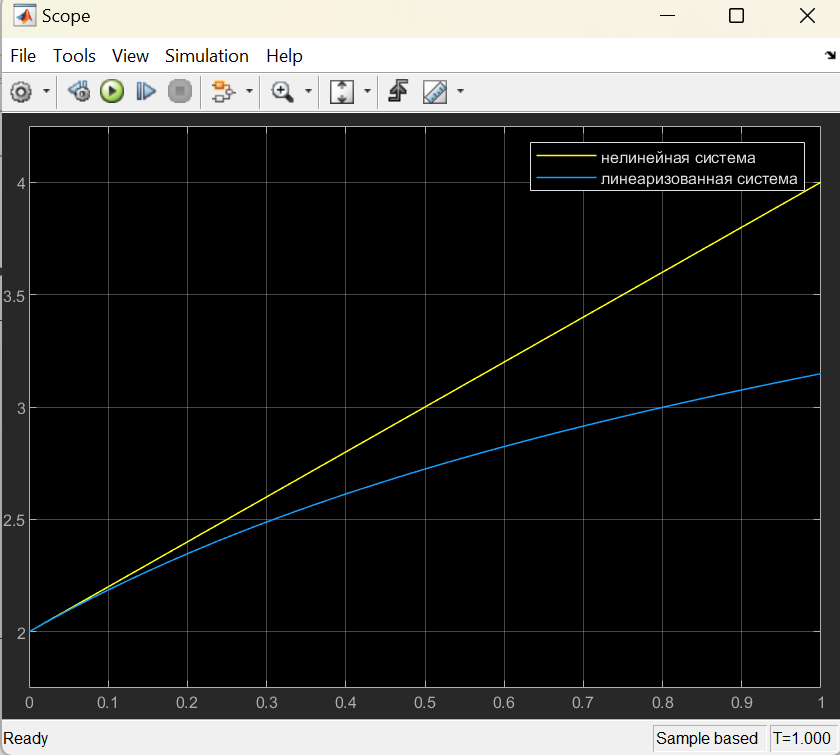 Рисунок 6 – График переходных процессов Вывод В ходе данной практической работы были получены навыки в выполнении линеаризации в пространстве состояний для нелинейных функций и проверки результатов моделированием в MatLab Simulink. |
