Передаточная функция исходной части системы
 Скачать 290.53 Kb.
|
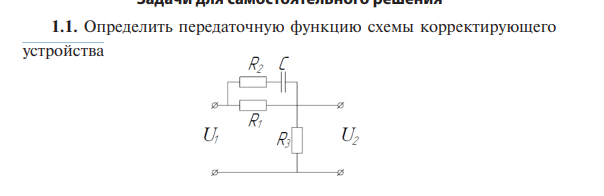 Передаточная функция исходной части системы , (7.0)где  ; ; ; передаточные функции приемника, фазового детектора, усилителя мощности и антенны с двигателем и редуктором.Параметры устройств исходной части системы: kп = 0,035 В/рад; kфд=0,8; kум = 10; k = 143 рад/(с В); Tп = Tфд = Tп=0,01 с; Tм = =0.02 с. Коэффициент передачи исходной части системы  . (7.0)С учетом требований к системе и формул (7.9)–(7.12) = 0,785 рад; ср = 7 с–1; С0 = 0; С1 = 0,01 с; С2 = 0,05 с2; К =100 с–1. В качестве желаемой передаточной функции разомкнутой системы примем функцию (7.7). Все частоты сопряжения передаточных функций устройств исходной части системы автоматического сопровождения (7.37) больше требуемой частоты среза, поэтому для упрощения корректирующих устройств включим передаточную функцию исходной части системы в состав желаемой передаточной функции. В результате получим 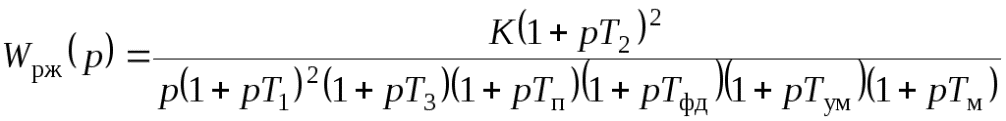 .(7.0)Постоянные времени T1, T2 и Т3 вычислим по формулам (7.19) и (7.20). Тогда T1 = 1,7 с; T2 = 0,45 с; T3 = 0,015 с. Так как значение T3 незначительно отличается от постоянной времени двигателя Tм=0,02 с, то для упрощения корректирующего устройства примем Т3=Тм. Передаточную функцию последовательного корректирующего устройства найдем, используя выражение (7.22):  , (7.0)где kкз = К/Ки–коэффициент передачи корректирующего звена; Ки – коэффициент передачи исходной части системы. Первый сомножитель в (7.40) реализуем в виде последовательного корректирующего устройства, включенного после фазового детектора, а второй – через эквивалентную обратную связь, передаточную функцию которой рассчитаем по формуле (7.24). Таким образом,  , (7.0)где k0 = (T1–T2)/(kykA) – коэффициент передачи цепи обратной связи. В выражении (7.41) пренебрегли постоянными времени Tу и Тм, так как соответствующие им частоты сопряжения намного больше частоты среза. Обратная связь с передаточной функцией (7.41) реализуется с помощью тахогенератора и дифференцирующей RC-цепи (рис. 7.6, б) с постоянной времени, равной T2. Передаточная функция цепи такой обратной связи имеет вид  , (7.0)где kтг – коэффициент передачи тахогенератора; kуо = k0/(k T2) – коэффициент усиления усилителя в цепи обратной связи. Так как при синтезе системы автоматического сопровождения были допущены упрощения, то необходимо проверить выполнение заданных требований. С этой целью на рис. 7.8 построены ЛЧХ спроектированной системы и ЛЧХ, соответствующие передаточной функции (7.39). 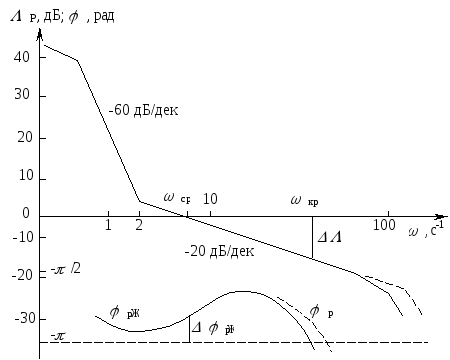 Рис. 1 ЛЧХ системы автосопровождения цели РЛС Из сравнений этих характеристик видно, что выполняются все заданные показатели качества работы системы автоматического сопровождения цели. 2.1 Для нижеприведенных схем определить передаточные функции систем по задающему и возмущающему воздействиям и определить установившиеся ошибки. 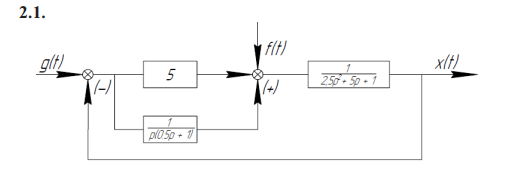 1. Статическая ошибка определяется следующим соотношением 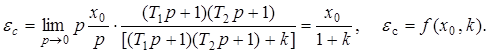 2. Кинетическая ошибка определяется следующим соотношением 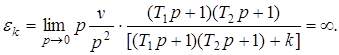 3. Инерционная ошибка определяется следующим соотношением 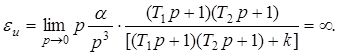 3.1. По передаточной функции построить логарифмические частотные характеристики  Приведем передаточную функцию (4.8) к виду (4.2). Для выполнения условия 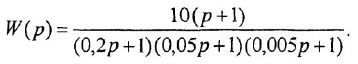 разделим числитель и знаменатель на 100, в результате чего полином второй степени, стоящий в знаменателе, принимает вид  , т. е. его свободный член становится равным единице. Нетрудно убедиться, что он разлагается на сомножители первой степени  . Тем самым передаточная функция преобразуется к требуемому виду: Сравнивая ее с выражениями (4.2)-(4.5), заключаем, что в данном случае  Определим частоты сопряжения ЛАХ. Их значения являются обратными по отношению к постоянным времени в выражениях для  и  : (частоты пронумерованы в порядке возрастания их значений). Нанесем соответствующие точки на ось абсцисс (для определения их положения вычисляем:  ) и проведем через них вертикальные пунктирные линии (рис. 4.2).Построение ЛАХ, согласно изложенной в 4.1 методике, начинаем с участка, представляющего собой ЛАХ пропорционального звена с передачей  . Это горизонтальная линия, имеющая ординату 20  10= 20 дБ. Ее проводим только до пунктирной линии, соответствующей первой сопрягающей частоте. Далее в ЛАХ должен произойти «излом». Поскольку частота  соответствует сомножителю  первой степени, стоящему в числителе, то «приращение наклона» второго участка ЛАХ по отношению к наклону первого участка составляет + 20 дБ/дек, поэтому второй участок проводим с коэффициентом наклона + 1 ( + 20 дБ^дек) — до следующей сопрягающей частоты . Эта частота соответствует сомножителю  первой степени, стоящему в знаменателе, поэтому наклон следующего, третьего, участка отличается от наклона предыдущего на -20 дБ/дек, т. е. его коэффициент наклона равен нулю. Совершенно аналогично на частотах  и  изменяем наклон участков ЛАХ на -20 дБ/дек, т. е. четвертый и пятый участки проводим с коэффициентами наклона, соответственно, -1 и -2.4.1. Определить устойчивость замкнутой системы, если дана передаточная функция разомкнутой систем  Для решения поставленной задачи воспользуемся критерием Гурвица. Найдем передаточные функции, а затем и характеристические уравнения разомкнутой и замкнутой систем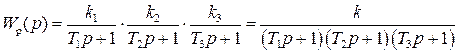. ,где 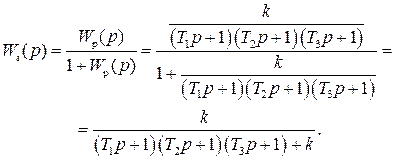 . Для разомкнутой системы характеристическое уравнение имеет вид  (IV. 3. 11) ,а для замкнутой САР получается  (IV. 3. 12) . (IV. 3.13)Нетрудно понять, что для исследования устойчивости разомкнутой САР применять критерий устойчивости Гурвица излишне, ибо непосредственно из вида характеристического уравнения разомкнутой системы (IV. 3. 11) легко найти, что все корни левые 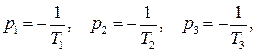 т. е. разомкнутая САР при всегда положительных Т1, Т2, Т3 устойчива. Вот по виду характеристического уравнения замкнутой САР (IV. 3. 12) так просто, как в предыдущем случае, определить соответствующие корни не удается, поэтому приходится применить критерий устойчивости Гурвица . При введении обозначений 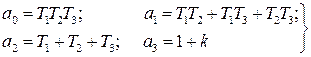 (IV.3. 14)характеристическое уравнение замкнутой САР (IV. 3. 13) примет вид  .В разделе IV. 2. 2 было выяснено, что для САР с характеристическим уравнением третьего порядка для устойчивости необходимо и достаточно при положительных коэффициентах ai( i =0, 1, 2,3) выполнение условия ( IV. 2. 3)  .Реклама Из видно, условия ai>0 при положительных Т1, Т2, Т3 и k всегда выполняются, а для проверки условия (IV. 2.3) надо в него подставить заданные значения параметров Т1, Т2, Т3 и k и определить знак минора   .Если этот минор больше нуля, то заданная замкнутая САР устойчива. Граничный коэффициент усиления kгр найдется из предпоследнего минора, приравненного к нулю 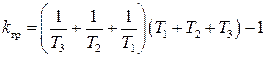 =0. . .Согласно условию Стодолы (что в данном случае совпадает с критерием Гурвица) САР не сожжет быть устойчивой, а только либо нейтральной либо неустойчивой. 5.1. Какую передаточную функцию должно иметь корректирующее звено (к.з.), чтобы ЛАХ разомкнутой системы (а) имела вид (б) 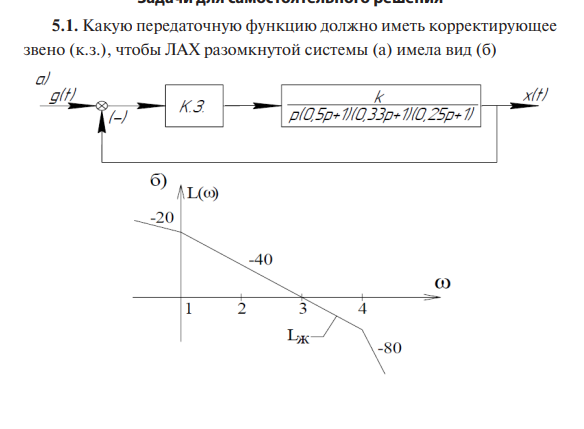 По виду ЛАХ корректирующего звена можно определить его передаточную функцию, как :Кк=10(-Lк/20)=0,12 На частоте происходит излом характеристики на +20 Дб/дек, что соответствует форсирующему звену с постоянной времени [1]: T1=1/  =0.02 Вторичный излом характеристики на +20 Дб/дек, происходит на частоте, что соответствует второму форсирующему звену с постоянной времени [1] : T2=1/  =0.017 На частоте происходит излом характеристики на – 40 Дб/дек, что может быть достигнуто включением двойного апериодического звена с постоянной времени [1]: T3=1/  =0.005 В результате перечисленных соображений получаем передаточную функцию корректирующего звена в следующем виде : Wk(p)=Kk  Для реализации полученной функции в качестве корректирующего звена был выбран четырехполюсник |