ТЭЦ Лабораторная работа №6. Исследование резонанса тока в простых электрических цепях
 Скачать 241.54 Kb. Скачать 241.54 Kb.
|
 ФАКУЛЬТЕТ «КОМПЬЮТЕРНЫХ ТЕХНОЛОГИЙ И КИБЕРБЕЗОПАСНОСТИ» КАФЕДРА «РАДИОТЕХНИКА, ЭЛЕКТРОНИКА И ТЕЛЕКОММУНИКАЦИИ» Лабораторная работа №6 Тема: ИССЛЕДОВАНИЕ РЕЗОНАНСА ТОКА В ПРОСТЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ По дисциплине «Теория электрических цепей» Выполнила: студентка группы ССТ-2002, Амантай Айғаным Проверила: ассоциированный профессор – АО МУИТ, Иманбекова Тохтабуби Джумадиловна Алматы 2021 ЛАБОРАТОРНАЯ РАБОТА № 6. ИССЛЕДОВАНИЕ РЕЗОНАНСА ТОКА В ПРОСТЫХ ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ Цель работы: исследование основных параметров и амплитудно-частотных характеристик параллельного колебательного контура. Общие сведения Параллельным колебательным контуром называется параллельное соединение индуктивного и емкостного элемента. В параллельном колебательном контуре наблюдается резонанс токов. Эквивалентная схема параллельного колебательного контура изображена на рисунке 1. 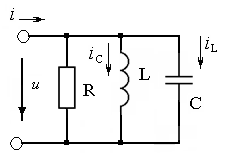 Рисунок 1. Схема параллельного колебательного контура Комплексная проводимость всей цепи 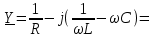 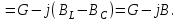 Резонанс токов представляет такой режим цепи, при котором реактивная проводимость всей цепи равна нулю Резонанс токов представляет такой режим цепи, при котором реактивная проводимость всей цепи равна нулю 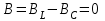 . Отсюда следует, равенство индуктивной проводимости ветви с катушкой . Отсюда следует, равенство индуктивной проводимости ветви с катушкой 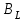 и емкостной проводимости ветви с конденсатором и емкостной проводимости ветви с конденсатором 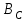 . Характеристическая проводимость . Характеристическая проводимость 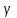 равна индуктивной или емкостной проводимости при резонансной частоте равна индуктивной или емкостной проводимости при резонансной частоте 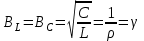 . Резонансная частота контура . Резонансная частота контура 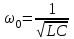 или или 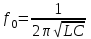 . Угол сдвига фаз между напряжением и током цепи равен нулю и цепь потребляет только активную мощность. . Угол сдвига фаз между напряжением и током цепи равен нулю и цепь потребляет только активную мощность. При резонансе токов полная проводимость параллельного колебательного контура минимальна, входное сопротивление достигает максимума. При этом ток источника минимален и равен 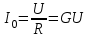 . Токи в индуктивном и емкостном элементах компенсируют друг друга . Токи в индуктивном и емкостном элементах компенсируют друг друга 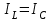 и могут быть во много раз больше тока источника. и могут быть во много раз больше тока источника. Отношение действующего значения тока любого из реактивных элементов к току источника при 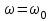 называют добротностью параллельного контура: называют добротностью параллельного контура: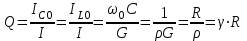 , т. е. обратно по величине добротности последовательного контура. , т. е. обратно по величине добротности последовательного контура. По измеренным в режиме резонанса значениям входного тока 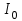 , тока в емкостном элементе , тока в емкостном элементе 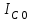 , напряжения на входе , напряжения на входе 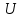 , резонансной частоты , резонансной частоты 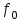 можно определить параметры контура: активную проводимость или активное сопротивление цепи можно определить параметры контура: активную проводимость или активное сопротивление цепи 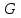 ( (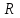 ), добротность и затухание контура ), добротность и затухание контура 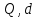 , характеристическую проводимость , характеристическую проводимость 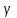 или характеристическое сопротивление или характеристическое сопротивление 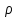 , а также емкость и индуктивность элементов , а также емкость и индуктивность элементов 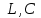 . Параметры контура определяются из соотношений: . Параметры контура определяются из соотношений: 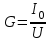 , , 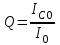 , , 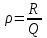 , , 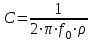 , , 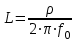 . .Комплексная передаточная функция по току в ветвях 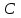 и и 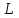 параллельного колебательного контура: параллельного колебательного контура: 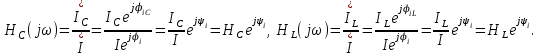 Амплитудно-частотная характеристика комплексной передаточной функции по току: Амплитудно-частотная характеристика комплексной передаточной функции по току: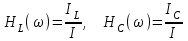 . .  Зависимость характеристик параллельного контура от частоты называются частотными характеристиками: 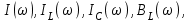 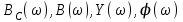 . .Экспериментальная часть Задание 1. Для цепи с параллельным соединением конденсатора и катушки индуктивности измеряем действующее значения напряжения 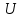 и токов и токов 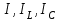 при частоте при частоте 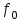 , , 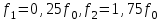 . . 1. Приводим компьютер в рабочее положение и открываем программу ELECTRONICS WORCBENCH (EWB). Согласно варианту задания (Таблица №1), собираем схему электрической цепи, изображенной на рисунке 2. Подсоединяем регулируемый источник синусоидального напряжения и устанавливаем его напряжение 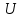 . .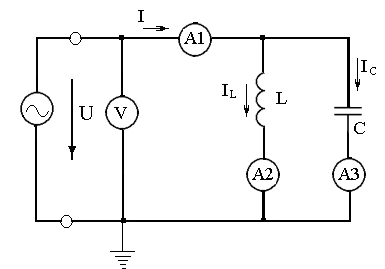 Рисунок 2. 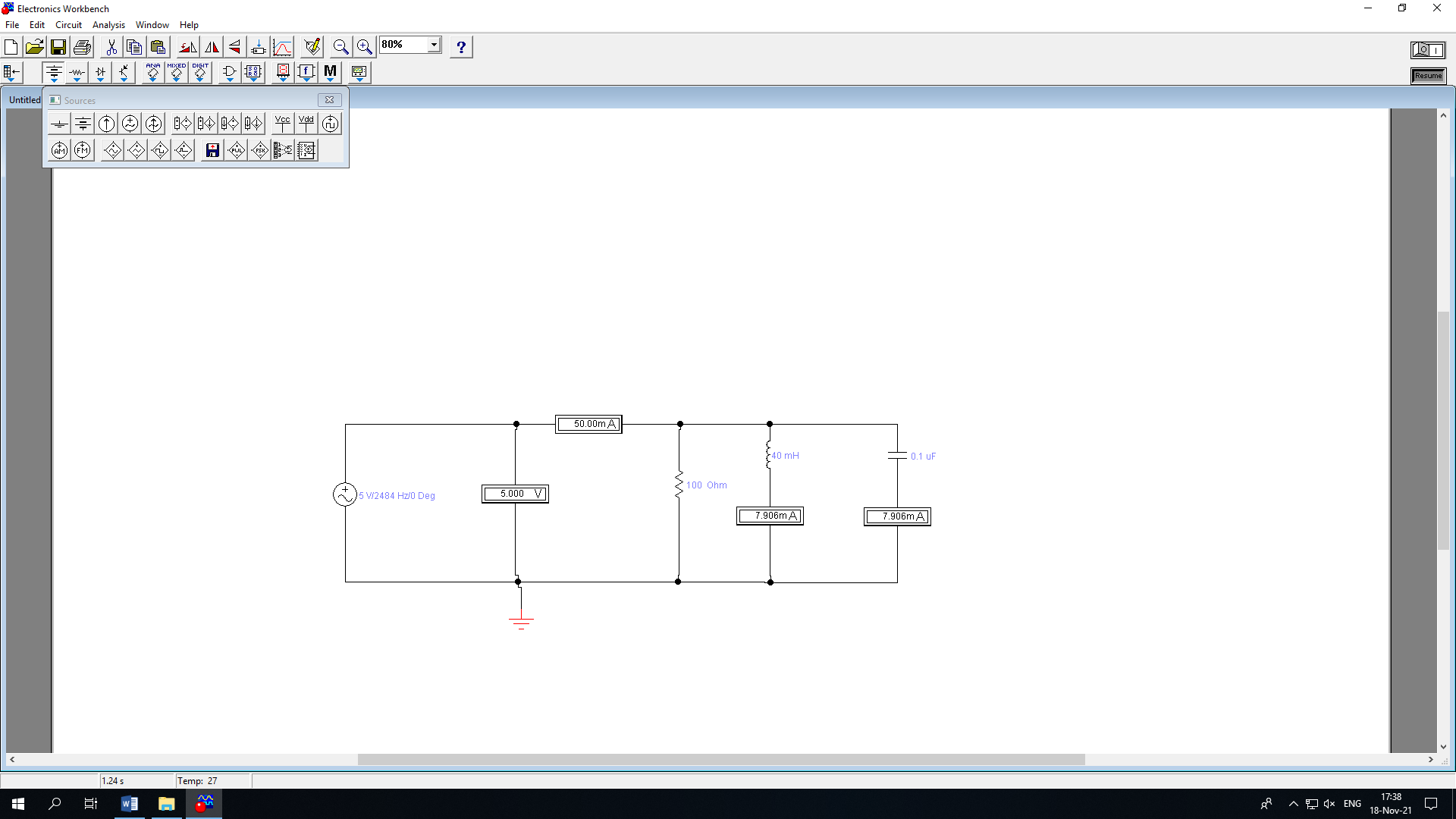 2. Исходя из выбранных параметров, рассчитываем теоретическую резонансную частоту параллельного колебательного контура 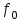 . . f0= 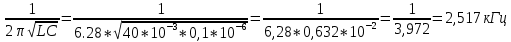 3. Изменяя частоту приложенного напряжения, определяем экспериментальную резонансную частоту параллельного контура по показаниям амперметров. При резонансе токи 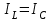 , а ток , а ток 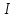 минимальный. Сравниваем экспериментальную и расчетную резонансную частоту. минимальный. Сравниваем экспериментальную и расчетную резонансную частоту.Варианты задания Таблица №1
4 При частоте 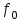 снимаем показания всех приборов. Результаты всех измерений заносим в Таблицу №2. снимаем показания всех приборов. Результаты всех измерений заносим в Таблицу №2.Таблица №2
Частоты источника: 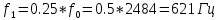 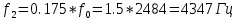 По данным измерений вычисляем фактические параметры контура: проводимость потерь, добротность, характеристическое сопротивление, затухание контура, а также емкость и индуктивность элементов: 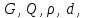 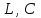 . Результаты расчетов заносим в Таблицу №2. . Результаты расчетов заносим в Таблицу №2.Добротность контура: IL = IC 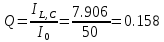 Волновое сопротивление контура: 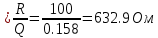 Затухание контура: 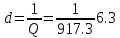 Фактическое значение индуктивности катушки: 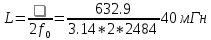 Фактическое значение емкости конденсатора: 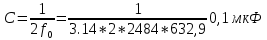 Максимальное значение тока в цепи (теоретически): 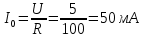 Задание 2. Исследование амплитудно-частотных характеристик контура с малыми потерями. 1. Снимаем экспериментально частотные характеристики параллельного резонансного контура. Для этого, изменяя частоту источника питания в пределах 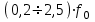 и поддерживая постоянным действующее значение напряжения источника и поддерживая постоянным действующее значение напряжения источника 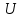 , измеряем ток во входной ветви , измеряем ток во входной ветви 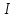 , токи в параллельных ветвях , токи в параллельных ветвях 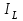 и и 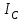 , , 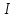 . Результаты измерений заносим в Таблицу №3. . Результаты измерений заносим в Таблицу №3.Таблица №3
Вычисление значений: Индуктивная проводимость 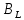 : :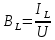 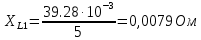 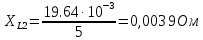 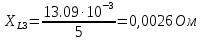 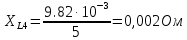 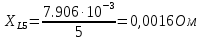 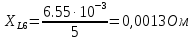 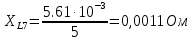 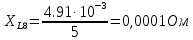 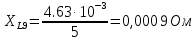 Емкостная проводимость 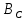 : :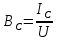 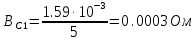 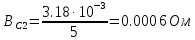 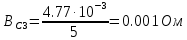 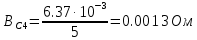 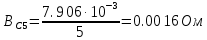 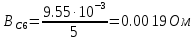 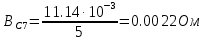 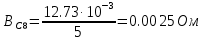 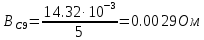 Проводимость 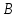 : :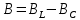 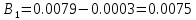 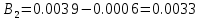 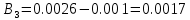 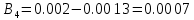 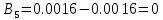 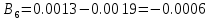 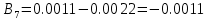 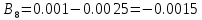 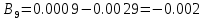 Угловая частота  : :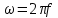 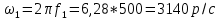 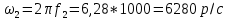 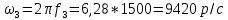 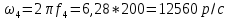 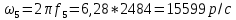 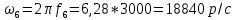 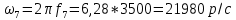 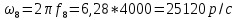 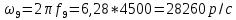 2. По результатам измерений вычисляем значения 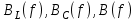 и заносим в Таблицу №3. Строим частотные характеристики и заносим в Таблицу №3. Строим частотные характеристики 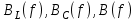 . Кривые изменения . Кривые изменения 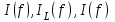 строим на отдельном графике. Даем объяснения соответствующим кривым. строим на отдельном графике. Даем объяснения соответствующим кривым.Используя эквивалентные схемы цепи для 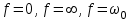 определяем значения АЧХ на этих частотах и контролируем результаты эксперимента. определяем значения АЧХ на этих частотах и контролируем результаты эксперимента.3. Выводы по работе: | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

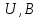
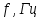
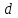
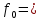 2484
2484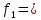 621
621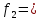 4347
4347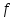 ,
, 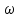 ,
,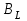 ,
, 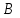 ,
,