лабораторная 2 физика. Laboratornaya_1 макжанов. Исследование соударения шарика со стенкой фио студента
 Скачать 497.05 Kb. Скачать 497.05 Kb.
|
|
Лабораторная работа 1 по дисциплине «Физика» по теме: Исследование соударения шарика со стенкой
ОглавлениеЦель работы: 3 Оборудование: 3 Теоретическое обоснование: 3 Ход работы 4 Часть 1. Определение коэффициента восстановления E. 4 Часть 2. Определение продолжительности удара t, средней силы взаимодействия шарика со стенкой F и скорости шарика в начале удара V. 7 Часть 3. Расчёт погрешностей, расчёт значений с учётом погрешностей, построить график 10 Вывод. 10 Цель работы: Определение коэффициента восстановления, продолжительности удара и средней силы взаимодействия шарика со стенкой. Оборудование: Кронштейн, к которому на двух тонких проволоках подвешен шарик и прикреплён железный рельс, по которому может ездить каретка, закрепляющая положение шарика в состоянии отклонения на определённый угол. К кронштейну присоединена электрическая схема, состоящая из резистора, последовательно подключённого к системе параллельно подключённых ЭДС, конденсатора, вольтметра, последовательно подключённой к шарику, который при соприкосновении с кронштейном замыкает цепь. Длина нити l = 10 см Масса шарика m = 23 г Сопротивление R = 220 Ом Ёмкость C = 2 мкФ Теоретическое обоснование: В предельном случае абсолютно упругого удара кинетическая энергия системы, состоящей из шарика и стенки, сохраняется. Как следствие, выполняется соотношение: Коэффициент восстановления E = 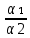 при малых α₁ и α₂ при малых α₁ и α₂Скорость в начале удара V = 2 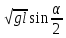 , м/с , м/сПродолжительность удара t = RC ln 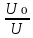 , с , сСила удара F = 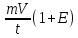 , Н , Н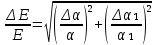 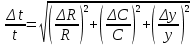 , где y = , где y = 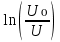 , , 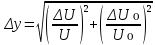 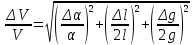 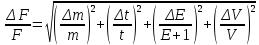 Ход работы Часть 1. Определение коэффициента восстановления E. Отклоняем шарик на угол 15°, отпускаем и замеряем α₁. Повторяем 4 раза. Заносим результат в таблицу. Считаем коэффициент восстановления E. 
Eср = 0,47 Отклоняем шарик на угол 10°, отпускаем и замеряем α₁. Повторяем 4 раза. Заносим результат в таблицу. Считаем коэффициент восстановления E. 
Eср = 0,5 Отклоняем шарик на угол 5°, отпускаем и замеряем α₁. Повторяем 4 раза. Заносим результат в таблицу. Считаем коэффициент восстановления E. 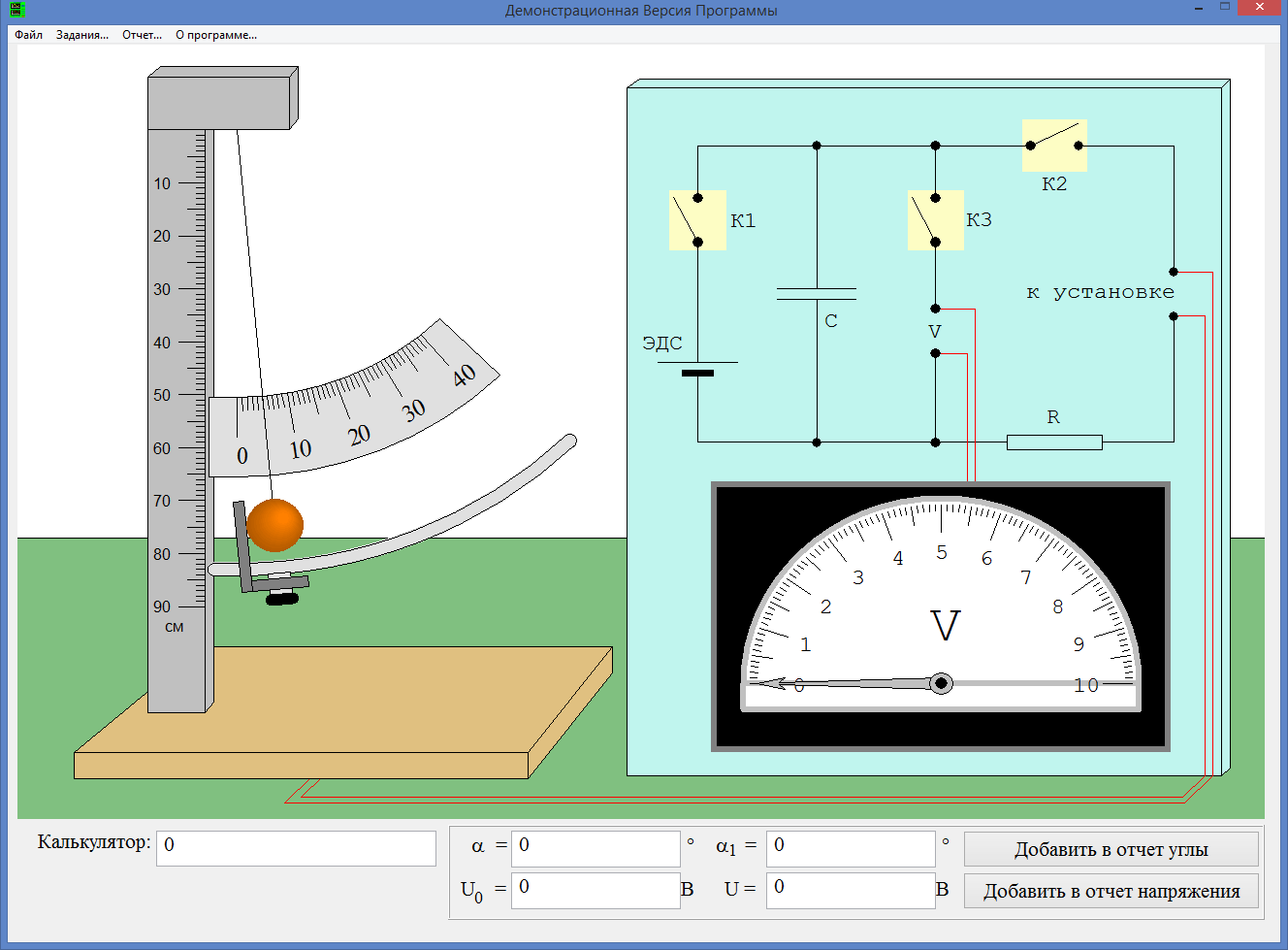
Eср = 0,7 Часть 2. Определение продолжительности удара t, средней силы взаимодействия шарика со стенкой F и скорости шарика в начале удара V. Отводим шарик на 15°. Подключаем конденсатор к источнику ЭДС. Замеряем напряжение на конденсаторе и заносим его в таблицу. Отключаем конденсатор от источника ЭДС и подключаем его к цепи, связанной с нитью и шариком. Отпускаем шарик. Замеряем напряжение на конденсаторе после соударения и заносим в таблицу. Вычисляем продолжительность удара t, среднюю силу взаимодействия шарика со стенкой F и скорость шарика в начале удара V. 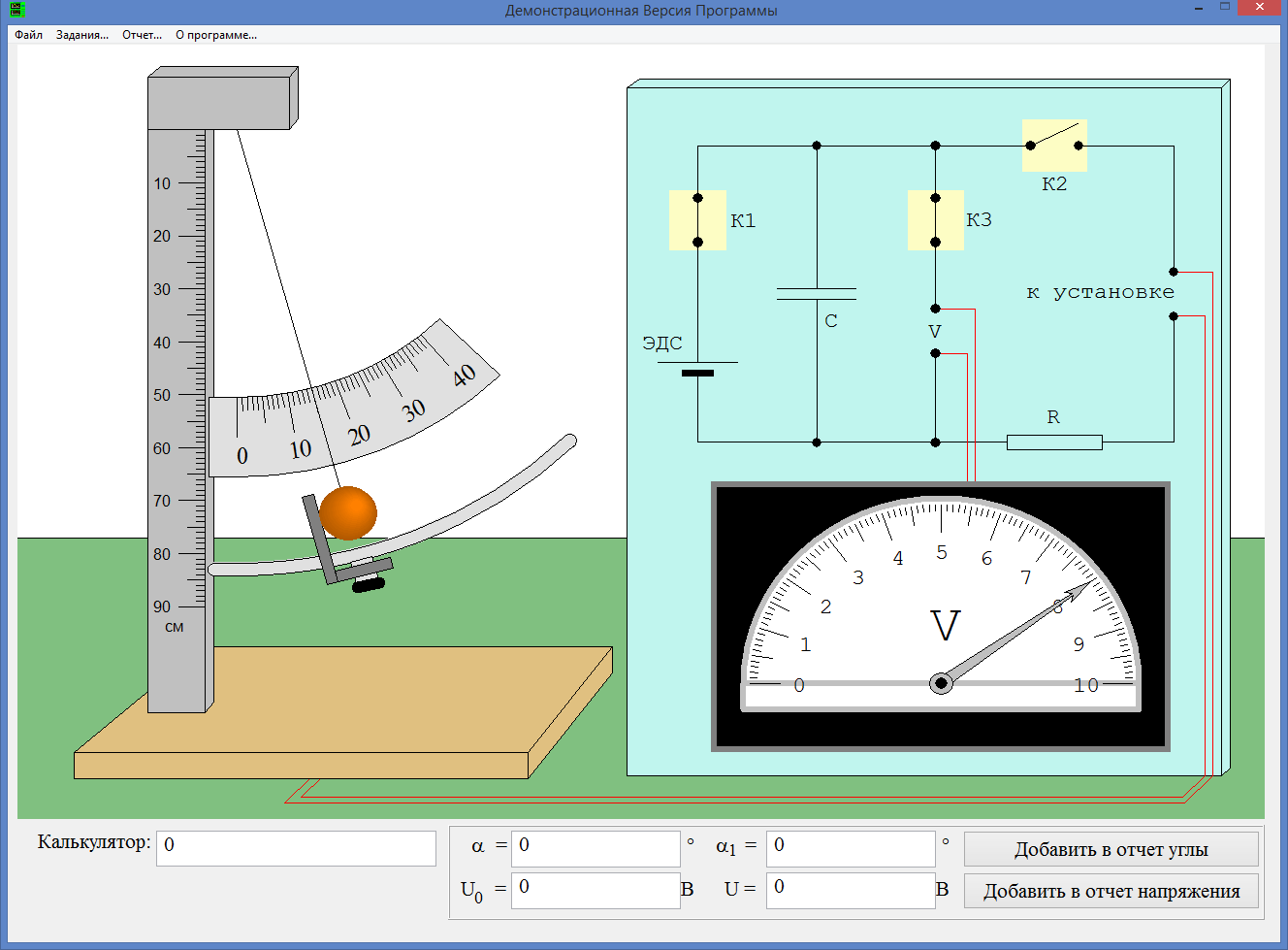
Отводим шарик на 10°. Подключаем конденсатор к источнику ЭДС. Замеряем напряжение на конденсаторе и заносим его в таблицу. Отключаем конденсатор от источника ЭДС и подключаем его к цепи, связанной с нитью и шариком. Отпускаем шарик. Замеряем напряжение на конденсаторе после соударения и заносим в таблицу. Вычисляем продолжительность удара t, среднюю силу взаимодействия шарика со стенкой F и скорость шарика в начале удара V. 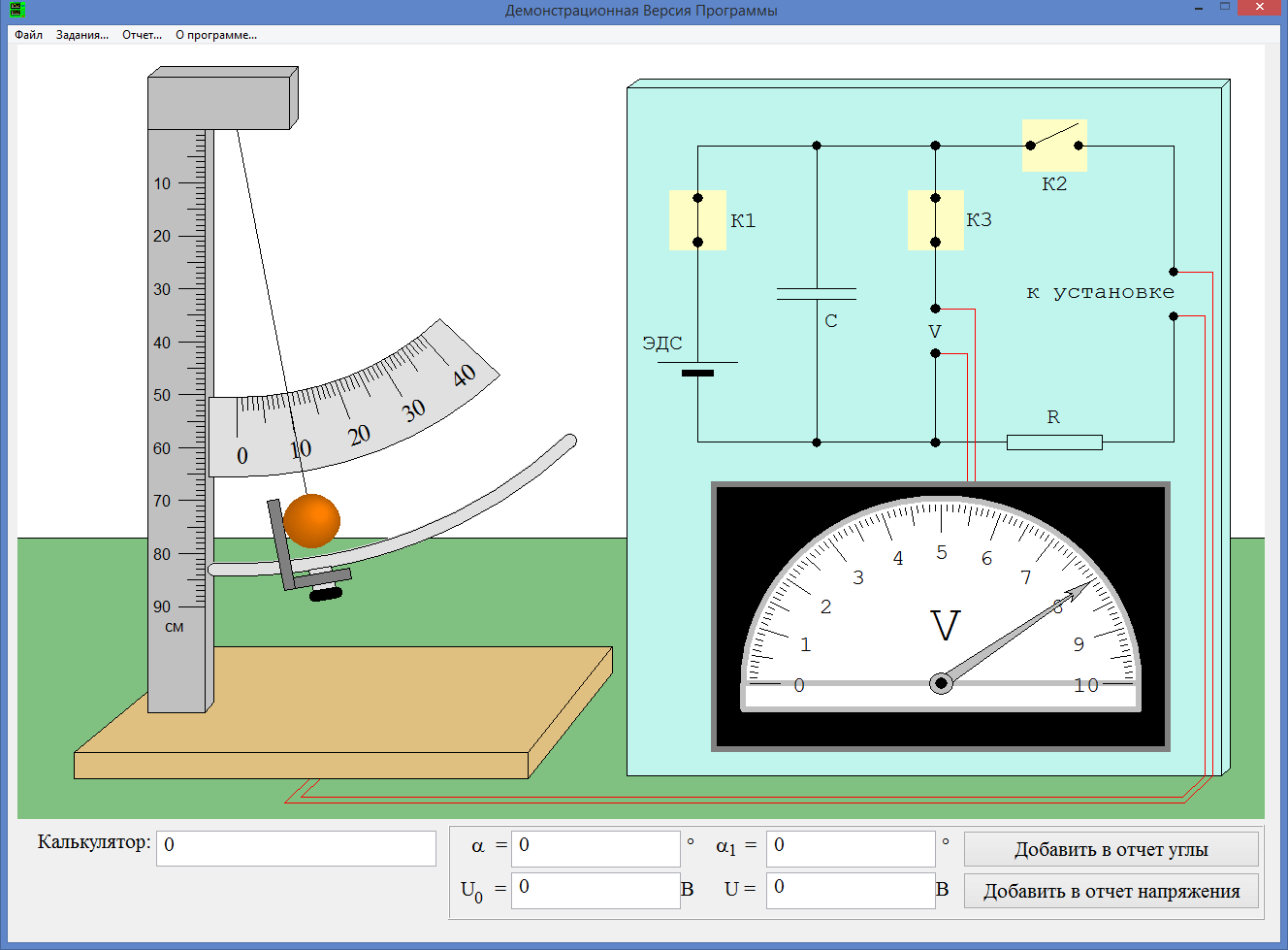
Отводим шарик на 5°. Подключаем конденсатор к источнику ЭДС. Замеряем напряжение на конденсаторе и заносим его в таблицу. Отключаем конденсатор от источника ЭДС и подключаем его к цепи, связанной с нитью и шариком. Отпускаем шарик. Замеряем напряжение на конденсаторе после соударения и заносим в таблицу. Вычисляем продолжительность удара t, среднюю силу взаимодействия шарика со стенкой F и скорость шарика в начале удара V. 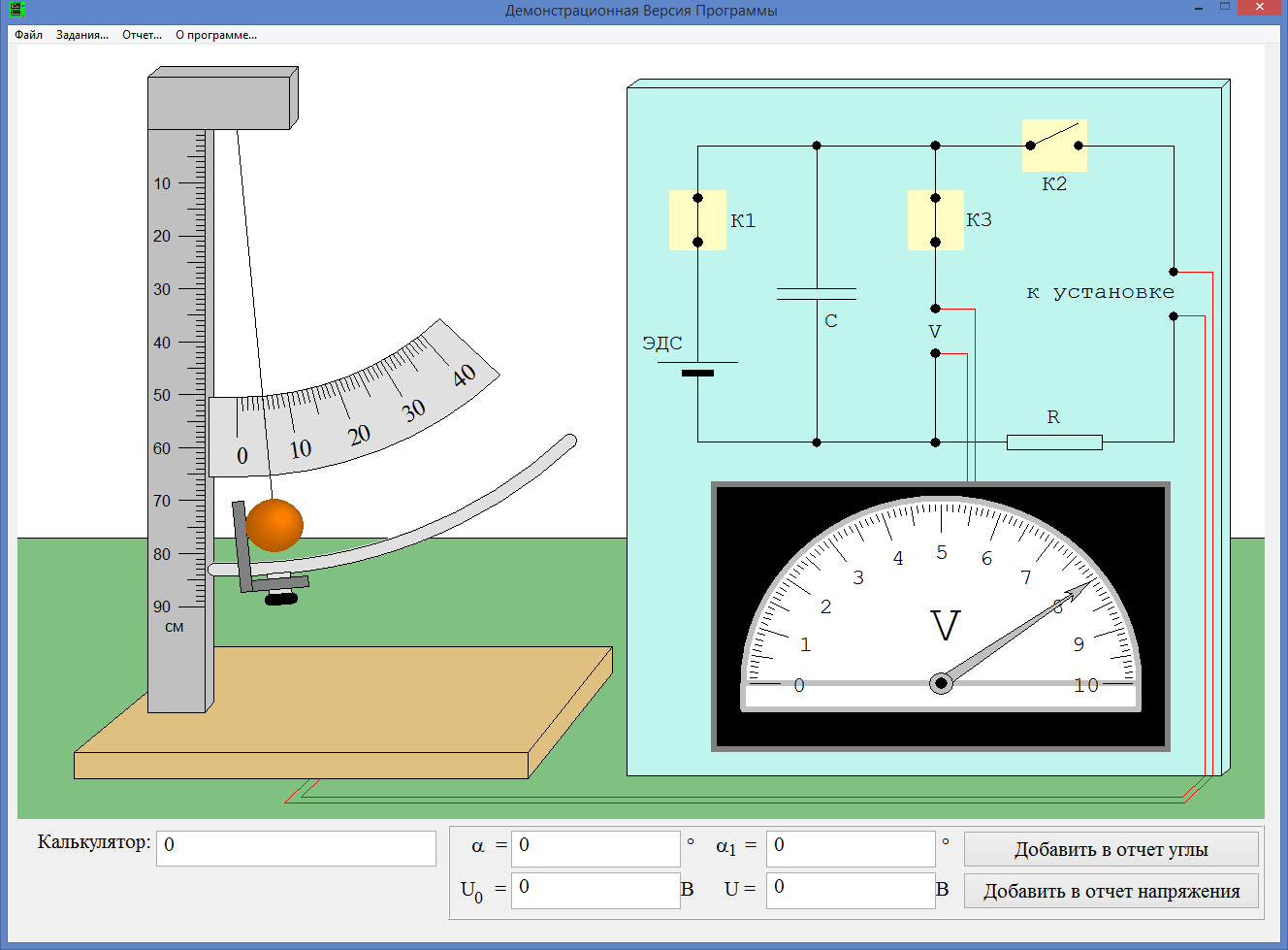
Часть 3. Расчёт погрешностей, расчёт значений с учётом погрешностей, построить график
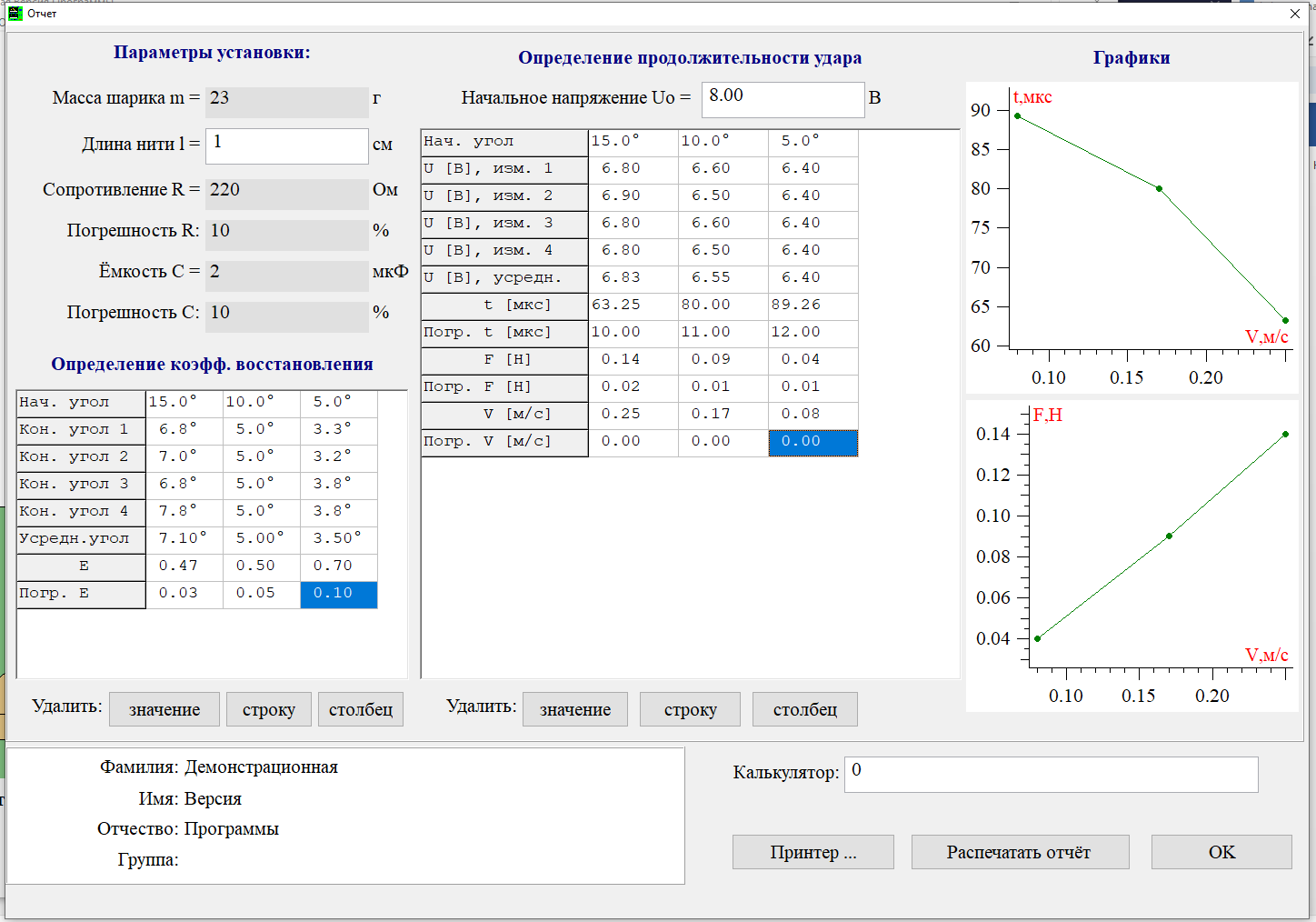 Вывод. Зависимость времени удара t от скорости в начале удара V близка к линейной, обратно пропорциональной зависимости, а зависимость силы удара F от скорости в начале удара V близка к линейной, пропорциональной зависимости. |
