Исследование стержневого пьезокерамического элемента методом резонанса-антирезонанса. Исследование стержневого пьезокерамического элемента методом резонансаантирезонанса
 Скачать 216.24 Kb. Скачать 216.24 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ Федеральное государственное автономное образовательное учреждение высшего образования «ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕСИТЕТ» Институт нанотехнологий, электроники и приборостроения Кафедра электрогидроакустической и медицинской техники Дисциплина «Преобразователи физических величин» ОТЧЁТ о выполнении лабораторной работы № 2 «Исследование стержневого пьезокерамического элемента методом резонанса-антирезонанса» Выполнил: Студент группы ЭПбо 3-3 Ибрагимов А.А. Проверил: Преподаватель кафедры ЭГА и МТ Вареникова А. Ю. Дата выполнения: 24.11.2021 Таганрог 2021 Цель работы Освоение методики измерения параметров пьезокерамики (ГОСТ 12370-81) и пьезоэлементов; изучение стержневого элемента как системы с распределенными параметрами; оценка его эквивалентной схемы вблизи резонанса как системы с сосредоточенными параметрами; освоение методик расчета АЧХ и обработки результатов измерений; освоение способа управления спектральными составляющими и эффективностью. Основные теоретические сведения Математической моделью, используемой в методе, служат выражения для общей проводимости или импеданса, рассчитанные по формуле (1), полученные из решения электромеханической задачи об одномерных колебаниях ПКЭ: 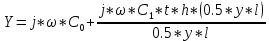 (1) (1)где 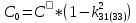 ; ;  ; γ=α+jβ – постоянная распространения ; γ=α+jβ – постоянная распространения 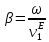 – волновое число; – волновое число; 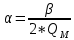 – коэффициент потерь; QM – механическая добротность; z – резонансный размер (l - для стержня, t - для пластины). – коэффициент потерь; QM – механическая добротность; z – резонансный размер (l - для стержня, t - для пластины).Поскольку th(γl/2) - функция нечетная, в спектре будут присутствовать только нечетные гармоники. Экспериментальный метод основан на измерении частот fm и fn (максимума и минимума полной проводимости или импеданса), по которым рассчитываются упругие коэффициенты и коэффициент электромеханической связи (КЭМС). Дополнительные измерения емкости свободного образца позволяют оценить величину диэлектрической проницаемости и пьезоконстант. Основными недостатками метода являются: • замена частот последовательного fs и параллельного fr резонансов, для которых получены основные соотношения, на частоты максимума fm и минимума fn полной проводимости соответственно, так как в исходных формулах не учтены механические, пьезоэлектрические и диэлектрические потери; • диэлектрические параметры измеряются на низких, а не на рабочих частотах; • влияние конечных размеров на точность определения констант пьезоматериалов и пьезорезонаторов (ПКР). Основные достоинства: • простота и доступность математического и аппаратурного обеспечения; • высокая точность определения характеристических частот и рассчитываемых по ним упругих констант; • удовлетворительная точность измерений коэффициентов электромеханической связи и пьезоконстант при условии  (здесь (здесь 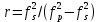 ; ; • возможность автоматизации метода измерений при необходимости оценки параметров большого количества ПКЭ или ПКР. Эквивалентная схема Стержень с нагрузкой на двух концах, в отличие от кольца, представляет собой систему с распределенными параметрами. Теоретически система с распределенными параметрами стержневого типа без учета потерь представляется эквивалентной схемой в виде длинной линии и при отсутствии нагрузки {F1=F2=0) может быть приведена к двум сопротивлениям (рисунок 1):  Рисунок 1 – Эквивалентная схема На эквивалентной схеме z0 =ρυS - характеристический импеданс, где скорость звука υ определяется выбранной модой колебаний; S - поперечное сечение; ρ - удельная плотность материала; F1, F2 - силы, действующие на концах стержня (могут быть заменены на сопротивления нагрузки z1 и z2); n - коэффициент электромеханической трансформации; Zс - комплексное емкостное сопротивление пьезоэлемента. Поскольку на резонансе аргумент 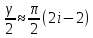 , где i= 1, 2, 3 …, необходимо эквивалентную схему представить в сосредоточенных параметрах. Так как гармоники разнесены далеко, на каждом резонансе будет действовать соответствующая эквивалентная схема (рисунок 2). При отсутствии нагрузки (F=0) электроды на механической стороне закарачиваются. , где i= 1, 2, 3 …, необходимо эквивалентную схему представить в сосредоточенных параметрах. Так как гармоники разнесены далеко, на каждом резонансе будет действовать соответствующая эквивалентная схема (рисунок 2). При отсутствии нагрузки (F=0) электроды на механической стороне закарачиваются. Рисунок 2 – Эквивалентная схема в сосредоточенных параметрах Механическое сопротивление пересчитывается на электрическую сторону и рассчитывается по формуле (2): 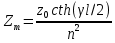 (2) (2)При разделении электродов эквивалентная схема приобретает для каждой гармоники вид, показанный на рисунке 3. Коммутируя электроды соответствующим образом, можно изменить спектр частот. При этом энергия перекачивается на определенные частоты. Это связано с тем, что электроды являются эквипотенциальными поверхностями, вытянутыми вдоль направления колебаний (при мягкой моде, т.е. поперечном пьезоэффекте). Заряды, возникающие за счет пьезоэффекта, зависят от механического напряжения, возникающего в пьезоэлементе на резонансе при приложенном напряжении  ,где х изменяется от (-l/2) до (+l/2), Распределение механического напряжения вдоль длины стержня показано на рисунке 3. Коммутируя электроды, можно складывать или вычитать возникающие заряды, перекачивая энергию с одних гармоник на другие . В случае продольного пьезоэффекта аналогичный результат можно получить для составных стержней. ,где х изменяется от (-l/2) до (+l/2), Распределение механического напряжения вдоль длины стержня показано на рисунке 3. Коммутируя электроды, можно складывать или вычитать возникающие заряды, перекачивая энергию с одних гармоник на другие . В случае продольного пьезоэффекта аналогичный результат можно получить для составных стержней.Аналогичное разделение электродов можно выполнить на диске по узловым линиям в соответствии с распределением деформаций, показанных на рисунке 4, и исследовать изменение спектра.  Рисунок 3 - Собственные формы колебаний стержней: а - стержень со свободными концами; б - стержень с закрепленными концами 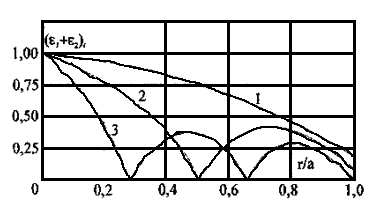 Рисунок 4 - Распределение деформаций в плоскости диска (i = 1, 2, 3) Описание установки Измерение динамических параметров пьезоэлемента методом резонананса-антирезонанса выполняется на установке, с помощью пассивного четырехполюсника, функциональная схема которого приведена на рисунке 5: 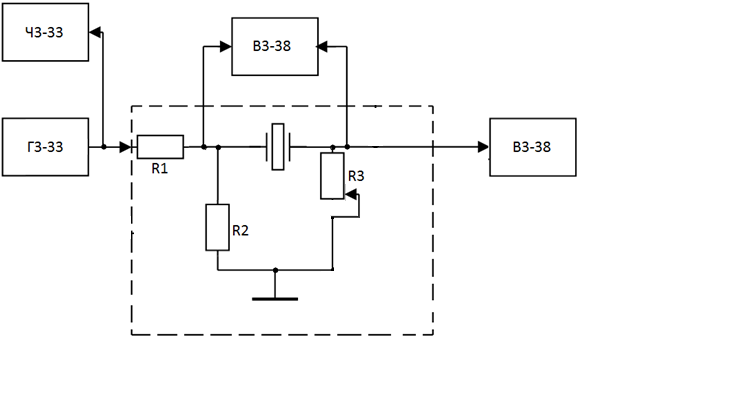 Рисунок 5 - Функциональная схема установки Делитель R1/R2 предназначен для стабилизации напряжения на пьезоэлементе при резком изменении Y(f). Сопротивление RЗ « RПЭ на резонансе, иначе оно будет влиять на величину Rn3. На антирезонансе сопротивление RПЭ велико, а токи малы, поэтому при измерениях сопротивление R3 увеличивают в 100 и 1000 раз для увеличения чувствительности. При этом условие RЗ « RПЭ должно выполнятся. В измерительной схеме может присутствовать фазометр (как при измерениях на кольце), тогда можно измерить значение Y(f) при φ=0 и рассчитать значения параметров для этих частот. Истинные значения параметров будут находиться в интервале между двумя измерениями. Характеристики пьезокерамики 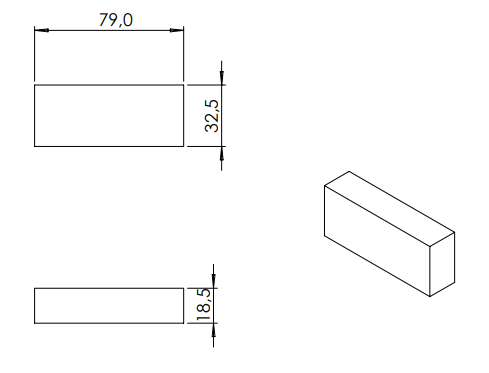 Рисунок 6 – Эскиз преобразователя Геометрические размеры и основные параметры пьезокерамики приведены в таблицах 1 и 2 соответственно: Таблица 1 – Геометрические размеры пьезокерамики
Таблица 2 – Основные параметры пьезокерамики
Результаты измерений Полученные, в ходе выполнения лабораторной работы, данные приведены в таблице 3: Таблица 3 – Результаты измерений
Результаты обработки данных в программной среде MathCAD: Графики АЧХ для А – первой, Б – второй и В – третьей резонансной частоты приведены на рисунке 7: 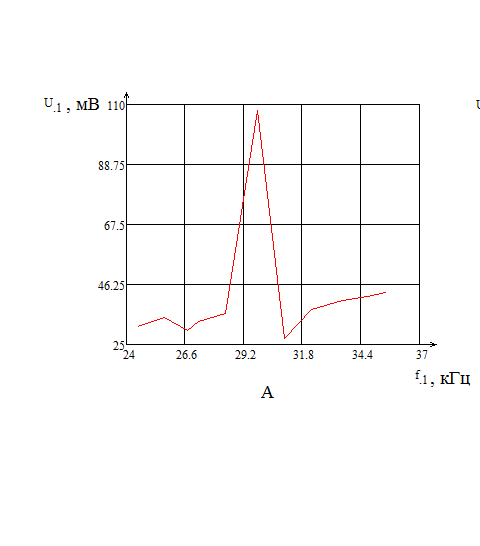 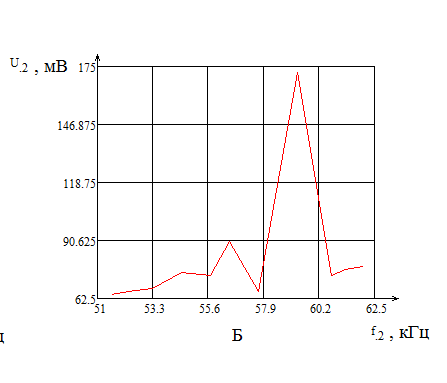 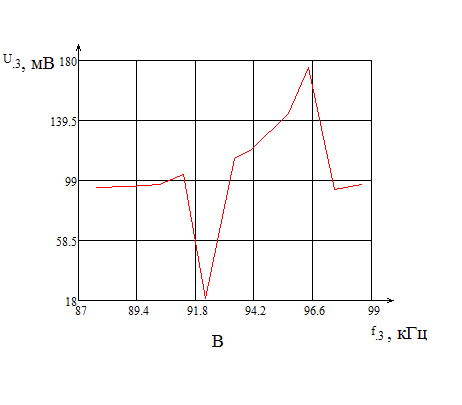 Рисунок 8 - Графики АЧХ для А – первой, Б – второй и В – третьей резонансной частоты Результаты предварительного расчета параметров пьезоэлемента в среде MathCAD:   Расчётные и измеренные параметры эквивалентной схемы элементов приведены в таблице 4. Таблица 4 – Расчетные и измеренные параметры
Вывод. В ходе лабораторной работы экспериментально были измерены частоты fm и fn (максимума и минимума полной проводимости или импеданса) с помощью изменения напряжения U3, зависимость которых приведена в таблице 3, по которым рассчитывались упругие коэффициенты и коэффициент электромеханической связи (КЭМС). Были найдены основные параметры для керамики марки ЦТС-19, приведенные в таблице 2, и измерены геометрические размеры пьезоэлемента, показанные в таблице 1. По полученным величинам частот f1,2,3 и напряжений U1,2,3 были построены амплитудно-частотные характеристики (АЧХ), приведенные на рисунке 8. Было проведено сравнение некоторых расчетных и измеренных параметров пьезоэлемента, которое показано в таблице 4. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
