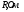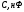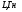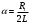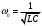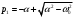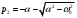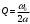Лаб 3_ Бутвинский_Никита_9106 (1) (1) (1) (1). Исследование свободных процессов в электрических цепях
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Теоритических основ электротехники (ТОЭ) отчет по лабораторной работе №3 по дисциплине «Теоретические основы электротехники» Тема: ИССЛЕДОВАНИЕ СВОБОДНЫХ ПРОЦЕССОВ В ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ
Санкт-Петербург 2021 Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности RLC -контура по осциллограммам. 3.2.1. Исследование свободного процесса в цепи первого порядка 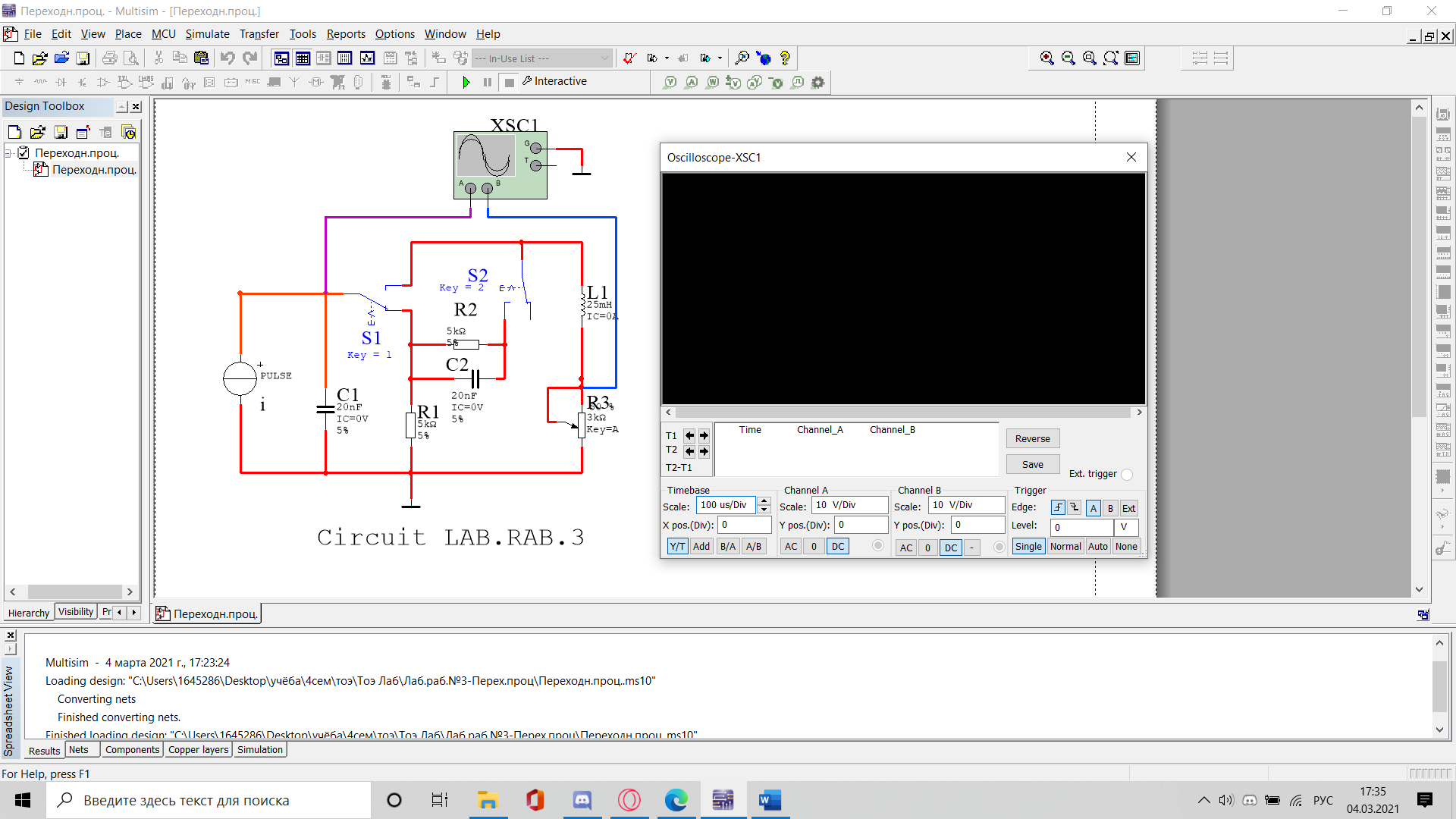 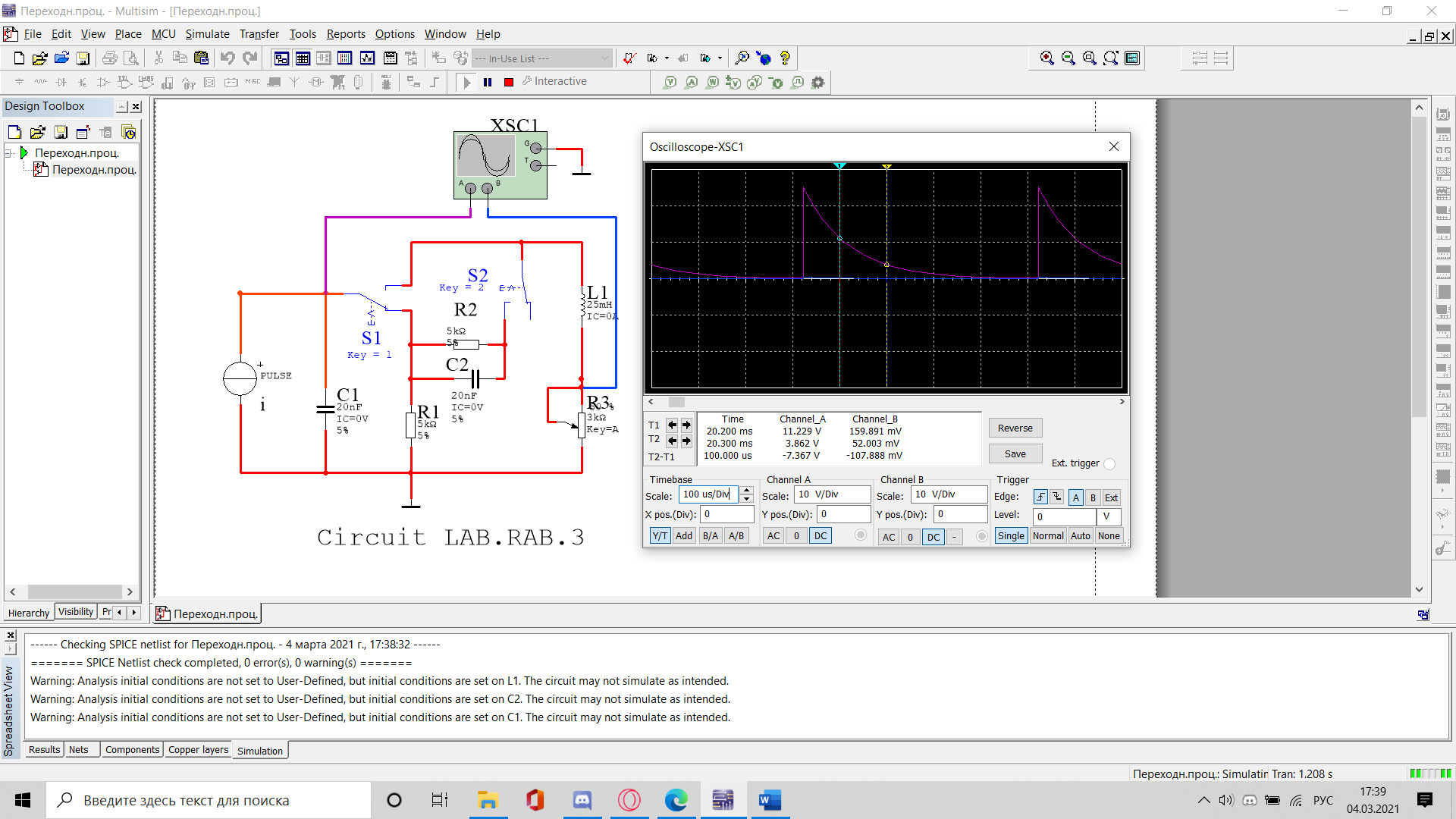 По формуле 3.6 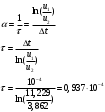 По формуле 3.1 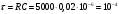 3.2.2. Исследование свободных процессов в цепи второго порядка Апериодический(R100%) 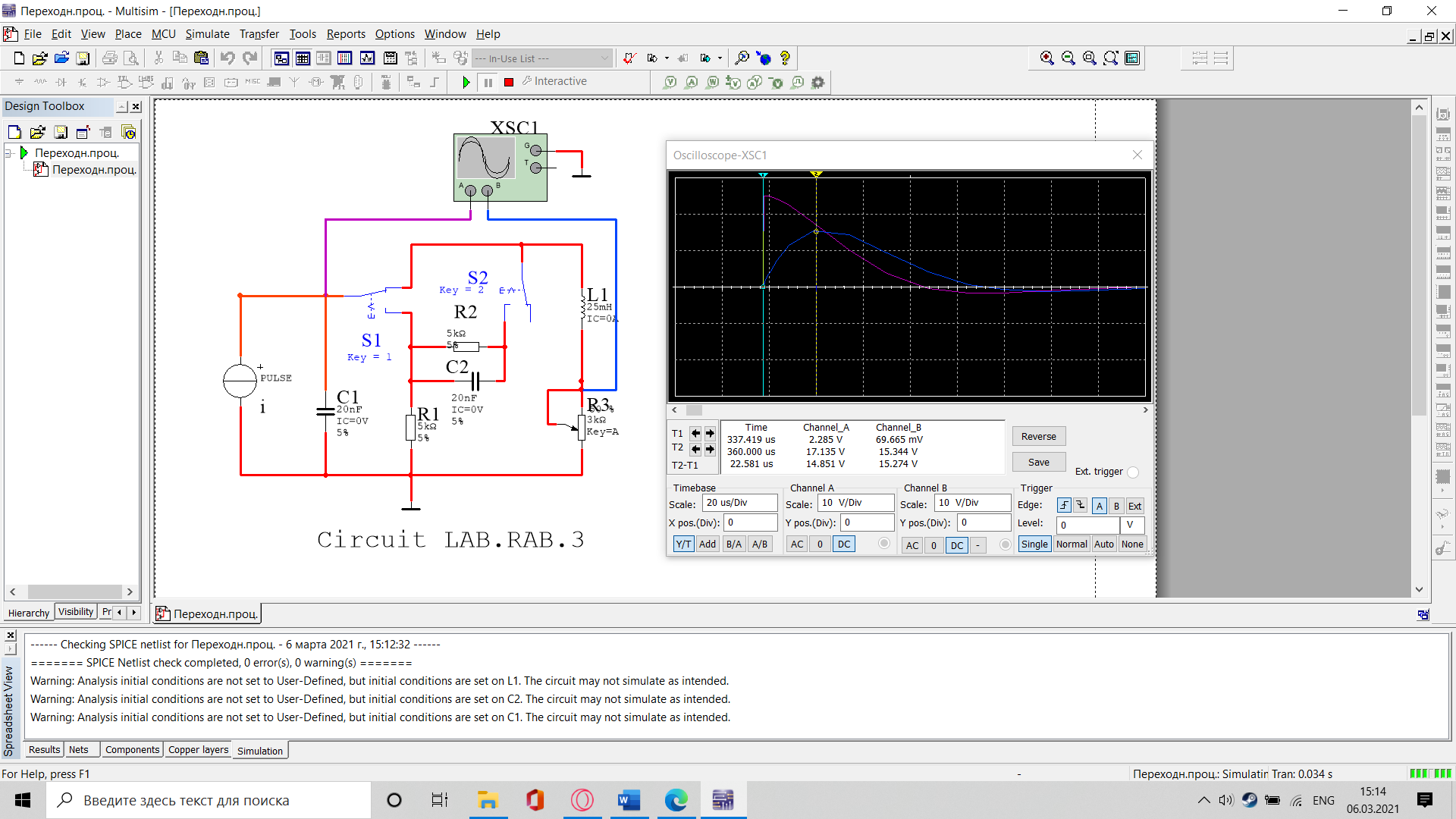 Колебательный(R17%) 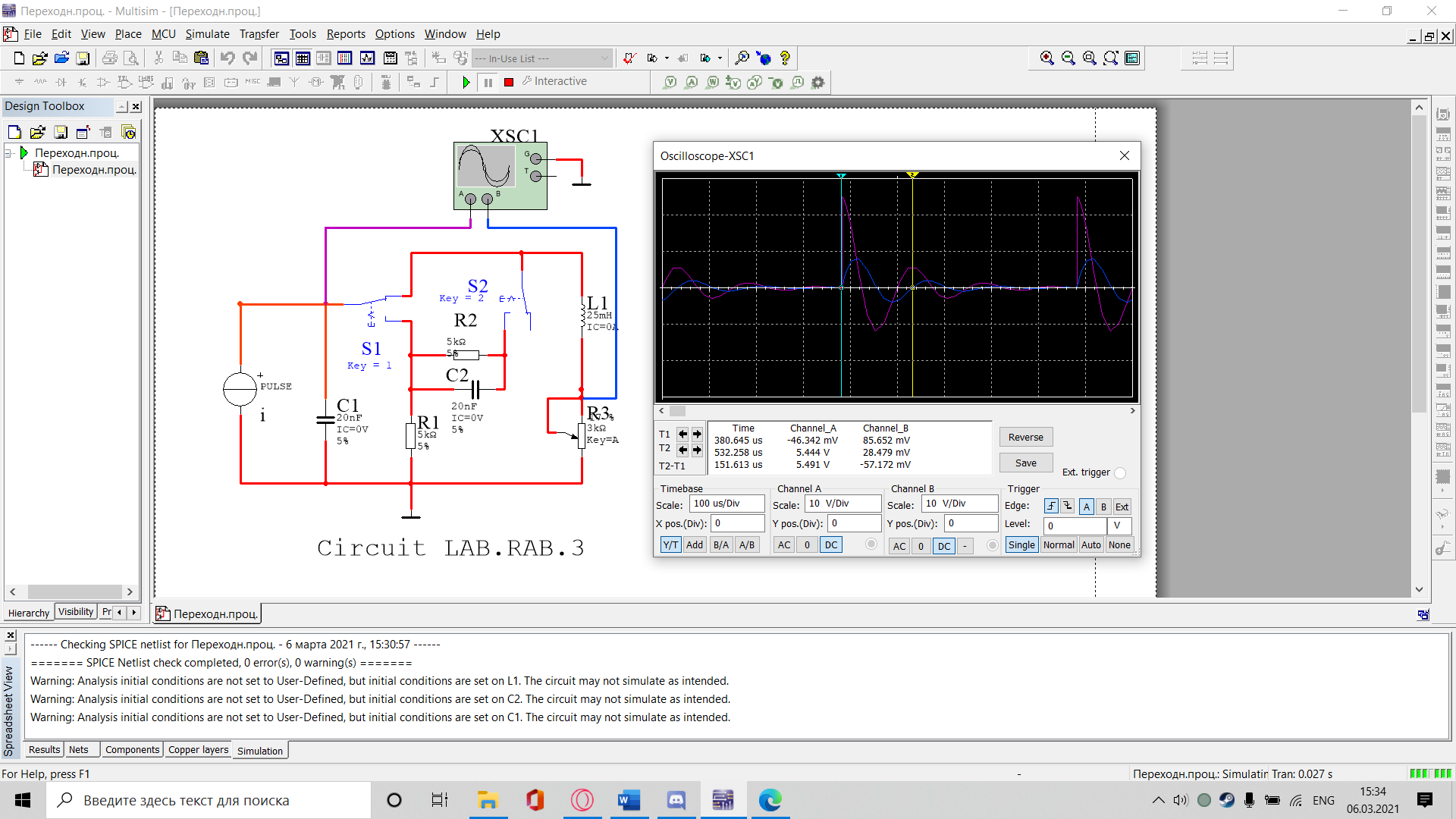 Критический(R60%) 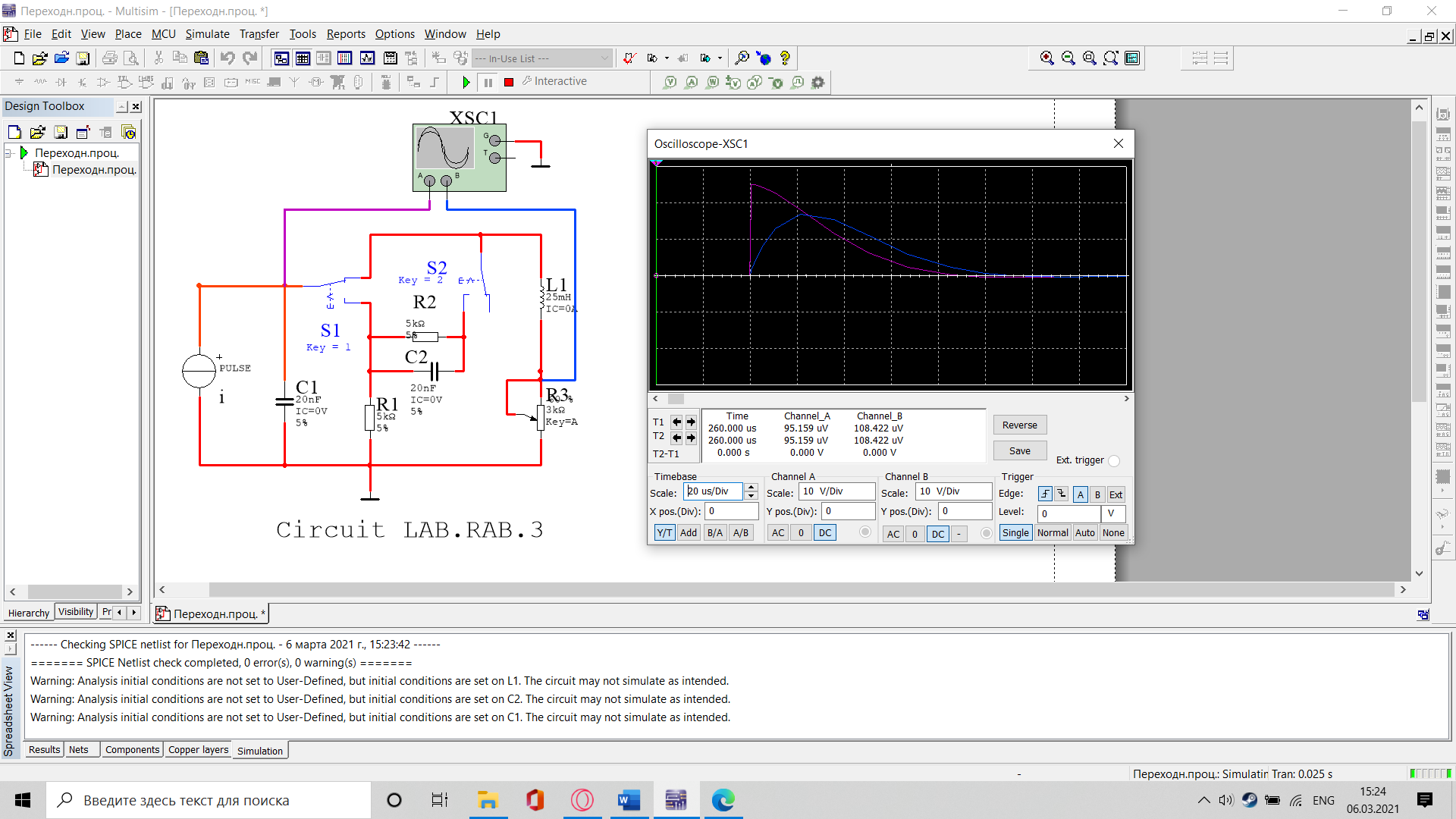 R=30Ом 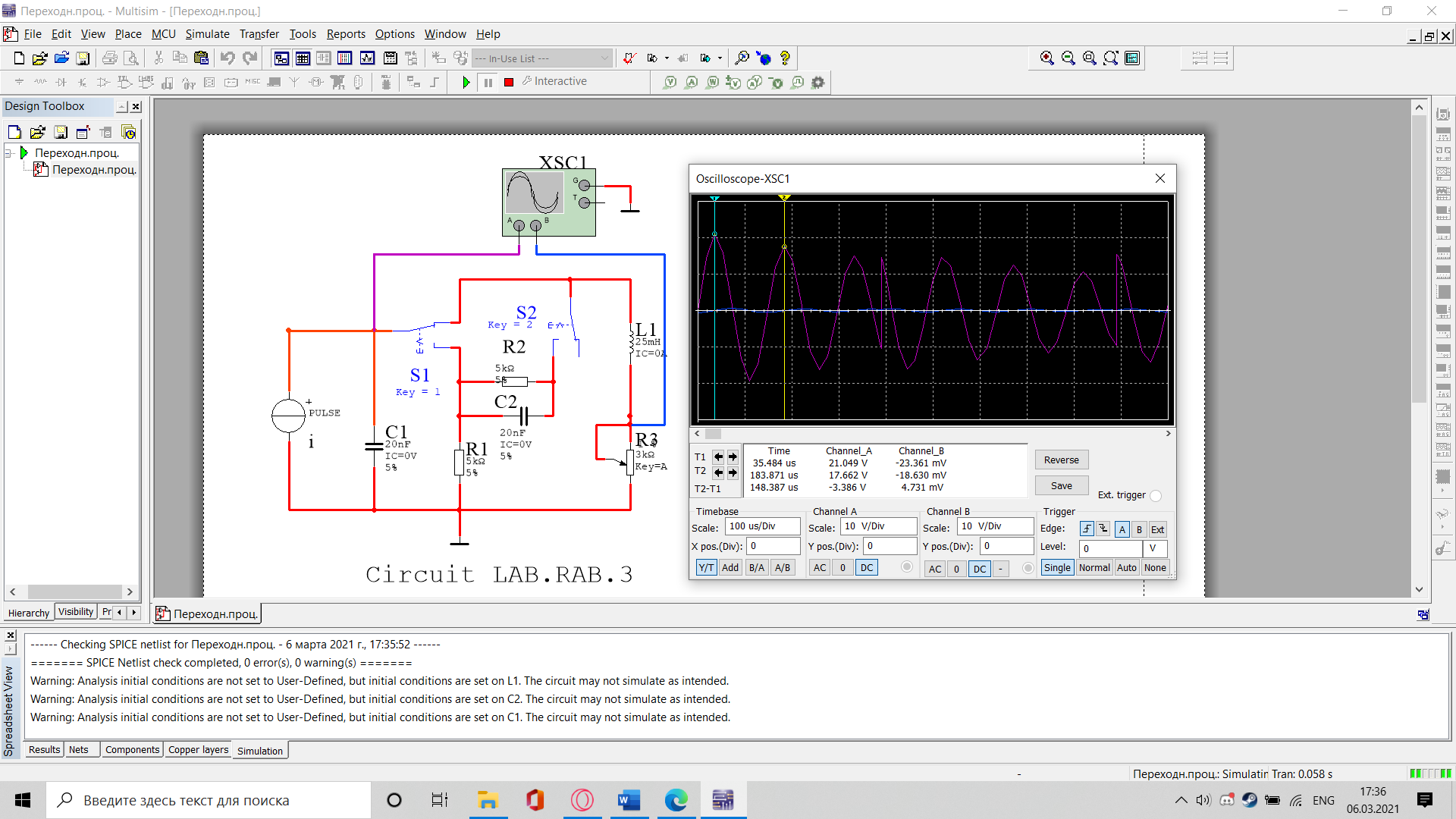 Рассчитаем 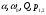 для всех режимов для всех режимов
3.2.3. Исследование свободных процессов в цепи третьего порядка 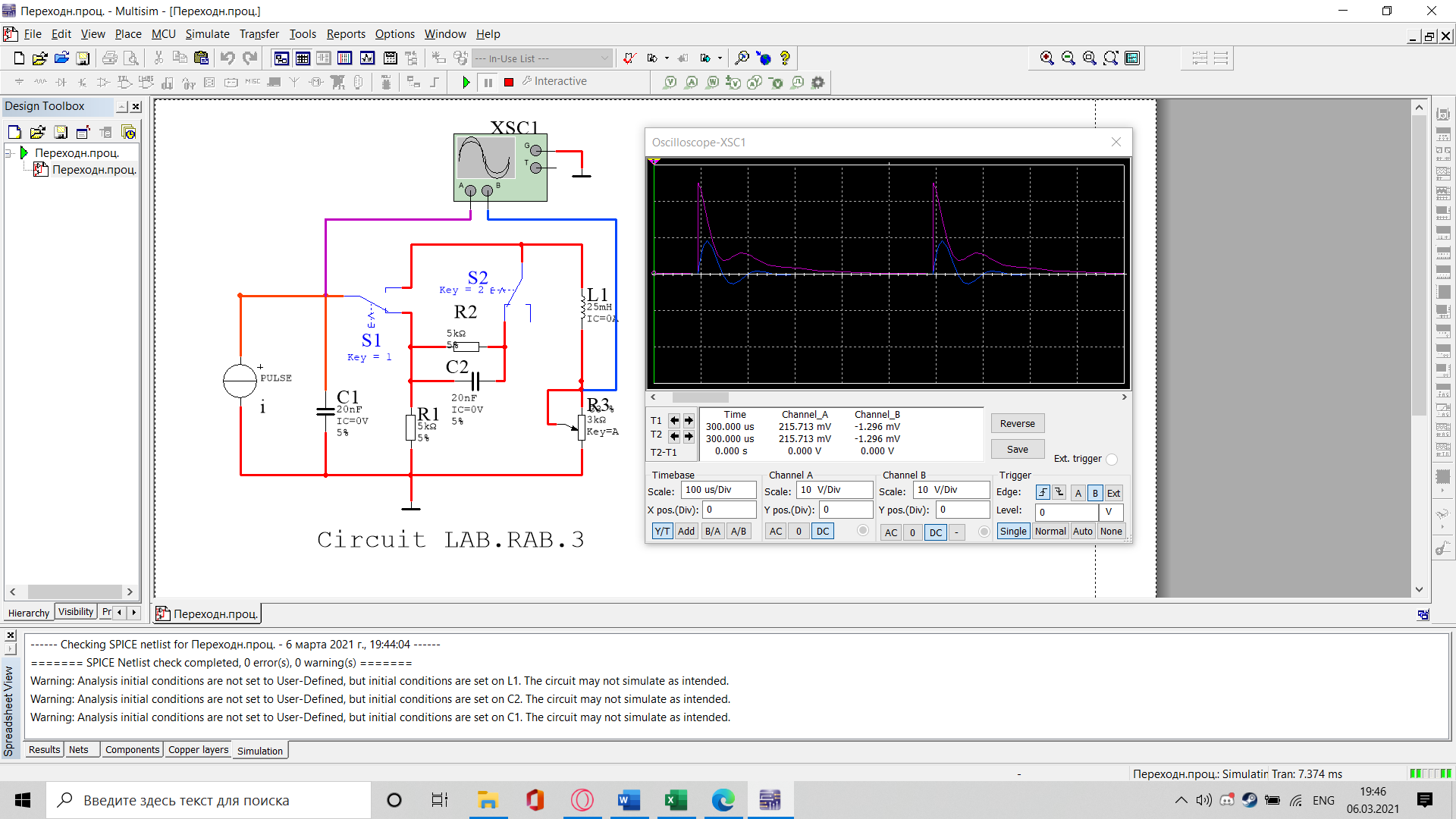 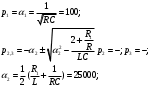 p2 = 4.3 * 106 p3 = -4.425 * 106 Вывод : Выполнил лабораторную работу на исследование свободных процессов в электрических цепях, изучил связи между видом свободного процесса в электрической цепи и расположением собственных частот (корней характеристического уравнения) на комплексной плоскости. Каким аналитическим выражением описывается осциллографируемый процесс в цепи первого порядка? U(t) = A1ep1t Как по осциллограмме определить собственную частоту цепи первого порядка? Соответствует ли она теоретическому расчету по (3.1)? 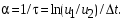 Величина собственной частоты практические совпадает с теоретическим расчетом. Какими аналитическими выражениями (в общем виде) описываются графики процессов в цепях второго порядка. U(t) = A1ep1t + A2ep2t апериодический 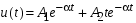 критический критический 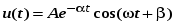 колебательный колебательныйКак определить по осциллограмме, снятой при 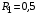 кОм, собственные частоты цепи второго порядка? Соответствуют ли они теоретическому расчету, выполненному по (3.2)? кОм, собственные частоты цепи второго порядка? Соответствуют ли они теоретическому расчету, выполненному по (3.2)?P12 = -α± 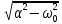 ; ; 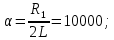 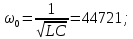 P12 = -10000 ± 43588 *j; Каковы теоретические значения собственных частот при R1 = 3кОм и 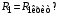 Соответствуют ли осциллограммы этим значениям и почему? Соответствуют ли осциллограммы этим значениям и почему?P12 = -α± 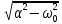 ; ; 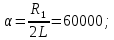 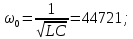 P12 = -60000 ± 43588 *j; Какова добротность контура при 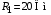 и и 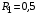 кОм? кОм?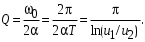 При R1 = 20 кОм 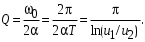 Q = 6.8; При R1 = 0.5 кОм 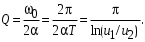 Q = 2.27 Каким аналитическим выражением описывается полученный график свободного процесса в цепи третьего порядка? U(t) = A1ep1t + A2ep2t + A3ep3t Дальнейшее увеличение порядка цепи после 2 порядка к качественно новым явлениям не приводит. Каково значение собственных частот цепи третьего порядка 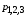 , вычисленных по (3.3)? Соответствует ли им осциллограмма и почему? , вычисленных по (3.3)? Соответствует ли им осциллограмма и почему?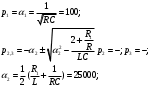 |