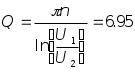Исследование свободных процессов в электрических цепях

• Название: Исследование свободных процессов в электрических цепях
• Дата: 18.10.2020
• Размер: 1.08 Mb.
• Имя файла: LAB3.doc
• Тип: Исследование; #143672

- -

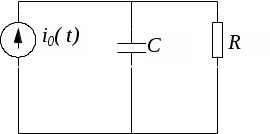
Исследование свободных процессов в электрических цепях.
Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением свободных частот (корней характеристического уравнения) на комплексной плоскости; приближенная оценка собственных частот и добротности контура по осциллограммам.
1. Исследование свободных процессов в цепи первого порядка.

В цепи (рис.1) мкФ; кОм.

Рис. 1.

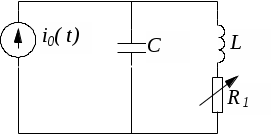
Расчет собственной частоты цепи.

с^-1

Из осцилограммы, рис. 1, собственная частота цепи равна

t=0.85*10^-3 с Þ p₁=-1/t=1.18*10³ c^-1

Свободный процесс имеет вид:



Диаграмма расположения собственной частоты на комплексной плоскости: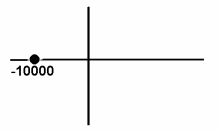



2. Исследование свободных процессов в цепи второго порядка.

В цепи (рис. 2) мкФ; мГн.

Рис. 2.

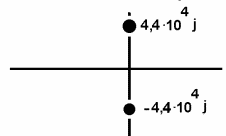
Колебательный режим R₁=0.5 кОм

Теоритический расчёт собственной частоты: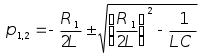







Из осцилограммы, Рис. 2, собственные частоты цепи равны: T=0.13 мс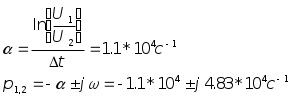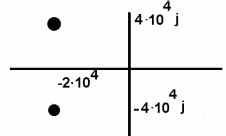




Рассчитаем добротность контура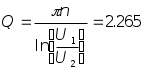



Апереодический режим кОм

Теоритический расчёт собственной частоты: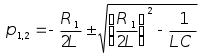



p₁=-2.3*10⁵ c^-1 p₂=-1*10⁴ c^-1

Диаграмма расположения собственных частот:

Осцилограмма представлена на Рис. 3.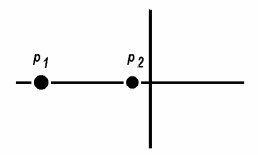

Критический апериодический режим R₁=1.5 кОм

p₁=p₂=-R₁/2L=-4.4*10⁴ c^-1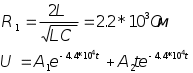


Осцилограмма представлена на Рис. 4.

Диаграмма расположения собственных частот: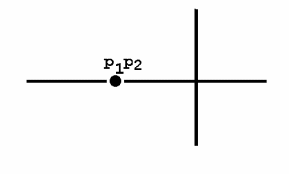


Незатухающий колебательный режим. R₁=0.

Теоритический расчёт собственной частоты: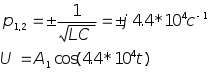



Из осцилограммы, Рис. 5, собственные частоты цепи равны.

Период судя по осцилограмме, равен: Т=0.12 мс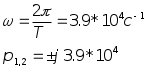



Диаграмма расположения собственных частот:

Добротность

3. Исследование свободных процессов в цепи второго порядка.

Дана цепь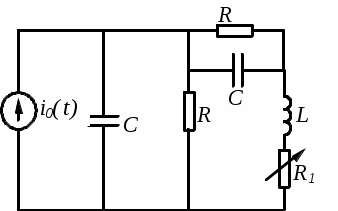



кОм, кОм, мкФ, мГн, кГц.

Теоритический расчёт собственных частот.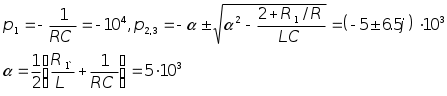




Из осциллограммы, Рис. 6, собственных частот цепи.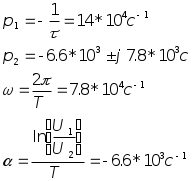



Диаграмма расположения собственной частоты.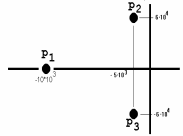



Вывод. Форма реакции цепи зависит от вида собственных частот: если собственные частоты вещественные — апериодический режим, комплекстно-сопряженные — периодический режим, кратные — критический апериодический режим.

Так как изучались не идеальные, а реальные цепи результаты аналитических расчетов не совпадают в данными осциллограмм. При аналитических расчетах не учитывались сопротивления проводов, паразитные емкости и индуктивности. Несовпадение теоретических и экспериментальных данных вызвано также неточностью измерений и неточностью номиналов элементов.