Исследование систему автоматического регулирования на устойчивость с помощью критерия Гурвица. Исследование устойчивости системы с использованием критерия Гурвица по дисциплине Основы теории управления
 Скачать 421.18 Kb. Скачать 421.18 Kb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ им. проф. М.А. БОНЧ-БРУЕВИЧА» (СПбГУТ) ОТЧЁТ по лабораторной работе № 1 на тему: «Исследование устойчивости системы с использованием критерия Гурвица» по дисциплине «Основы теории управления» Цель работы: исследовать систему автоматического регулирования на устойчивость с помощью критерия Гурвица. Ход работы: Дано: Схема системы регулирования скорости двигателя               X вых X вх УМ ЭУ ТГ Эдв   ЭУ – электронный усилитель Кэу(р) = К1; УМ – усилитель мощность Кум(р) =  ; ;Эдв – электродвигатель Кэдв(р) =  ; ;ТГ – тахогенератор; Т – коэффициент (инерционность); Ктг(р) = К4; T1 = 0.1, T2 = 0.2, T3 = 0.01 Найти: Ккр используя критерий Гурвица. Ко = 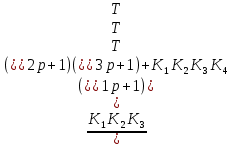 – общая передаточная функция – общая передаточная функцияЗнаменатель – характеристический полином. T1T2T3p3+( T1T3+T2T3+T1T2)p2 + (T1+T2+T3)p + 1+  ; ;Следовательно: а0 = T1T2T3 = 0.0002 а1= T1T3+T2T3+T1T2 = 0.023 а2= T1+T2+T3 = 0.31 а3= 1 +  ; ;Находим предпоследний диагональный минор и подставляем известные коэффициенты в формуле а1а2 – а0а3: 0.00693-0.0002К = 0; Кобщ=34.65 – критическое значение разомкнутой системы; Моделируем схему системы в программе CLASSIC-3.2(рис.1). Количество звеньев станет равно четырем, так как переходную функцию усилителя мощности разделим на две функции (  ). ). Рис.1 Анализируем изменение передаточных функций при установке К. Изначально установим значение меньше Кобщ. Корни характеристического уравнения находятся в левой полуплоскости, имеют отрицательные вещественные части, тогда система будет устойчива, переходный процесс монотонный (рис. 2)  Рис.2 Заметим, что при увеличении К разомкнутой системы процесс становится колебательным. При этом корни находятся ближе к минимой оси.(рис.3) 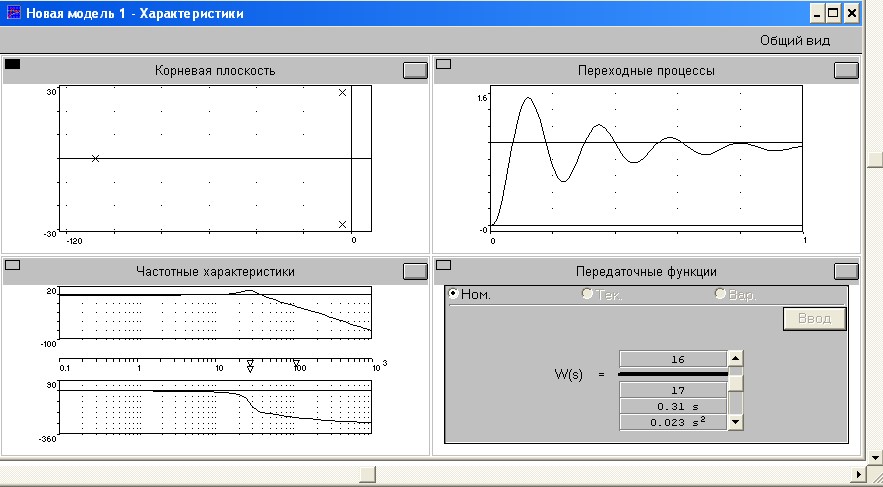 Рис.3 Установим критическое значение Кобщ = 34.65(рис. 4) разомкнутой системы. При критическом значении процесс становится незатухающим колебательным. При этом корни характеристического уравнения находятся на мнимой оси плоскости.  Рис.4 Установим значение больше критического (рис.5). Корни характеристического уравнения располагаются в правой полуплоскости, значит система становится неустойчивой, переходный процесс – расходящийся.  Рис.5 Вывод: в результате выполнения лабораторной работы была смоделирована система регулирования скорости двигателя, с помощью программы CLASSIC, которая помогает увидеть изменения системы и ее процессов. Санкт-Петербург 2021 |
