Критерий устойчивости. Критерий+устойчивости+Гурвица+25.02. Критерий устойчивости Гурвица

• Название: Критерий устойчивости Гурвица
• Анкор: Критерий устойчивости
• Дата: 26.02.2022
• Размер: 108.02 Kb.
• Имя файла: Критерий+устойчивости+Гурвица+25.02.docx
• Тип: Документы; #374188

1. 
   _{Критерий} устойчивости Гурвица
   

Для исследования устойчивости линейной системы достаточно найти корни его характеристического полинома. Если все корни имеют отрицательные вещественные части (находятся в левой полуплоскости, слева от оси) такой полином называется устойчивым, соответствующая линейная система устойчива. Полиномы, имеющие хотя бы один корень с положительной вещественной частью (в правой полуплоскости) называется неустойчивым.

На ранней стадии развития ТАУ актуальной была задача определения устойчивости полинома без вычисления его корней. Поэтому важное значение приобретают правила, которые позволяют определить устойчивость системы без вычисления корней. Эти правила называют критериями устойчивости. С помощью критериев устойчивости можно установить, устойчива система или

нет, выяснить как влияют на устойчивость те или иные параметры и структурные изменения в системе. Критерии устойчивости могут быть разделены на алгебраические и частотные.

Из алгебраических критериев устойчивости наиболее широкое распространение получили критерии устойчивости Рауса и Гурвица.

Алгебраические критерии устойчивости позволяют судить об устойчивости системы по коэффициентам характеристического уравнения:

1

0

2
a pⁿ ap^n1  a

p^n2   a

 0 .

0
Прежде всего для устойчивости все коэффициенты a_i

должны быть

положительными. Это необходимое условие устойчивости полинома:

a₀  0, a₁  0, ....a_n 0 .

Для систем первого и второго порядков необходимое условие устойчивости является и достаточным условием устойчивости, поскольку при положительных коэффициентах характеристического уравнения все его корни является левыми, т.е. они расположены в левой полуплоскости комплексной плоскости.

Однако при

n 2

это условие недостаточно, если полином имеет

комплексно-сопряженные корни. Для систем третьего и высших порядков положительность коэффициентов характеристического уравнения является необходимым условием устойчивости, но не достаточным. В это случае все вещественные корни характеристического уравнения левые, а комплексные же корни могут быть и правыми, т.е. расположенными в правой полуплоскости комплексной плоскости.

Критерий устойчивости Гурвица позволяет по коэффициентам характеристического уравнения без вычисления его корней сделать вывод об устойчивости системы.

Критерий устойчивости Гурвица использует матрицу размером составленную из коэффициентов полинома.

n n

Матрица Гурвица строится следующим образом: по главной диагонали определителя слева направо выписывают все коэффициенты

характеристического уравнения от

а₁ ^до а_n

в порядке возрастания индексов.

Столбцы вверх от главной диагонали дополняют коэффициентами характеристического уравнения с последовательно возрастающими индексами, а столбцы вниз – коэффициентами с последовательно убывающими индексами. На место коэффициентов с индексами больше n (n – степень характеристического уравнения) и меньше нуля проставляют нули.

 _n

a₃ a₂ a₁ a₀

a1

a0

0 0 ... 0

... 0

a₅ a₄ a₃ a₂

... 0

a₇ a₆ a₅ a₄

... 0

...

...

...

...

...

...

0

0

0 _.

0

...

a_n

(11.4)

Отчеркивая в главном определителе Гурвица, как показано пунктиром, диагональные миноры, получаем определители Гурвица низшего порядка:

  a

• 
  0;
  

  <sup>a1

a3</sup>  aa

• 
  aa
  

• 
  0;
  

^{1 1} 2
a₁ a₃ a₅

a₀ a₂

1 2 0 3

  a a a  a(aa

• 
  aa)  a²a
  

• 
  0 …;
  

  a

• 
  0.
  

3 0 2 4

0 a₁ a₃

3 1 2 0 3 1 4

n n n1

Номер определителя определяется номером коэффициента по диагонали матрицы Гурвица.

Критерий Гурвица позволяет получать условия устойчивости для систем любого порядка и формулируется следующим образом: для того чтобы корни характеристического уравнения линейной системы имели отрицательные вещественные части, а система была устойчивой, необходимо и достаточно при положительности всех коэффициентов характеристического уравнения, чтобы все диагональные миноры матрицы Гурвица были положительны.

Рассмотрим алгебраические критерии устойчивости. Критерий устойчивости Гурвица (1895 г.) позволяет судить об устойчивости линейной системы по коэффициентам характеристического уравнения.

Покажем, что необходимым и достаточным условием устойчивости систем I и II порядка является положительность всех коэффициентов характеристического уравнения.

Например. 1. Характеристическое уравнение первого порядка

а₀ p а₁  0 ^.

Условие устойчивости: оба коэффициента

a₀  0,

a₁  0,

единственный

корень pотрицательный

p   ^a1 , и система устойчива.

a₂

2. 
   Характеристическое уравнение второго порядка: a
   

p²  ap a

 0,

• 
  a
  

0 1 2

Корень уравнения:

^p1,2

_ 1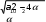

2a₀

   j .

Условие устойчивости

a₀  0,

a₁  0, a₂  0.

2. 
   Характеристическое уравнение третьего порядка
   

1

0
ap³  a

p²  a

p a₃

 0 .

2
Необходимые и достаточные условия устойчивости:

a₀  0,

a₁  0,

a₂  0, a₃  0.

a₁ a₃

Матрица Гурвица:

0


1

3
a a

a₀ a₂ 0

0 a a

• 
  0 ,
  

₁  a₁

• 
  0;
  

 ₂ 


a
0

 a₁a₂


a
2

• 
  a₀ a₃
  

• 
  0.
  

1 3

2. 
   Характеристическое уравнение четвертого порядка:
   

1

0

2
ap⁴  ap³  a

p²  a

p a₄

 0 .

3
Необходимые и достаточные условия устойчивости:

a₀  0,

a₁  0,

a₂  0,

a₃  0,

a₄  0.

2
Матрица Гурвица:

a₁ a₃ 0

a₀ a₂ a₄

0 a₁ a₃

0 a₀ a₂

0

⁰  0,

0

a₄
₁  a₁

• 
  0,
  

  ^a1 a₀
a₃


a
 a₁a₂

2

• 
  a₃ a₀
  

• 
  0;
  

a₁

  a₀

a₃ 0

a₂ a₄
 a₃
(a₁a₂

• 
  a₃ a₀
  

1

4
)  a²a

• 
  0.
  

0 a₁

При

a₃

a_n 0 ,
^n ^{ a}n^n1
, то для проверки устойчивости системы

достаточно найти только определители Гурвица ₁ до  _n1 .

При

n 5

процесс раскрытия определителей становиться довольно

трудоемким и громоздким. Поэтому критерий устойчивости Гурвица обычно

применяют при

n 4 ^{. При}

n 5

целесообразно применять формулируемый

ниже критерий устойчивости Льенара-Шипара, либо при использовании критерия устойчивости Гурвица переходить к численным методам с использованием ЭВМ. Критерий устойчивости Льенара-Шипара (1914г) является модификацией критерия Гурвица.

Доказано, что в том случае, когда все коэффициенты

характеристического уравнения положительны

a₀  0,

a₁  0,…

a_n  0 , из

того факта, что положительны все определители

₁, ₃ , ₅...

с нечетными

индексами, следует и положительность определителей индексами, и наоборот.

₂ , ₄ , ₆ ...

с четными

Таким образом, для того чтобы линейная система была устойчива,

необходимо и достаточно, чтобы выполнялись следующие неравенства:

a₀  0, a₁  0,...,a_n  0 _

или

a₀  0, a₁  0,...,a_n 0 _

. (11.5)




₁  0, ₃  0, ₅  0,..





₂  0, ₄  0, ₆  0,..

Последняя формулировка называется критерием устойчивости Льенара- Шипара, который требует раскрытия меньшего числа определителей, чем обычный критерий Гурвица.