Практика збір та обробка. Исследование вариационного ряда по результатам анализа 100 проб гранитов на один из элементов (табл. 3)

• Название: Исследование вариационного ряда по результатам анализа 100 проб гранитов на один из элементов (табл. 3)
• Дата: 10.10.2018
• Размер: 150.03 Kb.
• Имя файла: Практика збір та обробка.docx
• Тип: Исследование; #53044
• страница: 3 из 3

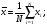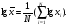Выборочные оценки дисперсии содержания и их логарифмов вычисляют следующим образом: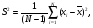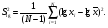



Показатели асимметрии: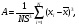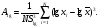



Показатели эксцесса: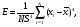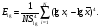



Для проверки согласованности эмпирического распределения данных выборки с теоретическим нормальным вычисляется критерий: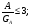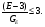



для логнормального: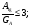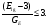



где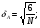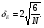



N - объем выборки.

3. Необходимое число проб для оценки средних содержаний по выборке с заданной точностью определяют по формуле: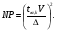



где NP - число проб для оценки средних содержаний;

∆ - заданная точность оценки среднего;

t_α,k - значение критерия Стьюдента для заданного уровня значимости α и данного числа степеней свободы f (см. приложение 2). Уровень значимости и доверительная вероятность (Р) соотносятся как:

Р = (1 - α) 100%, V - коэффициент вариации для нормально распределенных данных вычисляется по формуле: 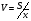100%, а для логнормальных:



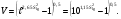Точное значение NP определяется последовательным приближением (итерациями), так как число степеней свободы f в свою очередь зависит от NP (f = NP - 1). Сначала вычисляют приближенное значение NP при t _{α, k} бесконечным числом степеней свободы f=∞. Затем значение t _{α, k} уточняют в соответствии с приближенным значением NР. Уточнение значения NР проводят до тех пор, пока округленное до целых число проб перестанет изменяться.
Приложение 2
Допустимые значения критерия Стьюдента t _{α, k} при данном числе степеней свободы и уровне значимости α.
Таблица

f	α = 0,05	α = 0,01	f	α = 0,05	α = 0,01	f	α = 0,05	α = 0,01
1	12,71	63,66	12	2,18	3,05	23	2,07	2,81
2	4,30	9,93	13	2,16	3,01	24	2,06	2,80
3	3,18	5,84	14	2,15	2,98	25	2,06	2,79
4	2,78	4,60	15	2,13	2,95	26	2,06	2,78
5	2,57	4,03	16	2,12	2,92	27	2,05	2,77
6	2,45	3,71	17	2,11	2,90	28	2,05	2,76
7	2,37	3,50	18	2,10	2,88	29	2,05	2,76
8	2,31	3,36	19	2,09	2,86	30	2,04	2,75
9	2,26	3,25	20	2,09	2,85	40	2,02	2,70
10	2,23	3,17	21	2,08	2,83	60	2,00	2,66
11	2,20	3,11	22	2,07	2,82	120	1,98	2,62
							1,96	2,58

Таблица

Значения критерия Пирсона (х²)

f	α = 0,05	α = 0,01	f	α = 0,05	α = 0,01
1	3,841	6,635	11	19,675	24,725
2	5,991	9,210	12	21,026	26,217
3	7,815	11,341	13	22,362	27,688
4	9,488	13,277	14	23,685	29,141
5	11,070	15,086	15	24,996	30,578
6	12,592	16,812	16	26,296	32,000
7	14,067	18,475	17	27,587	33,409
8	15,507	20,090	18	28,869	34,805
9	16,919	21,666	19	30,144	36,191
10	18,307	23,209	20	31,410	37,566