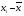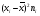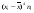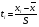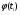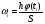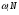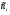Практика збір та обробка. Исследование вариационного ряда по результатам анализа 100 проб гранитов на один из элементов (табл. 3)
 Скачать 150.03 Kb.
|
|
Практическая работа №1 Рассмотрим последовательность составления и исследование вариационного ряда по результатам анализа 100 проб гранитов на один из элементов (табл.3): Таблица 3
Минимальное содержание изучаемого элемента равно 0,60; максимальное - 8,40%. Определим по формуле / 1 / длину интервала группировки 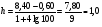 Число этих интервалов определяется знаменателем формулы / 1 / и в дан ном случае равно 9. Границы частичных интервалов можно выбрать такими: 0,0-1,0; 1,0-2,0; 2,0-3,0; 3,0-4,0; 4,0-5,0; 5,0-6,0; 6,0-7,0; 7,0-8,0; 8,0-9,0. Условимся, что значения показателя в выборке, совпадающие с грани частичных интервалов, будем относить в интервал меньших значении. Теперь приступаем к разнесению данных по классам (интервалам). В результате получим следующий вариационный ряд: Таблица 4
После разнесения данных по классам необходимо выполнить проверку со ответствия суммы частот с объемом выборки: 1+3+11+21+31+23+7+2+1=100 N = 100 Ряд накопленных частот для нашего примера имеет вид: Таблица 5
Перейдем к графическому изображению ряда. На рис. 3 показан полигон распределения вариационного ряда, построенный согласно данным табл. 4. По оси абсцисс отложены середины частичных интервалов, а по оси ординат - частоты. На рис. 4 показана гистограмма распределения того же вариационного ряда. По оси абсцисс отложены границы частичных интервалов, на ко торых затем построены прямоугольники, высотой, соответствующей часто те частичного интервала. На рис. 5 показана кривая накопленных частот нашего вариационного ряда, построенная в соответствии с данными табл. 5. Теперь выполним аналитическое исследование вариационного ряда. Ис числение статистик удобно производить после заполнения таблицы такого вида: Таблица 6
По результатам суммирования Σ колонок таблицы 6 получим следующие статистики: 1) среднее: 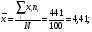 2) дисперсия: 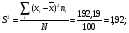 3) среднеквадратичное отклонение: 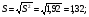 4) коэффициент вариации: 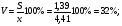 5) показатель асимметрии: 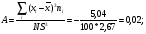 6) показатель эксцесса:  7) медиана: 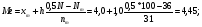 8) мода: 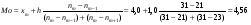 Практическая работа №2 Сравнение выборочного распределения с теоретическим Многие задачи, решаемые статистическими методами, требуют выполнения условия распределения изучаемого показателя по какому-то чаще всего нормальному теоретическому закону. Так, например, широко рас пространенные в геологии задачи определения необходимого числа раз ведочных скважин, расчет погрешностей подсчета запасов, установление зависимостей между показателями, требует подчинения выборочных дан ных нормальному закону распределения. Проверка гипотезы о нормальном законе распределения выборочных данных может быть проведена по пока зателям асимметрии и эксцесса. Схема проверки такова; - выдвигается нулевая гипотеза HO: распределение выборочных данных соответствует нормальному закону; - критерием для проверки выдвинутой гипотезы служит выполнение следующих неравенств:  ;  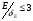; / 25 /- если полученные значения  и 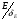 не больше 3, то нулевую гипотезу принимаем, т.е. в этом случае выборочные данные подчинены нормальному закону распределения. Если же или 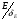больше 3, то для выборочных данных следует подбирать другой закон распределения Пример. Проверим данные по гранитам, приведенные в предыдущем примере, на подчинение нормальному закону распределения. Выдвигаем нулевую гипотезу HO: содержание элемента в гранитах подчинено нормальному закону рас пределения. По вычисленным данным A = -0,02; E = 0,35. Для показателя асимметрии: 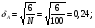 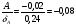 <3Для показателя эксцесса: 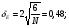 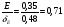 <3Таким образом, принимается гипотеза о нормальности распределения содер жания элемент в гранитах, Более общим критерием для проверки согласованности эмпирического и теоретического законов распределения являются критерии, основанные на сравнении выборочных и теоретических частот различных распределе нии. Наиболее широко применяемыми из них являются λ - критерий Колмо горова-Смирнова и χ2 - критерий Пирсона. Прежде всего для применения этих' критериев необходимо рассчитать частоты теоретического закона распределения, который более всего подходит к гистограмме (полигону) вариационного ряда и выдвинут в качестве нулевой гипотезы. Рассмотри расчет частот нормального распределения. Он осуществляется по формуле: 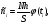 / 26 /где 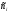 - теоретические частоты нормального закона распределения; N - объем выборки; h - ширина интервала группировки данных; S - среднеквадратичное отклонение; 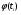 - табличное значение функции нормального распределения. 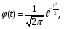 / 27 /где  .Рассчитали теоретические частоты для данных табл. 3. По ранее произведенным вычислениям примера 1 имеем следующие данные  S = 1,39; h = 1,0; N = 100. Результаты вычислений в табл. 7.Последняя колонка таблицы 7, содержащая теоретические частоты, получена округлением до целых единиц предыдущего расчетного столбца. Сумма полученных теоретических частот обязательно должна совпадать с суммой выборочных частот, т.е. с объемом выборки. Таблица 7
После вычисления частот выбранного теоретического распределения необходимо оценить степень согласия между эмпирическими и теоретически ми частотами. Критерий χ2, предложенный Пирсоном, определяют, по формуле: |
