oop курсовая. Исследование вычислительной эффективности объектноориентированных приложений

• Название: Исследование вычислительной эффективности объектноориентированных приложений
• Дата: 12.01.2023
• Размер: 0.82 Mb.
• Имя файла: oop курсовая.docx
• Тип: Исследование; #883628
• страница: 2 из 9

ПОСТАНОВКА ЗАДАЧИ

Основная задача курсовой работы – разработать процедурное и объектно-ориентированное приложения, решающие задачу приближенного вычисления площади фигуры методом Монте-Карло, а также выполнить исследование вычислительной эффективности созданных приложений и представить результаты в виде таблиц, провести анализ и улучшить заданные характеристики качества приложений.

Вариант задания №12:

• 
  геометрическая фигура: anbkoe;
  
• 
  приложение 1: процедурное приложение на базе WPF/C#;
  
• 
  приложение 2: объектно-ориентированное приложение на базе WPF/C#.
  

Геометрическая фигура представляет собой прямоугольник, из которого вырезаны треугольник anb, треугольник kco и треугольник ode.(рис. 1).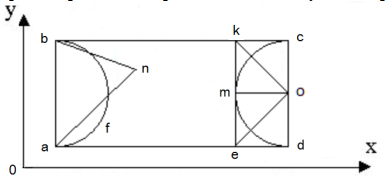



Рис. 1. Фигура anbkoeвнутри прямоугольника abcd

Исходными данными для каждого приложения являются координаты угловых точек фигуры. Для однозначного определения расположения фигуры сначала необходимо задать 3 точки: a, c, n. После чего вычисляются координаты точек o, k,e, dи b.

Для вычисления площади фигуры необходимо вначале вычислить площадь прямоугольника, описывающего заданную фигуру, после чего N раз сгенерировать два случайных числа для координат x и y, определяющие точку внутри заданной фигуры. Генерируемые случайным образом точки должны равномерно заполнять площадь прямоугольника. Для этого случайные числа должны иметь равномерное распределение.

Для каждой точки выполняется проверка, попала ли точка внутрь заданной фигуры. Если из N точек M точек оказалось внутри фигуры, а площадь прямоугольника равна S, то площадь фигуры будет приближенно равна .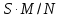

Так как площадь фигуры достаточно несложно определить по правилам геометрии, можно найти относительную погрешность приближенного вычисления площади заданной фигуры методом Монте-Карло.

Каждое приложение пять раз повторяет эксперимент и вычисляет площадь фигуры методом Монте-Карло для N= 10³, 10⁴, 10⁵, 10⁶, 10⁷ соответственно. В каждом из экспериментов определяется относительная погрешность вычисления площади (в процентах) и длительность вычисления (в миллисекундах).

После нахождения результатов экспериментов каждое приложение выдает на экран таблицу, содержащую значения относительной погрешности и длительности эксперимента, зависящих от величины N.

Задачами курсовой работы являются:

• 
  приобретение навыков решения вычислительных задач;
  
• 
  практическое освоение современных инструментальных систем разработки ПО;
  
• 
  сравнительный анализ вычислительной эффективности процедурных и объектно-ориентированных программ;
  
• 
  получение навыков создания программ на языке C# платформы Microsoft .NET Framework;
  
• 
  приобретение практических навыков оформления и выпуска документации в соответствии с требованиями стандартов (ЕСПД, UML).
  

2. РАЗРАБОТКА ТЕХНИЧЕСКОГО ЗАДАНИЯ

2.1. Анализ вариантов использования программы

Разрабатываемая программа по вычислению площади фигуры методом Монте-Карло должна предоставлять пользователю следующие возможности:

• 
  ввод координат (вручную или из контрольного примера);
  
• 
  нахождение площади фигуры методом Монте-Карло;
  
• 
  вывод на экран;
  
• 
  очистка полей ввода и таблицы результатов;
  
• 
  повторный расчёт;
  
• 
  выход.
  

Для наглядности и удобства восприятия строится так называемая «use case» диаграмма, на которой отображаются пользователи, а также варианты их действий. На диаграмме использованы виды отношений: включение, расширение и наследование (рисунок 2).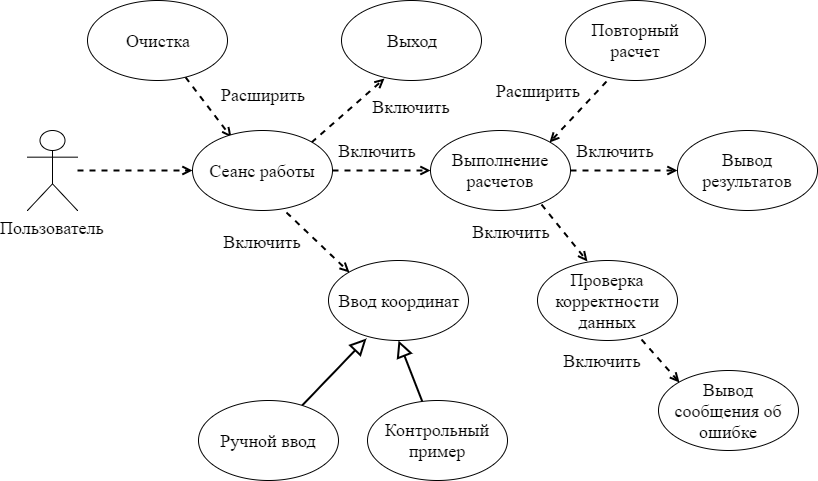



Рис. 2. Диаграмма вариантов использования приложений

Отношение расширения между вариантами использования обозначается пунктирной линией со стрелкой (вариант отношения зависимости), направленной от того варианта использования, который является расширением для исходного варианта использования. Данная линия со стрелкой помечается ключевым словом “extend” (“расширение”).

Отношение включения между вариантами использования обозначается пунктирной линией со стрелкой (стрелки идут от базового варианта) и иллюстрирует, что именно использует базовый вариант для выполнения операции, то есть, другими словами, включение используется тогда, когда базовый вариант не может быть выполнен без дополнительных условий и действий.