oop курсовая. Исследование вычислительной эффективности объектноориентированных приложений
 Скачать 0.82 Mb. Скачать 0.82 Mb.
|
2.2. Требования к приложениямУчитывая все вышеперечисленные задачи, можно составить перечень требований к приложениям, которому должны соответствовать программы: интерфейс программ должен быть интуитивно понятным пользователю; пользователь должен иметь возможность вводить данные как вручную, так и используя тестовый пример; программы должны выдавать ошибку пользователю, если тот ввёл некорректные значения; программы должны обладать высокой производительностью и эффективностью вычислений; пользователь должен иметь возможность выполнять расчёт несколько раз, другими словами, в программах необходимо возможность изменять входные данные и повторно выполнять расчёт площади фигуры. В зависимости от номера варианта, каждое приложение должно быть выполнено с использованием требуемых технологий. Для каждого приложения характерны следующие особенности, описанные ниже. Процедурное приложение на базе WPF/C#: тип: настольное приложение; графический интерфейс: Windows Presentation Foundation (WPF); язык программирования: C#; парадигма программирования: процедурная; параметр оптимизации: время выполнения. Объектно-ориентированное приложение на базе WPF/C#: тип: настольное приложение; графический интерфейс: WPF; язык программирования: C#; парадигма программирования: объектно-ориентированная; параметр оптимизации: время выполнения. 3.АНАЛИЗ АЛГОРИТМА РЕШЕНИЯ3.1. Метод Монте-КарлоМетод Монте-Карло – общее название группы численных методов, которые используются в решении огромного количества как математических, так и физических, химических, экономических задач. Метод заключается в многократном моделировании описанного математически процесса с использованием генератора случайных величин. На основе полученного набора случайных величин рассчитываются вероятностные характеристики процесса. Введем обозначения для координат точек (см. рис 1): 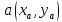 , , 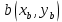 , , 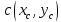 , , 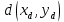 , , 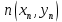 , , 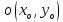 , , 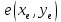 , , 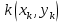 . .Для нахождения площади фигуры методом Монте-Карло необходимо следующее: 1) определить радиус окружности с центром 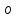 : :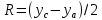 ; ;2) определить координаты точек: точки 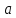 , , 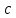 , , 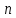 задаются, а координаты остальных вычисляются следующим образом: задаются, а координаты остальных вычисляются следующим образом: 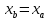 ; ; 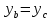 ; ; 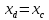 ; ; 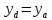 ; ; 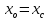 ; ; 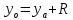 ; ; 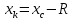 ; ; 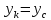 ; ; 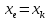 ; ; 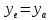 . .3) провести опыт, суть которого заключается в заполнении прямоугольника 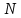 точками, с координатами точками, с координатами 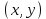 , где , где 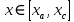 , , 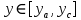 ; ;4) определить число точек M, попавших внутрь фигуры; 5) определить приближенную площадь фигуры методом Монте-Карло: 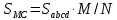 , ,где 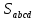 – площадь прямоугольника – площадь прямоугольника 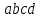 : :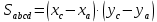 ; ;6) определить точную площадь фигуры: 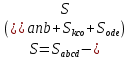 , ,где 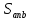 , , 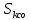 , , 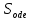 – площади треугольников – площади треугольников Площадь треугольника 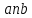 определяется по формуле половина произведения высоты на основание: определяется по формуле половина произведения высоты на основание: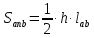 , ,где 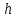 – высота треугольника – высота треугольника 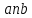 , , 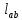 – длина стороны – длина стороны 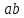 соответственно; соответственно;площадь треугольника 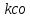 : :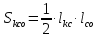 ; ;площадь треугольника ode: 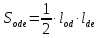 ; ;7) определить относительную погрешность по формуле: 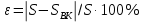 . . |
