oop курсовая. Исследование вычислительной эффективности объектноориентированных приложений

• Название: Исследование вычислительной эффективности объектноориентированных приложений
• Дата: 12.01.2023
• Размер: 0.82 Mb.
• Имя файла: oop курсовая.docx
• Тип: Исследование; #883628
• страница: 5 из 9

4.3. Системные требования

Для корректной работы приложения требуется:

• 
  операционная система Windows 10 и выше;
  
• 
  платформа .NET Framework 4.8 и выше;
  
• 
  архитектура 32-разрядная (х86)/64-разрядная (х64);
  
• 
  оперативная память 512 МБ и более;
  
• 
  устройства ввода: клавиатура, мышь.
  

4.4. Структура приложения

Структура программы представлена на рис. 6.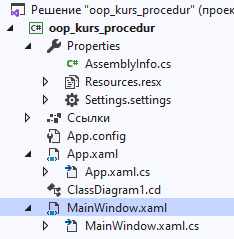



Рис. 6. Проект процедурного приложения

Настольное процедурное приложение на базе WPF/C# включает следующие файлы:

MainWindow.xaml – разметка формы;

MainWindow.xaml.cs – описания методов и события формы;

ClassDiagram1.cd – диаграмма класса MainWindow;

App.config – конфигурация программы;

App.xaml – объявление ресурсов, используемых по всему приложению.

4.5. Результаты работы

На рис. 7 представлены результаты работы настольного процедурного приложения на базе WPF/C#.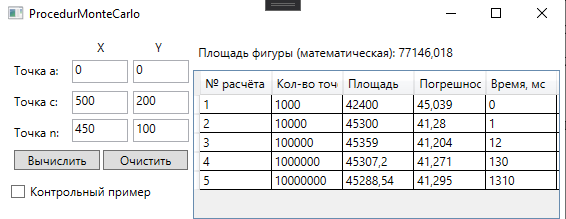



Рис. 7. Результаты работы настольного процедурного приложения на базе WPF/C#

5. ОБЪЕКТНО-ОРИЕНТИРОВАННОЕ ПРИЛОЖЕНИЕ НА БАЗЕ WPF/C#

5.1. Программные средства разработки

При создании процедурного приложения была использована среда разработки MS Visual Studio 2019. Данная среда разработки имеет удобный интерфейс и поддерживает все элементы, используемые в программе.

Для полноценной работы приложения потребовалось подключить несколько пространств имён, а также разработать собственные классы.

5.2. Логическое проектирование

Предметная область задания содержит следующие сущности:

Для эффективного проектирования для начала выделяются сущности предметной области. В данной задаче сущности:

• 
  точка;
  

• 
  треугольник;
  
• 
  прямоугольник;
  

Эти сущности можно реализовать посредством создания классов, а также при помощи использования уже встроенных в язык пространств имён. Так, для реализации точки можно использовать структуру пространства имён System.Windows, а именно Point.

Для треугольника и прямоугольника будут созданы классы MyTriangle и MyRectale.

Диаграмма классов настольного приложения WPF/С# представлена на рис.8.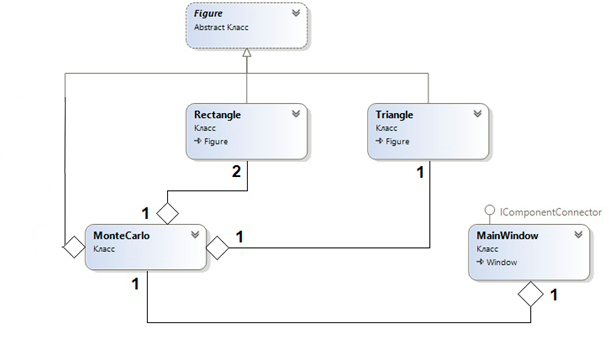



Рис. 8. Диаграмма классов объектно-ориентированного приложения

Диаграмма структуры Point, описывающей точку, представлена на рис. 9.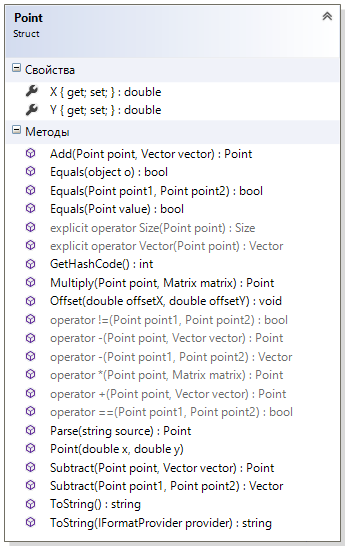



Рис. 9. Диаграмма структуры Point

Структура Point содержит следующие свойства:

public double X { get; set; } – координата x точки;

public double Y { get; set; } – координата y точки.

Структура Point содержит следующий конструктор:

public Point (double x, double y) – конструктор инициализации.

Абстрактный класс Figure, который используется для того, чтобы выделить общие свойства для производных классов Triangle и Rectangle содержит следующие методы:

abstract public bool IsInFigure(Point point) – проверка принадлежности точки данной фигуре;

abstract public double Square() – вычисление площади данной фигуры.

Диаграмма абстрактного класса показана на рис. 10.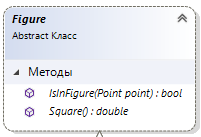



Рис. 10. Диаграмма абстрактного класса Figure

Класс Triangle, как и все создаваемые вручную классы, содержит три базовых конструктора:

public Triangle() – конструктор по умолчанию;

public Triangle (Point с, Point k, Point d) – конструктор инициализации;

public Triangle (Triangle triangle) – конструктор копии.

Так же у класса есть скрытые поля:

private Point a, n, b – точки a, n и b.

От абстрактного класса Figure тут присутствует реализация методов абстрактного класса:

override public bool IsInFigure(Point point) – проверка принадлежности точки данному треугольнику;

override public double Square() – вычисление площади данного треугольника.

На рис. 11 представлена диаграмма класса Triangle.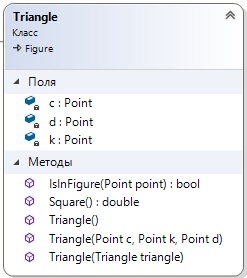



Рис. 11. Диаграмма класса Triangle

На рис. 12 представлена диаграмма класса Rectangle, описывающего прямоугольник и являющегося производным от Figure.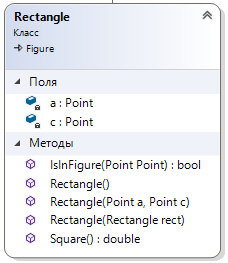



Рис. 12. Диаграмма класса Rectangle

Класс Rectangle содержит следующие поля:

private Point a, c – диагональные точки, определяющие прямоугольник.

Класс Rectangle содержит следующие конструкторы:

public Rectangle () – конструктор по умолчанию;

public Rectangle (Point a, Point c) – конструктор инициализации;

public Rectangle (Rectangle rect) – конструктор копии.

Класс Rectangle содержит следующие методы:

override public bool IsInFigure(Point point) – проверка принадлежности точки данному прямоугольнику;

override public double Square() – вычисление площади данного прямоугольника.

На рис. 14 представлена диаграмма класса MonteCarlo, описывающего реализацию метода Монте-Карло.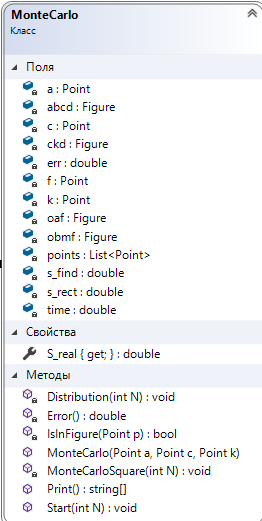



Рис. 14. Диаграмма класса MonteCarlo

Класс MonteCarlo содержит следующие поля:

private Point d, a, n, e – точки d, a, n и e соответственно;

private Figure ode – треугольник ode;

private Figure abcd – прямоугольник abcd;

private Figure kco – треугольник kco;

private Figure anb – треугольник anb;

private double s_find – площадь, вычисляемая методом Монте-Карло;

private double s_rect – площадь прямоугольника abcd;

private List points – множество генерируемых точек;

private double time – время, затрачиваемое на вычисление площади по N точкам;

private double err – погрешность вычисления площади.

Класс MonteCarlo содержит следующее свойство:

public double S_real {get; } – точная площадь искомой фигуры.

Класс MonteCarlo содержит следующий конструктор:

public MonteCarlo (Point A, Point C, Point n) – конструктор инициализации.

Класс MonteCarlo содержит следующие методы:

public void Start(int N) – выполнение основного алгоритма Монте-Карло;

private void Distribution(int N) – генерация точек;

private void MonteCarloSquare(int N) – вычисление площади фигуры по методу Монте-Карло;

private double Error() – вычисление относительной погрешности площади, определенной методом Монте-Карло;

private bool IsInFigure(Point p) – проверка точки на принадлежность искомой фигуре anbkoe;­

public string[] Print() – возврат результаты вычислений.

Для компонентов интерфейса заданы следующие обработчики событий:

private void Start_Btn_Click(object sender, RoutedEventArgs e) –нажатие кнопки «Вычислить»: начало выполнения программы;

private void WindowLoaded(object sender, RoutedEventArgs e) – загрузка окна Window;

private void Clear_Btn_Click(object sender, RoutedEventArgs e) –нажатие кнопки «Очистить»: очистка полей ввода и таблицы результатов;

private void Example_click(object sender, RoutedEventArgs e) – выбор варианта ввода данных «Контрольный пример»: автоматическое заполнение полей ввода данных значениями из примера;

На рис. 15 представлены схемы методов Start_Btn_Click (а) класса MainWindow, Start (б) и MonteCarloSquare (в) класса MonteCarlo.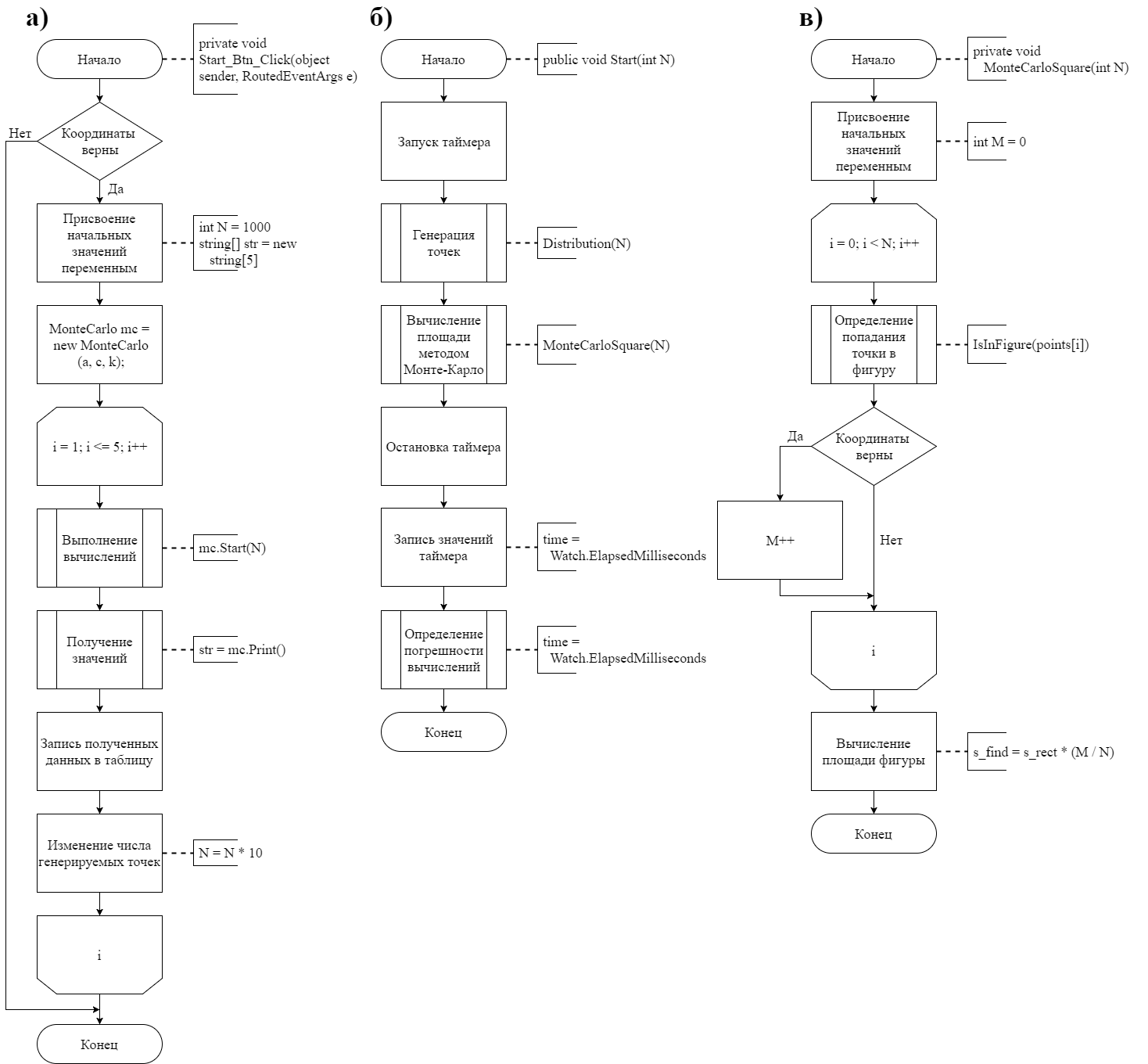



Рис. 15. Схемы методов Start_Btn_Click (а), Start (б) и MonteCarloSquare (в)

5.3. Описание программы

5.3.1. Общие сведения о приложении

Приложение, разработанное на языке программирования C# с использованием интерфейса Windows Presentation Foundation, создано для решения задачи по нахождению площади фигуры с заданными координатами методом Монте-Карло.

Приложение предоставляет пользователю возможность ввод координат трёх базовых точек вручную, а также предлагает выбрать тестовый пример задачи.

В приложении предусмотрены проверки на некорректный ввод данных, а также отсутствие ввода значений координат.

Приложение вычисляет площадь фигуры математически, а также методом Монте-Карло несколько раз для разного количества точек, заполняющих фигуру. Затем результаты выводятся в таблицу.

Пользователь имеет возможность изменения входных данных и повторного запуска расчётов

5.3.2. Структура программы

Настольное объектно-ориентированное приложение на базе WPF/C# включает следующие файлы, которые представлены на рис. 16:

App.config – конфигурация программы;

App.xaml – объявление ресурсов, используемых по всему приложению;

ClassDiagram1.cd – диаграмма классов данного приложения;

Image1.png – изображение исходной фигуры;

MainWindow.xaml – разметка формы;

MainWindow.xaml.cs – описание методов и событий формы;

MonteCarlo.cs – класс MonteCarlo, реализующий вычисление площади фигуры по методу Монте-Карло;

Figure.cs – класс Figure, описывающий абстрактную фигуру;

Rectangle.cs – класса Rectangle, описывающий прямоугольник;

Triangle.cs – класса Triangle, описывающий треугольник.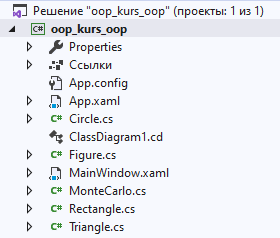



Рис. 16. Проект объектно-ориентированного приложения

5.3.3. Системные требования

Технические средства должны отвечать следующим системным требованиям приложения: 

• 
  операционная система Windows 10 и выше;
  

• 
  платформа .NET Framework 4.8 и выше;
  
• 
  архитектура 32-разрядная (х86)/64-разрядная (х64);
  
• 
  оперативная память 512 МБ и более;
  
• 
  устройства ввода: клавиатура, мышь.
  

5.3.4. Входные и выходные данные

На вход в программу поступают координаты трёх основных точек, по которым можно рассчитать координаты всех других точек фигуры. Данные заполняет пользователь вручную или из тестового примера.

На выходе пользователь получает таблицу, которая содержит несколько итераций расчёта площади фигуры, процента погрешности измерений и времени, за которое выполнен каждый расчёт. Также программа считает площадь фигуры с помощью геометрических формул.