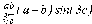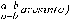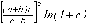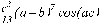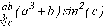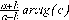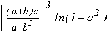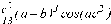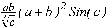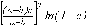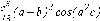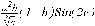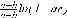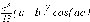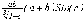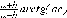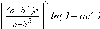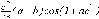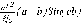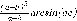Лабораторная работа по комп.математике. Вычисление предельной относительной погрешности

• Название: Вычисление предельной относительной погрешности
• Анкор: Лабораторная работа по комп.математике
• Дата: 28.09.2021
• Размер: 490.16 Kb.
• Имя файла: archivetempLaboratornaya rabota.docx
• Тип: Лабораторная работа; #238481
• страница: 1 из 4

СЕВЕРО-КАЗАХСТАНСКИЙ

ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

ИМ. М. КОЗЫБАЕВА

Ушакова Е.В.
Методические указания по выполнению лабораторных работ

по дисциплине
КОМПЬЮТЕРНАЯ МАТЕМАТИКА
для образовательной программы:

6В06104 Вычислительная техника и программное обеспечение

г. Петропавловск

2019г.

1. 
   Лабораторная работа 1
   
   1. 
      Тема:. Вычисление предельной относительной погрешности
      

Цель: Научиться производить действия над приближенными величинами, вычислять предельную относительную погрешность.

2. 
   
   
3. 
   Общие сведения:
   

Погрешности вычислительных операций

Абсолютная погрешность алгебраической суммы нескольких приближенных чисел не превышает суммы абсолютных погрешностей этих чисел. Если

u = ± x₁ ± x₂ ±...± x _n ,

то Δu = ± Δ x₁ ± Δx₂ ±...± Δx _n ,

и ⎪ Δu ⎪≤⎪ Δ x₁⎪ + ⎪Δx₂⎪ +...+⎪ Δx _n⎪.

Предельная абсолютная погрешность

Δ_u =Δ_x1 + Δ_x2 +...+Δ_{x n}. (1)

Отсюда следует, что нельзя увеличить точность суммы за счет увеличения точности отдельного слагаемого.

Правила сложения приближенных чисел:

– выделить слагаемое (слагаемые), десятичная запись которого обрывается ранее других, и оставить его без изменения;

– остальные слагаемые округлить по образцу выделенного, сохраняя один или два запасных знака;

– произвести сложение, учитывая все сохраненные знаки;

– результат округлить на один знак.

Потеря точности при вычитании близких приближенных чисел. Определим предельную относительную погрешность разности двух приближенных чисел. Пусть u = x₁ – x₂. Используя (1.7), получим

Δ_u = Δ_x1 + Δ_x2.

Предельная относительная погрешность

δ _u = Δ _u / A, (2)

где А – точное значение абсолютной величины разности u.

Если уменьшаемое и вычитаемое – близкие числа, то А будет мало и сильно увеличит предельную относительную погрешность разности.

Рассмотрим пример.

Пусть x₁ = 47,132 и x₂ = 47,111 заданы с пятью верными знаками.
Разность u = x₁ – x₂ = 0,021. Предельные абсолютные погрешности
Δ_x1 = Δ_x2 = 0,0005. Предельная абсолютная погрешность разности по (1) равна Δ_u = Δ_x1 + Δ_x2 = 0,001.

Предельные относительные погрешности:

δ _x1 = 0,0005/47,132 ≈ 0,00001;

δ _x2 = 0,0005/47,111 ≈ 0,00001;

δ _u = 0,001/0,021 ≈ 0,05.

Предельная относительная погрешность разности примерно в 5000 раз больше предельной относительной погрешности исходных данных этого примера.

Отсюда следуют правила для вычислений:

– следует по возможности избегать вычитания близких приближенных чисел;

– при необходимости такого вычитания следует уменьшаемое и вычитаемое брать с достаточным числом запасных верных знаков.

Определим предельную относительную погрешность произведения нескольких приближенных чисел. Относительная погрешность произведения нескольких приближенных чисел не превышает суммы относительных погрешностей этих чисел:

δ ≤ δ₁ + δ₂ +...+ δ _n ,

отсюда предельная относительная погрешность произведения u = x₁ x ₂...x _n следующая:

δ _u= δ _x1 + δ _x2 + ... + δ _xn, (3)

а предельная абсолютная погрешность

Δ_u = ⎪u⎪ δ _u. (4)

В частном случае умножения точного числа k на приближенное число х

u = kx,

δ _u = δ _x ,

Δ_u = ⎪ k ⎪Δ_x.

В этом частном случае относительная предельная погрешность не изменяется, а абсолютная предельная погрешность увеличивается в ⎪k⎪ раз.

Практические правила при умножении приближенных чисел:

– округлить приближенные числа так, чтобы каждое содержало на одну значащую цифру больше, чем число верных цифр в наименее точном сомножителе;

– в результате умножения сохранить столько значащих цифр, сколько верных цифр имеется в наименее точном из сомножителей.

Для частного u = x/y также верно соотношение типа (3), т.е. δ_u = δ_x + δ_y.

Если делимое и делитель имеют по меньшей мере m верных цифр, то запредельную относительную погрешность может быть принята величина

δ _u = 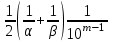, (5)

где α и β – первые значащие цифры делимого и делителя соответственно.

При возведении приближенного числа в степень m предельная относительная погрешность возрастает в m раз. При извлечении корня
m-й степени из приближенного числа предельная относительная погрешность уменьшается в m раз.

Общая формула для вычисления погрешности.

Если задана дифференцируемая функция u = f (x₁, x₂, ... x _n) и ⎪ Δx _i ⎪ (i = 1, 2, ...n) – абсолютные погрешности аргументов, то предельная погрешность функции

Δu = 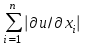Δx_i , (6)

а предельная относительная погрешность

δu = 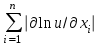Δx_i . (7)

Обратная задача теории погрешностей

На практике часто приходится решать обратную задачу – определять необходимые погрешности аргументов функции для обеспечения заданной погрешности функции. Эта задача является некорректной, так как заданную погрешность функции можно обеспечить различными сочетаниями погрешностей аргументов.

Для решения задачи принимают дополнительные условия. Одним из них является принцип равных влияний. Согласно этому принципу полагают, что все частные дифференциалы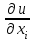

Δx _i ( i = 1, 2, ...n)

одинаково влияют на образование общей абсолютной погрешности Δ_u функции. Тогда в формуле (6) будем иметь n одинаковых слагаемых и решение задачи следующее:

Δxi = 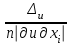; (i = 1, 2, ...n ). (8)

4. 
   
   
5. 
   Порядок выполнения лабораторной работы:
   

1. 
   Запишите порядок выполняемых вами операций, оцените погрешности их результатов, вычислите и запишите искомое значение.
   
2. 
   Выясните погрешность задания исходных данных, необходимую для получения результата с m верными значащими цифрами.
   
3. 
   Варианты заданий
   

№		F(a, b, c)	a	b	c	m
1	1		2456 ±0.0005	0.00078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	5
2	1		0.2456 ±0.0005	0.20078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	5
3	1		0.12456 ±0.0005	0.0078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	4
4	1		0.2456 ±0.0005	0.20078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	5
5	1		0.12456 ±0.0005	0.078 ±0.0003	0.2468 ±0.00013
	2		0.02456	0.007823	0.835	4
6	1		0.2456 ±0.0005	0.20078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	5
7	1		2456 ±0.0005	0.00078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	4
8	1		0.2456 ±0.0005	0.20078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	4
9	1		0.12456 ±0.0005	0.0078 ±0.00003	0.008 ±0.00013
	2		0.02456	0.007823	0.8348	4
10	1		0.2556 ±0.0005	0.50078 ±0.00003	0.8 ±0.013
	2		0.02456	0.007823	0.8348	4
11	1		0.2456 ±0.0005	0.0078 ±0.00003	8 ±1.23
	2		0.02456	0.007823	0.8348	4

6. 
   Форма отчета
   
7. 
   Отчет о проделанной работе в фале MS Word.
   

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

8. 
   
   
9. 
   Выводы
   

В результате выполнения лабораторной работы студент должен ознакомиться с теоретическим материалом по теме работы, выполнить задание по варианту, оформить отчет.

10. 
    Вопросы к защите лабораторной работы
    

1. 
   Как находится абсолютная погрешность суммы приближенных чисел?
   
2. 
   Чему равна абсолютная погрешность разности приближенных чисел?
   
3. 
   Как находится относительная погрешность суммы приближенных чисел?
   
4. 
   Как находится относительная погрешность разности приближенных чисел?
   
5. 
   Чему равна абсолютная погрешность произведения приближенных чисел?
   
6. 
   Чему равна абсолютная погрешность частного приближенных чисел?
   
7. 
   Как находится относительная погрешность произведения приближенных чисел?
   
8. 
   Как находится относительная погрешность частного приближенных чисел?
   
9. 
   В чем заключается принцип равных влияний?
   

2. 
   Лабораторная работа 2
   

Тема: Вычисление значения полинома используя схему Горнера

1. 
   Цель: Научится вычислять значение полинома с использованием схемы Горнера.
   
2. 
   Общие сведения:
   

Вычисление значений полиномов

Задан полином n-ой степени

Pn(x) = a₀ xⁿ + a₁x ^n-1 +...+a_n (2.8)

с действительными коэффициентами a_k (k = 0, 1, ...n). Требуется найти значение полинома при x = ξ, т. е. P_n(ξ).

Разделим полином на двучлен x – ξ. В общем случае получим частное в виде полинома Q_n-1(x) и остаток b_n. Можно записать:

P_n(x) = Q _n-1(x) (x- ξ) + b_n. (2.9)

По теореме Безу остаток равен значению исходного полинома при x = ξ, т. е.

P_n(ξ ) = b_n. (2.10)

Это соотношение легко получить, положив в (2.9) х = ξ. В частном случае b_n= 0 и ξ есть корень полинома, т. е. P_n (ξ) = 0.

Чтобы не производить указанного выше деления, воспользуемся схемой Горнера для определения коэффициентов b_i полинома Q _n-1 (x):

a₀ a₁ a₂ … a _n ⎣ ξ

+

b₀ξ b₁ξ … b_n-1ξ

b₀ b₁ b₂ .... b _n = P_n (ξ).

Коэффициенты вычисляются по формулам:

b₀ = a₀ + 0 ξ;

b₁ = a₁ + b₀ξ;

b₂ = a₂ + b₁ξ;

.....................

b_n = a_n + b _n-1ξ.

Имеем набор повторяющихся операций b_i = a_i+ b_i-1 ξ (i = 0, 1,…, n), который легко запрограммировать.

Вычисление значений рациональных дробей

Рациональную дробь можно представить в виде отношения двух полиномов:

R(x) = P_n(x)/ Q_m(x).

Для расчета значения R(ξ) дроби в точке x = ξ R(ξ) = P_n(ξ)/Q_m (ξ) находим значения P_n(ξ) и Q_m(ξ) по приведенной выше схеме и производим их деление.

3. 
   
   

Порядок выполнения лабораторной работы:

Задание: Вычислить значение полинома при х = ξ, используя схему Горнера.

Проверить вычисления на компьютере в системе MathCad.

Вариант	Полином	ξ
1	X4 – 2X3 + 3X2 + 4X – 1	2
2	X4 + 2X3 + 3X2 – 4X – 1	3
3	X4 – 8X3 + 5X2 + 2X – 7	2
4	3X4 – 10X3 + 22X2 – 24X + 10	2
5	X4 – X3 – 5X2 – X – 6	3
6	2X4 – 3X3 – 3X2 + 4X – 7	2
7	X4 – 8X3 + 5X2 + 2X – 7	4
8	X4 – 2X3 + 3X2 – 4X – 1	4
9	2X4 – 3X3 + 4X2 – X + 1	3
10	3X4 – 2X3 – 3X2 + 4X – 7	2

4. 
   
   
5. 
   Форма отчета: отчет о проделанной работе в фале MS Word.
   

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

6. 
   
   
7. 
   
   

Выводы: В результате выполнения лабораторной работы студент должен ознакомиться с теоретическим материалом по теме работы, выполнить задание по варианту, оформить отчет.
Вопросы к защите лабораторной работы:

1. 
   В чем состоит основная идея метода итераций?
   
2. 
   Для чего используется схема Горнера?
   
3. 
   Приведите пример вычисления значения рациональной дроби с использованием схемы Горнера.
   
4. 
   В каких случаях рационально применение схемы Горнера?
   

3. 
   Лабораторная работа 3