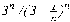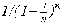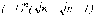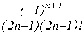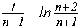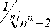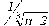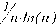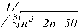Лабораторная работа по комп.математике. Вычисление предельной относительной погрешности

• Название: Вычисление предельной относительной погрешности
• Анкор: Лабораторная работа по комп.математике
• Дата: 28.09.2021
• Размер: 490.16 Kb.
• Имя файла: archivetempLaboratornaya rabota.docx
• Тип: Лабораторная работа; #238481
• страница: 2 из 4

Тема: Вычисление значения функции путём разложения функции в степенной ряд.

Цель работы: научится вычислять значение функции путём разложения ее в степенной ряд.

Задание:

Задание 1. Найдите оценки пределов последовательностей {an}, {bn}, если они существуют, с точностью e =10-2 и соответствующие порядковые номера N(e ). Изобразите графически характер поведения этих последовательностей. Найдите аналитическим путем истинное значение предела и порядок сходимости.

Задание 2. Выберите любую из приведенных последовательностей c нулевым пределом и найдите сумму соответствующего ряда при n=1, 2,... с точностью e =10-4.

Варианты заданий

№	an	bn
1		(-1)n (1-cos(1/n))
2	arctg(n2)	(-1)nn/(n2+1)
3
4		(-1)n (1-21/n)
5	arctg(n2+1)
6
7		(-1)n+1 /n2
8	ln(1+(1+n)1/n)	en⋅sin(2/n)
9	2 / ln(12n-2)
10
11	n sin(5/n)

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Какие методы изучает численная математика?
   
2. 
   Какие СКМ вам известны?
   
3. 
   Перечислите основные источники погрешностей?
   
4. 
   Дайте определение значащим цифрам?
   
5. 
   Дайте определение верным цифрам?
   
6. 
   Какая функция называется аналитической?
   
7. 
   Приведите пример вычисления значения полинома с использованием схемы Горнера.
   
8. 
   Как можно вычислять значения рациональных дробей?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   С помощью каких методов может быть решена поставленная задача?
   
2. 
   Какие известные СКМ решают такого типа задачи?
   
3. 
   Основные источники погрешностей?
   
4. 
   Как определить количество значащих цифр?
   
5. 
   Как определить количество верных цифр?
   
6. 
   Что такое М-файл?
   
7. 
   Приведите пример вычисления значения полинома с использованием СКМ Матлаб.
   
8. 
   Как можно вычислить значение рациональной дроби в Матлаб?
   

4. 
   Лабораторная работа 4
   

Тема: Вычисление значения функции с заданной точностью методом итераций.
Цель работы: научиться вычислять значения функций с заданной точностью методом итераций.

Задание:

Задание 1. Выполните обращение матрицы А и решение системы АХ=В методом Гаусса по любой из известных схем, ограничиваясь в записи чисел тремя знаками после запятой. Получите решение той же задачи в среде MatLab и сравните полученные результаты. Приняв найденное методом Гаусса решение за начальное приближение, выполните его уточнение до 4-5 знаков методом итераций. Решите численно эту задачу методом наименьших квадратов с точностью 0,001

Задание 2. Решите систему СХ=D используя команду обратного деления, методом обратной матрицы, методом Крамера. Сопоставьте полученные решения.

Варианты заданий

№1	A B 1 0.47 -0.11 0.55 .1.33 0.42 1 0.35 0.17 1.29 -0.25 0.67 1 0.36 2.11 0.54 -0.32 -0.74 1 0.10	C D 1 2 3 13 2 3 5 4 3 5 9 17
№2	0.63 1 0.11 0.34 2.08 0.17 1.18 -0.45 0.11 0.17 0.31 -0.15 1.17 -2.35 1.28 0.58 0.21 -3.45 -1.18 0.05	1 2 3 0.55 1 4 9 1.35 1 8 27 3.55
№3	0.77 0.04 -0.21 0.18 1.24 -0.45 1.23 -0.06 0 -0.88 -0.26 -0.34 1.11 0 0.62 -0.05 0.26 -0.34 1.12 -1.17	0.42 1.43 0.27 1 1.43 -0.84 0.93 2 0.27 0.93 -0.48 3
№4	0.79 -0.12 0.34 0.16 -0.64 -0.34 1.18 -0.17 0.18 1.42 -0.16 -0.34 0.85 0.31 -0.42 -0.12 0.26 0.08 0.75 0.83	0.64 0.54 -0.33 3 0.54 -0.92 0.24 2 -0.33 0.24 0.78 1
№5	-0.68 -0.18 0.02 0.21 -1.83 0.16 -0.88 -0.14 0.27 0.65 0.37 0.27 -1.02 -0.24 -2.23 0.12 0.21 -0.18 -0.75 1.13	0.5 1.77 0.39 1.5 0.84 1.79 0.95 2.5 0.24 1.03 -0.41 3
№6	-0.58 -0.32 0.03 0 -0.44 0.11 -1.26 -0.36 0 -1.42 0.12 0.08 -1.14 -0.24 0.83 0.15 -0.35 -0.18 0 1.42	0.19 0.51 0.86 0.35 0.51 0.32 0.95 0.42 0.86 0.95 -0.12 0.45
№7	-0.83 0.31 -0.18 0.22 1.71 -0.21 -0.67 0 0.22 -0.62 0.32 -0.18 -0.95 -0.19 0.89 0.12 0.28 -0.14 -1 -0.94	0.64 1.54 -0.33 0.3 1.54 -0.92 0.24 0.2 -0.33 0.24 0.78 0.1
№8	-0.87 0.27 -0.22 -0.18 -1.21 -0.21 -1 -0.45 0.18 0.33 0.12 0.13 -0.33 0.18 0.48 0.33 -0.41 0 -1 1.21	0.55 1.77 0.39 1.5 0.84 1.79 0.95 2.5 0.24 1.03 -0.41 3
№9	-0.81 -0.07 0.38 -0.21 0.81 -0.22 -0.92 0.11 0.33 0.64 0.51 -0.07 -0.81 -0.11 1.71 0.33 -0.41 0 -1 1.21	0.59 1.77 1.39 1.5 0.84 1.79 0.95 2.5 1.24 1.03 -0.41 3
№10	-1 0.22 -0.11 0.31 -2.7 0.38 -1 -0.12 0.22 1.5 0.11 0.23 1 -0.51 1.2 0.17 -0.21 0.31 -1 0.17	1.42 1.43 0.27 0.1 1.43 -0.84 0.93 0.2 0.27 0.93 -0.48 0.3
№11	-0.93 -0.08 0.11 -1.18 0.51 0.18 -0.48 0 0.21 -1.17 0.13 0.31 -1 -0.21 1.02 0.08 0 -0.33 -0.72 0.28	-0.93 -0.08 0.11 1.18 0.18 -0.48 0 0.21 0.13 0.31 -1 0.210

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Назовите этапы приближенного нахождения изолированных действительных корней уравнений.
   
2. 
   В чем состоит суть процесса отделения корней уравнения?
   
3. 
   В чем состоит суть процесса уточнения приближенных корней уравнения?
   
4. 
   Назовите методы уточнения приближенных корней.
   
5. 
   Перечислите методы отделения корней уравнений.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В чем заключается решение систем уравнений методом Крамера?
   
2. 
   Для каких матриц существуют обратные матрицы?
   
3. 
   Суть метода Гаусса.
   
4. 
   В чем основное отличие метода Жордана-Гаусса от метода Гаусса?
   
5. 
   Запишите формулы для итерационного процесса поиска решения уравнений.
   
6. 
   Запишите формулы для итерационного процесса поиска решения системы ЛАУ.
   

5. 
   Лабораторная работа 5