Лабораторная работа по комп.математике. Вычисление предельной относительной погрешности

• Название: Вычисление предельной относительной погрешности
• Анкор: Лабораторная работа по комп.математике
• Дата: 28.09.2021
• Размер: 490.16 Kb.
• Имя файла: archivetempLaboratornaya rabota.docx
• Тип: Лабораторная работа; #238481
• страница: 3 из 4

Тема: Решение уравнений методом хорд.
Цель работы: научиться вычислять корни уравнений методом хорд.

Задание:

Выполните отделение корней с использованием аналитических оценок и найдите один из корней методами дихотомии и хорд с относительной погрешностью до 0.1%.

Наряду с "ручным" решением представьте решения, получаемые стандартными средствами MatLab.

Варианты заданий

№	Выражение
1	3x4+4x3-12x2-5=0
2	2x3-9x2-60x+1=0
3	x4-x-1=0
4	2x4 - x2-10=0
5	3x4+8x3+6x2-10=0
6	x4 -18x2+5x-8=0
7	x4+4x3-12x2+1=0
8	x4 - x3-2x2+3x-3=0
9	3x4+4x3-12x2+1=0
10	3x4-8x3-18x2+2=0
11	2x4-8x3+8x2-1=0

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Назовите этапы приближенного нахождения изолированных действительных корней уравнений.
   
2. 
   В чем состоит суть процесса отделения корней уравнения?
   
3. 
   В чем состоит суть процесса уточнения приближенных корней уравнения?
   
4. 
   Назовите методы уточнения приближенных корней.
   
5. 
   Перечислите методы отделения корней уравнений.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Перечислите этапы приближенного нахождения изолированных действительных корней уравнений.
   
2. 
   Назовите методы уточнения приближенных корней.
   
3. 
   Перечислите методы отделения корней уравнений.
   
4. 
   В чем суть метода касательных?
   
5. 
   В чем заключается метод хорд?
   
6. 
   В чем заключается метод дихотомии?
   
7. 
   Какие методы аналитических оценок корней уравнений в среде Матлаб вы знаете?
   

6. 
   Лабораторная работа 6
   

Тема: Решение уравнений методом касательных
Цель работы: научиться вычислять корни уравнений методом касательных.

Задание: Вычислить с погрешностью до 0,005 корень уравнения f(x) = 0 в указанном диапазоне изменения аргумента х методом касательных.

Вариант	f(x)	Диапазон	Вариант	f(x)	Диапазон
1	x5 – x – 0,2	1	6	x2 – 5x + 6	1
2	x4-3x2+75x-1000	-15	7	x3 – 9x + 4	2
3	tg x – x	3	8	x4 + 2x – 3	0
4	x-sin x-0,25	1,1	9	sin x – 0,5x	0
5	x3+2x2 – x-1	-3	10	sin2x – 0,5x	0

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Назовите этапы приближенного нахождения изолированных действительных корней уравнений.
   
2. 
   В чем состоит суть процесса отделения корней уравнения?
   
3. 
   В чем состоит суть процесса уточнения приближенных корней уравнения?
   
4. 
   Назовите методы уточнения приближенных корней.
   
5. 
   Перечислите методы отделения корней уравнений.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В каких случаях применяется метод касательных?
   
2. 
   В чем состоит суть процесса отделения корней уравнения?
   
3. 
   В чем состоит суть процесса уточнения приближенных корней уравнения?
   
4. 
   Назовите методы уточнения приближенных корней.
   
5. 
   Перечислите методы отделения корней уравнений.
   

7. 
   Лабораторная работа 7
   

Тема: Решение уравнений методом итераций
Цель работы: научиться вычислять корни уравнений методом итераций.

Задание:

Решить уравнение из предыдущей лабораторной работы методом итераций. Решение проверить в системе Маткад.

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Запишите формулу для итерационного процесса.
   
2. 
   Приведите примеры применения метода итераций.
   
3. 
   Какая функция называется аналитической?
   
4. 
   Приведите пример вычисления значения полинома с использованием схемы Горнера.
   
5. 
   Как можно вычислять значения рациональных дробей?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Запишите формулу для итерационного процесса.
   
2. 
   Приведите примеры применения метода итераций.
   
3. 
   Что было взято за нулевое приближение?
   
4. 
   Как выглядит выражение для итерационного процесса вашего варианта?
   
5. 
   Чему равно значение первого приближения?
   
6. 
   Сколько итераций вам потребовалось для достижения требуемой точности?
   
7. 
   Сколько итераций потребовалось бы в случае, если бы вам потребовалось вычислить с точностью до 0,1?
   

8Лабораторная работа 8
Тема: Решение систем линейных алгебраических уравнений методом итераций
Цель работы: научиться вычислять корни систем линейных алгебраических уравнений методом итераций.

Задание:

Решить систему линейных алгебраических уравнений с точностью до двух знаков методом итерации.

1.	4x1 + 0,24x2 – 0,08x3 = 8; 0,09x1 +3x2 – 0,15x3 = 9; 0,04x1 – 0,08x2 + 4x3 = 20.	2.	2x1 – x2 + x3 = -3; 3x1 + 5x2 – 2x3 = 1; x1 – 4x2 + 10x3 = 0.
3.	10x1 +2x2 + x3 = 35; x1 + 5x2 + x3 = 29; 2x1 + 0,5x2 + 4x3 = 34.	4.	5x1 + x2 + 2x3 = 17; 2x1 + 7x2 – x3 = -7; x1 – 2x2 + 8x3 = 36.
5.	4x1 + x2 + x3 = 24; x1 + 3x2 + 2x3 = – 10; 2x1 + x2 + 7x3 = -28.	6.	5x1 + 2x2 x3 = 19; x1 + 4x2 + 2x3 = 11; 2x1 + 3x2 + 6x3 = 21.
7.	7x1 + 5x2 + 2x3 = 48; 2x1 + 10x2 – x3 = 27; x1 + 2x2 – 3x3 = 18.	8.	2x1 + 0,5x2 + 0,5x3 = 12; x1 + 3x2 + x3 = -4; 3x1 + 2x2 – 8x3 = 68.
9.	10x1 + 2x2 + x3 = 32; x1 + 5x2 + x3 = 47; 2x1 + 0,5x2 + 4x3 = 30.	10.	4x1 – x2 –2x3 = 15; 3x1 + 6x2 – x3 = 19; x1 + 2x2 + 3x3 = 13.

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Запишите формулу для итерационного процесса.
   
2. 
   Приведите примеры применения метода итераций.
   
3. 
   Какая функция называется аналитической?
   
4. 
   Приведите пример вычисления значения полинома с использованием схемы Горнера.
   
5. 
   Как можно вычислять значения рациональных дробей?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Запишите формулу для итерационного процесса.
   
2. 
   Приведите примеры применения метода итераций.
   
3. 
   Что было взято за нулевое приближение?
   
4. 
   Как выглядит выражение для итерационного процесса вашего варианта?
   
5. 
   Чему равно значение первого приближения?
   
6. 
   Сколько итераций вам потребовалось для достижения требуемой точности?
   
7. 
   Сколько итераций потребовалось бы в случае, если бы вам потребовалось вычислить с точностью до 0,1?
   

9. Лабораторная работа 9
Тема: Решение систем линейных алгебраических уравнений методом Крамера
Цель работы: научиться вычислять корни систем линейных алгебраических уравнений методом Крамера.

Задание:

Решить систему линейных алгебраических уравнений с помощью формул Крамера.

1.	4x1 + 0,24x2 – 0,08x3 = 8; 0,09x1 +3x2 – 0,15x3 = 9; 0,04x1 – 0,08x2 + 4x3 = 20.	2.	2x1 – x2 + x3 = -3; 3x1 + 5x2 – 2x3 = 1; x1 – 4x2 + 10x3 = 0.
3.	10x1 +2x2 + x3 = 35; x1 + 5x2 + x3 = 29; 2x1 + 0,5x2 + 4x3 = 34.	4.	5x1 + x2 + 2x3 = 17; 2x1 + 7x2 – x3 = -7; x1 – 2x2 + 8x3 = 36.
5.	4x1 + x2 + x3 = 24; x1 + 3x2 + 2x3 = – 10; 2x1 + x2 + 7x3 = -28.	6.	5x1 + 2x2 x3 = 19; x1 + 4x2 + 2x3 = 11; 2x1 + 3x2 + 6x3 = 21.
7.	7x1 + 5x2 + 2x3 = 48; 2x1 + 10x2 – x3 = 27; x1 + 2x2 – 3x3 = 18.	8.	2x1 + 0,5x2 + 0,5x3 = 12; x1 + 3x2 + x3 = -4; 3x1 + 2x2 – 8x3 = 68.
9.	10x1 + 2x2 + x3 = 32; x1 + 5x2 + x3 = 47; 2x1 + 0,5x2 + 4x3 = 30.	10.	4x1 – x2 –2x3 = 15; 3x1 + 6x2 – x3 = 19; x1 + 2x2 + 3x3 = 13.

Вопросы для допуска к выполнению лабораторной работы:

1. 
   В чем заключается решение систем уравнений методом Крамера?
   
2. 
   Для каких матриц существуют обратные матрицы?
   
3. 
   Суть метода Гаусса.
   
4. 
   В чем основное отличие метода Жордана-Гаусса от метода Гаусса?
   
5. 
   Запишите формулы для итерационного процесса поиска решения системы ЛАУ.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В каких случаях возможно решение систем уравнений методом Крамера?
   
2. 
   В каких случаях нельзя пользоваться формулами Крамера?
   
3. 
   Укажите соотношения для вычисления корней системы линейных уравнений по методу Крамера.
   
4. 
   С помощью какой функции в Матлаб можно вычислить определитель матрицы?
   
5. 
   С помощью какой функции в Матлаб можно ввести матрицу?
   

10.Лабораторная работа 10
Тема: Решение систем линейных алгебраических уравнений
Цель работы: научиться вычислять корни систме линейных алгебраических уравнений в среде Матлаб.

Задание:

Решить задания к предыдущим 2-м лабораторным работам с помощью системы Матлаб.

Теоретические сведения

Формулы Крамера

Дана система n ЛАУ:

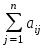x_j = b_i; (i = 1, 2, ...n). (4.1)

Образуем матрицу коэффициентов системы и векторы-колонки (векторы-столбцы) неизвестных и свободных членов:

A = [a_ij ], x = [x_j ], b = [b_i].

Матричная запись (4.1) имеет вид:

Ax = b. (4.2)

Если матрица А – неособенная (detA = Δ ≠ 0), то существует обратная матрица А^-1. Умножая обе части равенства (4.2) слева на обратнуюматрицу, получим

А^-1А х = А^-1 b или х = А^-1 b. (4.3)

Формула (4.3) дает решение задачи. Для вычисления корней по (4.3) нужно уметь обращать матрицы и производить их умножение.

Выражая обратную матрицу через союзную матрицу А (А^-1 = А/ Δ), преобразуем (4.3) к виду:

x = A b,

или x_i= Δ _i / Δ,

где Δ _i= 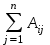A_ji b_j.

A_jI – алгебраическое дополнение элемента a_ji матрицы А.

Дополнительные детерминанты Δ i получаются из Δ путем замены i-й колонки колонкой свободных членов.

Получаем известные формулы Крамера:

x₁ = Δ₁ / Δ, x₂ = Δ₂ / Δ,... , x _n = Δ _n / Δ. (4.4)

Метод Гаусса

Пример 4.2.

Решим систему (4.5), используя метод Гаусса.

Выразим х1 из первого уравнения и подставим результат во второе и третье уравнения. Получим после простых преобразований:

2x1 + 3x2 +4x3 =15;

0 - x2/2 + 3x3 = 17/2;

0 - 13x2/2 – 5x3 = – 43/2.

Выразим из второго уравнения последней системы х2 и подставим в третье уравнение. После простых преобразований получим:

2х1 +3х2 +4х3 = 15;

0 – х2/2 +3х3 = 17/2;

0 + 0- 44x3 = – 132.

Из последнего уравнения находим х3 = 3, подставляя этот результат в предыдущее уравнение, найдем х2 =1 и из первого уравнения получим х1 = 0. Результат совпадает с (4.6).

Метод Жордана–Гаусса

Пример 4.3.

В результате описанных преобразований системе (4.5) можно придать вид:

1*x1 + 0*x2 + 0*x3 = 0;

0*x1 + 1*x2 + 0*x3 = 1;

0*x1 + 0*x2 + 1*x3 = 3;

откуда видно, что x1 = 0; x2 = 1; x3 = 3.

Метод итераций

Пример 4.4.

Рассмотрим решение следующей системы ЛАУ:

10x1 + x2 + 2x3 = 7;

x1 + 5x2 +x3 = 8; (4.8)

 3x1 – 2x2 +6x3 = 16.

Преобразуем ее к виду:

x1 = 0,7 – 0,1x2 – 0,2x3;

x2 = 1,6 – 0,2x1 – 0,2x2; (4.9)

x3 = 2,67 – 0,5x1 + 0,33x2.

За нулевое приближение корней примем значения:

x1⁽⁰⁾ = 0,7; x2⁽⁰⁾ = 1,6; x3⁽⁰⁾ = 2,67.

Рассчитываем первое приближение для корней, используя в (4.9) предыдущее приближение:

x1⁽¹⁾ = 0,7 – 0,1*1,6 – 0,2*2,67 = 0,006;

x2⁽¹⁾ = 1,6 – 0,2*0,7 -0,2*1,6 = 1,264;

x3⁽¹⁾ = 2,67 – 0,5*0,7 + 0,33*2,67 = 3,20.

Второе и последующие приближения рассчитываются аналогично. Уже первое приближение дает результаты, близкие к точным значениям корней.

Вопросы для допуска к выполнению лабораторной работы:

1. 
   В чем заключается решение систем уравнений методом Крамера?
   
2. 
   Для каких матриц существуют обратные матрицы?
   
3. 
   Суть метода Гаусса.
   
4. 
   В чем основное отличие метода Жордана-Гаусса от метода Гаусса?
   
5. 
   Запишите формулы для итерационного процесса поиска решения системы ЛАУ.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Что значит решить СЛАУ?
   
2. 
   Какой метод решения СЛАУ Вы выбрали?
   
3. 
   Почему был выбран именно этот метод решения СЛАУ?
   
4. 
   В чем основное отличие метода Жордана-Гаусса от метода Гаусса?
   
5. 
   Запишите формулы для итерационного процесса поиска решения системы Вашей СЛАУ.
   

11.Лабораторная работа 11