Лабораторная работа по комп.математике. Вычисление предельной относительной погрешности

• Название: Вычисление предельной относительной погрешности
• Анкор: Лабораторная работа по комп.математике
• Дата: 28.09.2021
• Размер: 490.16 Kb.
• Имя файла: archivetempLaboratornaya rabota.docx
• Тип: Лабораторная работа; #238481
• страница: 4 из 4

Тема: Интерполирование. Интерполяционные формулы.
Цель работы: научиться применять интерполяционные формулы для заданной совокупности данных.

Задание:

Подобрать интерполяционный полином по формуле Лагранжа для следующей совокупности данных x_i, y_i. Выполнить эту задачу также в системе Матлаб.

Вариант	xi	1	2	3	4	5
1	yi	0,7	1,9	1,1	2,2	3,5
2	yi	0,8	2,4	1,5	2,3	4,0
3	yi	2,1	3,0	1,5	3,2	4,1
4	yi	2,2	4,8	1,9	3,9	5,5
5	yi	1,0	3,5	5,0	5,6	3,8
6	yi	2,6	1,1	1,6	3,2	2,4
7	yi	3,5	4,8	3,5	1,8	1,5
8	yi	6,0	3,2	1,9	1,3	1,2
9	yi	1,5	1,8	2,5	4,0	7,0
10	yi	0	6,0	2,0	1,3	6,0

Вопросы для допуска к выполнению лабораторной работы:

1. 
   В чем заключается практическое назначение задачи интерполирования функций?
   
2. 
   Какая функция называется интерполирующей?
   
3. 
   Дайте понятие конечным разностям.
   
4. 
   Какие интерполяционные формулы используются при равноотстоящих узлах?
   
5. 
   Какие интерполяционные формулы используются при произвольных узлах?
   
6. 
   В чем заключается интерполяция сплайнами?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В каких случаях ставится задача интерполирования функций?
   
2. 
   Какая функция использована Вами в качестве интерполирующей?
   
3. 
   Какой формулой Вы пользовались для интерполирования?
   
4. 
   Какие узлы интерполирования даны в Вашем случае (равноотстоящие или произвольные)?
   
5. 
   Какие интерполяционные формулы используются при произвольных узлах?
   
6. 
   Наибольшее применение на практике нашел случай интерполяции сплайнами какой степени?
   
7. 
   В чем заключается кусочная интерполяция?
   

12.Лабораторная работа 12
Тема: Линейная регрессия.
Цель работы: научиться подбирать линейную регрессию для заданной совокупности данных.

Задание:

Подобрать линейную регрессию для данных предыдущей задачи. Результат проверить в системе Матлаб.

Теоретические сведения

При большом числе точек исходных данных решение задачи интерполяции значительно усложняется вследствие роста степени интерполяционного полинома. С учетом неизбежных погрешностей исходных данных при подборе заменяющей их кривой можно снять требование обязательного прохождения этой кривой через заданные точки, заменив его требованием достаточной близости кривой к точкам.

Тогда задачу можно сформулировать следующим образом: для «облака» точек xi , yi (i =1, 2, ...n) подобрать кривую y(x), которая давала бы значения y(xi), достаточно близкие к yi.

Кривая y(x) называется аппроксимирующей кривой или линией регрессии. Для единственности решения нужно, как и при интерполяции, оговорить класс аппроксимирующей кривой и, кроме того, критерий ее близости к точкам исходных данных. В методе наименьших квадратов таким критерием является минимум суммы квадратов отклонений ординат y(xi) линии регрессии от ординат yi экспериментальных точек. Эта сумма имеет вид:

S = 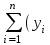– y(x _i))². (6.1)

В качестве класса аппроксимирующей функции часто выбираются степенные полиномы

y(x) = a0 + a1 x + a2 x2 +...+ am xm ; ( m < n ). (6.2)

Вопросы для допуска к выполнению лабораторной работы:

1. 
   В каком случае возникает необходимость постановки задачи аппроксимации?
   
2. 
   Сформулируйте задачу аппроксимации функции?
   
3. 
   Какая кривая называется линией регрессии?
   
4. 
   Для чего используется метод наименьших квадратов?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   В чем заключается задача аппроксимации?
   
2. 
   Для чего используется аппроксимация функции на практике?
   
3. 
   В каком виде Вы искали линию регрессии?
   
4. 
   Для чего используется метод наименьших квадратов?
   
5. 
   Что называется аппроксимирующей кривой?
   

13. 
    Лабораторная работа 13
    

Тема: Численное интегрирование функции.
Цель работы: научиться выполнять численное интегрирование заданной функции.

Задание:

Выполнить численное интегрирование заданной функции f(x) в заданных пределах a, b. Использовать метод по выбору. Проверить решение в системе Матлаб.

Вариант	f(x)	a	b
1	(4x – x2)	0	2
2	4/(1 + x2)	0	1
3	sin x/ x	0	1
4	(1 – x2)0,5	-1	1
5	sin2x/(1 + x5)	0	3
6	sin4x exp(-2x)	0	3
7	1/x0,5	0,04	1
8	1/(x2 + 0,1	0	2
9	sin(1/x)	1/2π	2
10	exp(x2/2)	0	1

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Сформулируйте задачу численного интегрирования?
   
2. 
   Запишите простейшие квадратурные формулы.
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Какой метод численного интегрирования Вы выбрали? Почему?
   
2. 
   Запишите простейшие квадратурные формулы. Приведите примеры их использования.
   

13. 
    Лабораторная работа 14
    

Тема: Решение ОДУ.
Цель работы: научиться решать ОДУ в системе Матлаб.

Задание:

Решить численно обыкновенное дифференциальное уравнение при указанных начальных условиях и значении аргумента х. Метод решения – по выбору. Проверить решение в системе Матлаб.

Вариант	Уравнение	Начальные условия	х
1	y'' + 4y = exp (-2x)	y(0) = y' (0) = 0	1
2	y'' + 5y' + 6y = 12cos2x	y(0) = 1, y' (0) = 3	2
3	y'' + 4y' –12y = 8sin2x	y(0) = y' (0) = 0	1
4	y'' – 6y' + 9y = x^2 – x + 3	y(0) = 4/3, y'(0) = 1/27	1
5	y'' – 2y' + 5y =x exp(2x)	y(0) = 1, y'(0) = 0	3
6	y'' – 5y' + 6y = (12x – 7) exp(-x)	y(0) = y' (0) = 0	2
7	y'' – 4y' + 13y =26x + 5	y(0) = 1, y'(0) = 0	1
8	y'' – 4y' = 6x^2 +1	y(0) = 2, y'(0) = 3	3
9	y'' – 2y' + y = 16exp(x)	y(0) = 1, y'(0) = 2	2
10	y'' + 6y + 9y = 10exp(-3x)	y(0) = 3, y'(0) = 2	1

Вопросы для допуска к выполнению лабораторной работы:

1. 
   Охарактеризуйте некоторые простые численные методы решения ОДУ?
   
2. 
   В чем заключается основная идея метода Эйлера?
   
3. 
   В каких случаях используется метод Рунге-Кутты?
   
4. 
   На какой идее основаны методы прогноза Адамса–Башфорда и прогноза-коррекции Адамса–Башфорда–Моултона?
   

Содержание отчета:

1. Титульный лист.

2. Цель лабораторной работы.

3. Исходные данные, указываемые в задании и необходимые для достижения поставленной цели.

4. Расчетная часть: описание выполнения задания.

5. Выводы и анализ полученных результатов.

Контрольные вопросы:

1. 
   Охарактеризуйте численные методы решения ОДУ, которые были использованы в процессе решения поставленной задачи?
   
2. 
   В чем заключается их основная идея?
   
3. 
   С помощью каких функций Матлаб они реализуются?