Лабораторная работа №2(тест). Исследование временных характеристик типовых динамических звеньев
 Скачать 1.73 Mb. Скачать 1.73 Mb.
|
                      Псковский государственный университет Псковский государственный университетОтчёт по лабораторной работе №2 «Исследование временных характеристик типовых динамических звеньев» Выполнили: Васильева А. Фёдоров Ю.И. Студенты группы 0022-02 Преподаватель: Тимошевская О.Ю. 2018 год Цели работы. С помощью интегрирующих линейных звеньев исследовать временные характеристики:
Теоретическая часть. Знакомство с приёмами исследования временных характеристик типовых звеньев удобно начинать, используя в качестве объекта исследования сменный блок «интегратор». 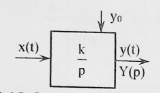 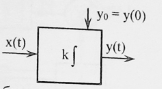 Варианты обозначения преобразователя интегрирования. Варианты обозначения преобразователя интегрирования.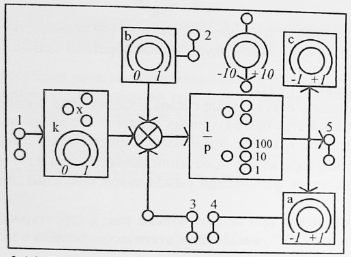 Мнемосхема передней панели сменного блока «интегратор». Мнемосхема передней панели сменного блока «интегратор».Блок k позволяет регулировать коэффициент передачи сигнала от 0 до 1 или от 0 до 10 в зависимости от установки перемычки между левым и одним из двух правых гнёзд. Выходной сигнал блока k можно суммировать с сигналами, подаваемыми на выходы 2 и 3. Коэффициент b можно плавно регулировать от 0 до 1. Выход сумматора соединён с входом преобразователя «интегратор». Установка перемычки между гнёздами 1в «интеграторе» превращает этот блок в повторитель сигнала. Установка перемычки между нижним левым гнездом и одним из трёх правых задаёт временной масштаб интегратора 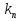 .Верхнее гнездо соединяет с перемычкой с выходом задатчика начального условия. Выход интегратора соединён с гнёздами 5 и входами коэффициентов а и с, каждый из которых можно плавно регулировать от -1 до +1. Выходные гнёзда 4коэффициентаа расположены так чтобы их было удобно соединить стандартной перемычкой с входными гнёздами 3 сумматора. .Верхнее гнездо соединяет с перемычкой с выходом задатчика начального условия. Выход интегратора соединён с гнёздами 5 и входами коэффициентов а и с, каждый из которых можно плавно регулировать от -1 до +1. Выходные гнёзда 4коэффициентаа расположены так чтобы их было удобно соединить стандартной перемычкой с входными гнёздами 3 сумматора.Переходная функция звена представляет собой реакцию звена на единичное ступенчатое воздействие при нулевых начальных условиях. Обозначение: 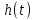 . .Импульсная переходная функция (весовая функция) описывает реакцию звена на единичное импульсное воздействие при нулевых начальных условиях. Обозначение: 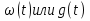 . .Единичное импульсное воздействие – дельта-функция 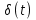 . .Между переходной и весовой функциями существует однозначная связь: 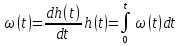 По переходной и весовой функции можно однозначно определить выходную величину при произвольном входном воздействии с помощью теоремы о свертке: 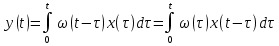 Переходная и весовая функция связаны с передаточной функцией звена 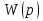 с помощью прямого преобразования Лапласа: с помощью прямого преобразования Лапласа: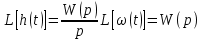 Под элементарным динамическим звеном понимают такое звено, переходный процесс в котором описывается линейным дифференциальным уравнением не выше 2-го порядка. Оборудование. АВК-6:
Эксперимент. Структурная схема исследования типового звена: 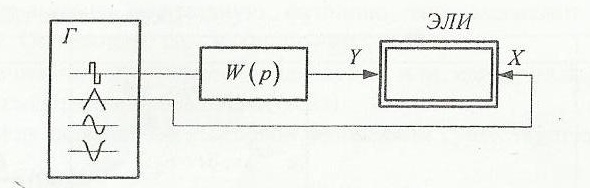
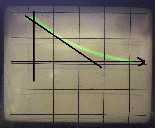
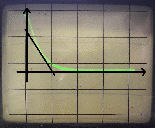
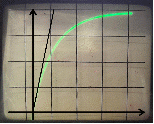
Структурная схема интегрирующего звена и примерный вид временной характеристики представлены ниже на рис.1.1 и рис.1.2 соответственно:  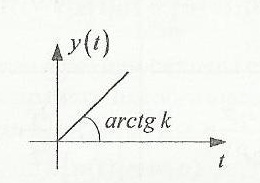
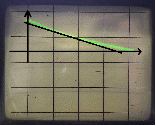
Для данного звена исследуем влияние коэффициентов настройки k и kи на характер переходного процесса. Плавно изменяя коэффициенты, зафиксируем несколько характеристик. Для различных значений коэффициентов k и kи = 1/р отобразим полученные характеристики и рассчитаем углы наклона характеристик:
Вывод: с увеличением k угол наклона характеристики увеличивается.
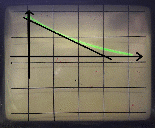
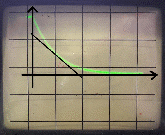
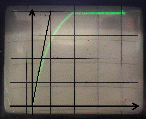
Структурная схема апериодического звена и примерный вид её характеристики представлены ниже на рис.2.1 и рис.2.2 соответственно: 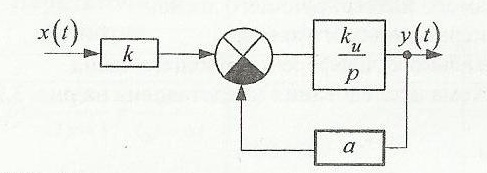 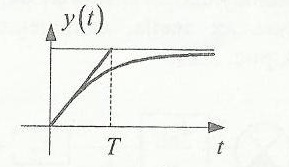
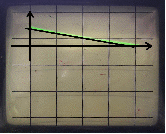
Исследуем влияние коэффициентов k и kи и полярности обратной связи на вид переходного процесса. Определим, при каких условиях апериодическое звено будет работать, как интегрирующее.Отобразим полученные характеристики и рассчитаем углы наклона характеристик с помощью проведения касательных прямых:
Вывод:апериодическоезвеноработает в качестве интегрирующего при а –> 0, также близкий к интегрирующему звену вид график будет иметь при большихkи. С увеличением коэффициента k, угол наклона характеристики увеличивается.При а>0 меняется полярностьобратной связи.
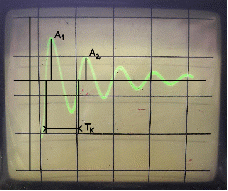
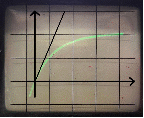
Структурная схема реального дифференцирующего звена и примерный вид её характеристики представлены ниже на рис.3.1 и рис.3.2 соответственно: 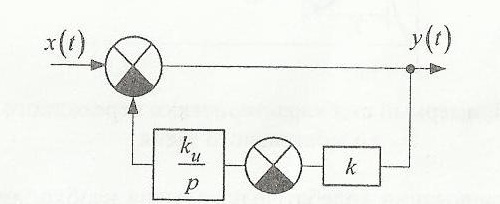 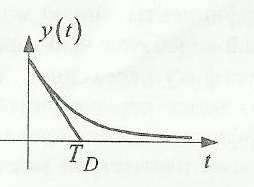
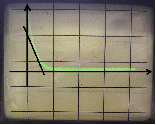
Исследуем влияние коэффициентов k и kи на вид переходного процесса. Для полученных характеристик данного звена определимпо известным параметрам настройки и по кривой переходного процесса, как изменяется значение постоянной времени дифференцирования. Вывод: при увеличении коэффициента k уменьшается значение постоянной времени дифференцирования TD.
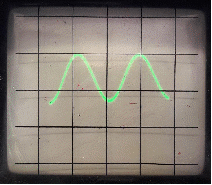
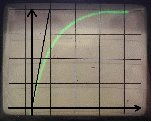
Структурная схема колебательного звена представлена ниже на рис.4.1 и рис.4.2 соответственно: 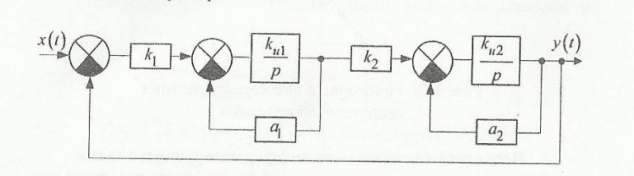 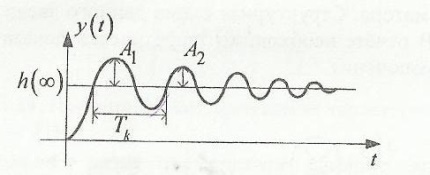
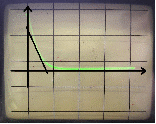
По полученному графику переходного процесса определим параметры колебательного звена(k – передаточный коэффициент, Т – постоянную времени, ξ –коэффициент демпфирования), используя соотношения: 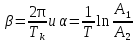 , где , где 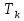 - период колебаний, - период колебаний, 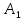 и и 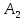 - амплитуды двух соседних колебаний относительно установившегося значения. - амплитуды двух соседних колебаний относительно установившегося значения.А1= 7,2мм А2= 3,2мм 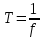 = = 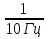 = 0,1с = 0,1сТk = (0,1c*6,4мм)/36,8мм=0,017с 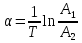 = = 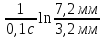 = 8,11c-1 = 8,11c-1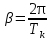 = =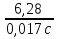 = 369,41c-1 = 369,41c-1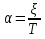 =>ξ = =>ξ = 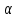 ·T = 8,11c-1·0,1с = 0,811 ·T = 8,11c-1·0,1с = 0,811Вывод: при а=+1 характеристика приняла вид гармонических колебаний; при уменьшении коэффициентов k1и k2 характеристика приняла вид апериодического звена. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
