ПОДЗЕМНАЯ ГИДРОГАЗОДИНАМИКА. Исследование взаимодействия скважин кольцевой батареи
 Скачать 229.49 Kb. Скачать 229.49 Kb.
|
|
КУРСОВАЯ РАБОТА ПО ДИСЦИПЛИНЕ «ПОДЗЕМНАЯ ГИДРОГАЗОДИНАМИКА» НА ТЕМУ: «ИССЛЕДОВАНИЕ ВЗАИМОДЕЙСТВИЯ СКВАЖИН КОЛЬЦЕВОЙ БАТАРЕИ» Вариант №31 СОДЕРЖАНИЕ Приток к прямолинейной батареи скважин 14 Полученные данные позволяют решать задачи прогнозирования и контроля разработки нефтяных, газовых, нефтегазовых и газоконденсатных пластов. Кроме того, в решении учитываются характер неоднородности пласта, характер несовершенства скважины. 1. Теоретическая часть Нефть и природные газы заключены в недрах Земли. Их скопления связаны с вмещающими горными породами - пористыми и проницаемыми образованиями, имеющими непроницаемые кровлю и подошву. Горные породы, которые могут служить вместилищами нефти и газа и отдавать их при разработке, называются породами-коллекторами. В свою очередь, коллекторы называют пористыми или трещиноватыми в зависимости от геометрии пустот. Природные жидкости (нефть, газ, подземные воды и их смеси) находятся в пустотах (порах и трещинах) коллекторов. Часто находящиеся в пустотном пространстве пласта природные жидкости обозначают общим термином флюид, подразумевая под ним любую из них. Флюид, находящийся в коллекторе, может находиться в состоянии покоя или двигаться. Движение флюидов через твердые (вообще говоря, деформируемые) трещиноватые или пористые среды называется фильтрацией. Фильтрация может быть обусловлена воздействием различных сил: градиентом давления, концентрации, температуры, капиллярными, электромолекулярными и другими силами.Например, движение (фильтрация) расплавленного жира в фитиле свечи или керосина в фитиле керосиновой лампы обусловлено капиллярными силами. Однако в дальнейшем будем рассматривать течения, вызываемые действием градиента давления или силы тяжести. Поровое пространство осадочных горных пород - сложная система сообщающихся межзернистых пустот, в которой трудно выделить отдельные поровые каналы (рисунок 1). Размеры пор, например, в песчаных породах составляют обычно единицы или десятки микрометров (мкм). Движение флюидов в пласте происходит с очень малыми скоростями, порядка микрометров в секунду (в гидромеханике движения со столь малыми скоростями часто называются ползущими).  Рисунок 1 - Шлиф нефтяного песчаника Поэтому процесс фильтрации с высокой степенью точности можно очень часто считать изотермическим. И в то же время при фильтрации в горных породах возникает значительная сила трения. При движении флюидов в пустотном пространстве коллектора соприкосновение между твердым скелетом и жидкостью происходит по огромной поверхности. Например, в 1м3 пористой среды (песчаника) площадь поверхности пустотного пространства может достигать порядка 104 м2. Поэтому основным свойством флюида, которое влияет на фильтрацию, является вязкость. В связи с этим обстоятельством вязкость учитывается даже при фильтрации газа, а так как сила трения распределена по всему объему коллектора, то Н.Е. Жуковский предложил при описании фильтрации силу трения считать массовой силой. Строение нефтяных и газовых залежей осложняется значительной неоднородностью и анизотропией свойств пород, их слоистостью, наличием тектонических и стратиграфических нарушений (разрывов сплошности породы). Разведка месторождений, исследование пластов, извлечение нефти и газа осуществляется через отдельные скважины диаметром 10-20 см, отстоящие друг от друга до сотни метров. Строение нефтяных и газовых залежей осложняется значительной неоднородностью пород, их слоистостью, наличием тектонических и стратиграфических нарушений (разрывов сплошности породы). Разведка месторождений, исследование пластов, извлечение нефти и газа осуществляются через отдельные скважины диаметром 10-20 см, отстоящие друг от друга на сотни, а иногда и тысячи метров. Теорию фильтрации нефти и газа в природных пластах характеризуют следующие особенности. 1. Невозможность изучать движение флюидов в пластах прямым применением обычных методов гидродинамики, т. е. решением уравнений движения вязкой жидкости для области, представляющей собой совокупность всех пор. 2. Сочетание очень разных масштабов фильтрационных процессов, определяемых различными характерными размерами, отличающимися по величине на многие порядки: размер пор (единицы и десятки микрометров), диаметр скважин (десятки сантиметров), расстояние между скважинами (сотни метров), протяженность месторождений (десятки километров). Масштаб неоднородности пластов вдоль и поперек их простирания может иметь практически любые значения. 3. Ограниченность и неточность сведений о строении и свойствах пласта и пластовых флюидов, не позволяющих построить однозначную модель пластовой залежи. Эти особенности приводят к формулировке основных модельных представлений и разработке методов подземной гидромеханики, направленных, прежде всего, на установление качественных закономерностей процессов и на создание расчетных схем, мало чувствительных к точности исходных данных. При этом познавательная и практическая ценность получаемых результатов в значительной степени определяется четкостью постановки расчетной задачи и глубиной предварительного анализа имеющихся данных. 2. Расчетная часть Постановка задачи: Имеется кольцевая батарея, состоящая из равнодебитных скважин, расположенная в пласте с круговым контуром питания. Исследовать эффект взаимодействия скважин в зависимости: а) от изменения числа в батарее при неизменном радиусе батареи; б) от изменения радиуса батареи при постоянном числе скважин в батарее. Исходные данные: 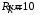 , , 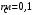 ; ;а) Rб=200 м; n=3;4;8;12;16;20;40; ∞; б) n=8; Rб=100 м; 200 м; 400 м; 600 м; 800 м; 1000 м. Методические указания: Вывести формулу для дебита скважины кольцевой батареи. Результаты расчетов представить в виде таблиц и графиков зависимостей 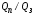 от n и Rб, где от n и Rб, где 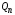 - суммарный дебит батареи, состоящей из n скважин, - суммарный дебит батареи, состоящей из n скважин, 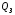 - суммарный дебит батареи, состоящей из 3-х скважин. - суммарный дебит батареи, состоящей из 3-х скважин.На примере притока жидкости к нескольким рядам или кольцевым батареям скважин можно ознакомиться с широко применяемые при проектировании разработки нефтяных месторождений методом эквивалентных фильтрационных сопротивлений, предложенным Борисовым и основанным на аналогии движения жидкости в пористой среде с течением электрического тока в проводниках. Рассмотрим задачу о притоке жидкости к одной бесконечной цепочке скважин, расположенных на расстояниях 2σ друг от друга и на расстоянии L от прямолинейного контура питания. При этом условимся, что на контуре питания будет постоянный потенциал Фк, а на забоях скважин - Фс. Определим дебит каждой скважины и суммарный дебит n скважин в цепочке. Таким образом, цепочка скважин-стоков отображается зеркально относительно контура питания в скважины-источники, и рассматривается интерференция двух цепочек скважин в неограниченном пласте. Данная задача решается методом суперпозиции. Результаты решения показывают, что на расстоянии от контура до половины расстояния между скважинами движение жидкости практически прямолинейное и падение потенциала на этом участке происходит по закону прямолинейной фильтрации. Основное падение потенциала происходит вблизи скважины, где характер движения близок к радиальному. При этом дебит каждой скважины цепочки выражается следующей формулой: 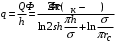 , (1) , (1)где 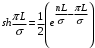 - гиперболический синус. - гиперболический синус.В случае, когда L > σ величина 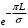 очень мала и тогда очень мала и тогда 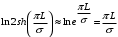 . .Отсюда следует, что при L > σ дебит скважины определяется следующим образом: 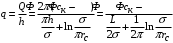 , (2) , (2)Введем обозначения 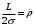 , , 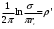 , формулу (1) представим в виде, аналогичном закону Ома. , формулу (1) представим в виде, аналогичном закону Ома.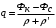 (3) (3)Величина 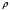 по терминологии Ю.П. Борисова, называется внешним фильтрационным сопротивлением батареи, по терминологии Ю.П. Борисова, называется внешним фильтрационным сопротивлением батареи, 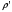 - внутренним. Таким образом, приток жидкости к цепочке скважин можно представить схемой эквивалентных фильтрационных сопротивлений. - внутренним. Таким образом, приток жидкости к цепочке скважин можно представить схемой эквивалентных фильтрационных сопротивлений.Аналогом объемного расхода q служит сила тока, а аналогом разности фильтрационных потенциалов – разность электрических потенциалов. Суммарный дебит прямолинейной цепочки из n скважин 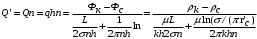 , (4) , (4)Из формулы (5.24) следует выражение для внешнего фильтрационного сопротивления цепочки: 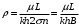 , которое представляет собой сопротивление потоку жидкости от контура питания до галереи длиной , которое представляет собой сопротивление потоку жидкости от контура питания до галереи длиной 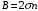 , расположенной на расстоянии L от контура питания, а внутреннее сопротивление , расположенной на расстоянии L от контура питания, а внутреннее сопротивление 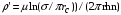 выражает сопротивление, возникающее при подходе жидкости к скважинам в зоне радиусом выражает сопротивление, возникающее при подходе жидкости к скважинам в зоне радиусом 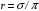 , где фильтрация практически плоскорадиальная. , где фильтрация практически плоскорадиальная.Приток жидкости к скважине в пласте вблизи прямолинейной непроницаемой границы; Приток жидкости к скважине, эксцентрично расположенной в круговом пласте – самостоятельно. Рассмотрим многорядные батареи скважин. Решение задачи об интерференции скважин в пласте с удаленным контуром питания показывает, что в общем случае приходится решать столько уравнений, сколько имеется скважин. Следовательно, для получения точного решения необходимо использование ЭВМ, т.к. на месторождениях имеется десятки и сотни скважин, но можно воспользоваться с достаточной для практики точностью приближенным решением данной задачи. При рациональной системе разработки скважины располагают обычно в виде рядов, расставленных вдоль контура нефте-газоносности и контура питания. Эти линии называются батареями или рядами скважин. Без большой погрешности можно считать дебит скважин в каждом ряду одинаковым, если в каждом ряду скважины находятся в одинаковых условиях. Дебиты же скважин в разных рядах будут отличаться друг от друга. Наибольший дебит имеет первый ряд, ближайший к контуру питания, а по мере удаления дебит уменьшается. Поэтому число одновременно работающих рядов редко превышает двух-трёх и последующие ряды включаются по мере приближения контура нефте-газоносности. Когда вода подошла к первому ряду, то он выключается и включается один из следующих рядов и т.д. В этом случае число неизвестных уменьшается от числа скважин n до числа рядов N (обычно число рядов не превышает 2-4), а это уже гораздо более простая задача. Приток к скважинам кольцевой батареи Пусть центры скважин располагаются в вершинах правильного n-угольника, т.к. что скважины образуют кольцевую батарею радиуса а (рис. 8). Контур питания удалён от скважин на расстояние, значительно превышающее радиус батареи и тогда можно считать, что все скважины равноудалены от контура питания на расстояние rк. Будем считать, что на контуре питания поддерживается постоянное значение потенциала к и на контуре скважин потенциал постоянен и равен с. В данной постановке следовательно надо решить задачу о плоском течении к n точечным стокам, размещённым равномерно на окружности радиуса а. Для получения формулы дебита скважин воспользуемся формулой (5) 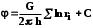 , (5) , (5)где G - массовый дебит любой скважины батареи, rj - расстояния от некоторой точки пласта до всех n скважин; h - толщина пласта. Граничные условия: на контуре питания =к=const при rj=rк; на контуре скважины =с=const при r1=rс; rj(j1)=2a sin[(n-1)/n]. Используя данные граничные условия преобразуем формулу (5) 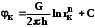 , (6) , (6)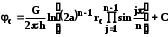 , (7) , (7)В последнем выражении 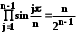 , (8) , (8)Тогда (6) перепишется в виде 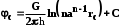 , (9) , (9)и из (5), (7) получим выражение для определения дебита скважины 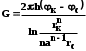 , (10) , (10)Формула (10) справедлива при любом целом n. В частности, при n=1 имеем выражение типа формулы Дюпюи для определения дебита при плоскорадиальном потоке: 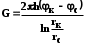 , (11) , (11)Формула (10) - приближенная. Её можно применять в случае, если размеры пласта во много раз больше площади внутри окружности батареи скважин, например, при водонапорном режиме, когда жидкость можно считать несжимаемой. Если же в пласте установился режим растворенного газа, то трудно ожидать, что площадь, занятая газированной жидкостью, простирается до границ пласта. Если расстояние до контура незначительно превышает радиус батареи, то, строго говоря, следует воспользоваться более точной формулой 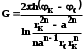 , (12) , (12)Эта формула при n=1 переходит в формулу определения дебита эксцентрично заложенной одиночной скважины (а - эксцентриситет скважины). В большинстве практических случаев можно пользоваться формулой (10), т.к. уже при rк=10а, дебиты подсчитанные по формулам (9) и (12), различаются не более чем на одну тысячную процента. Определим дебит батареи умножив формулу (10) на число скважин в батареи n 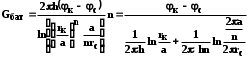 , (13) , (13)Рассмотрим поле течения в области действия круговой батареи, т.е. построим семейства линий тока и изобар. Уравнение изобар получаем из (6) путём представления радиусов rj в полярной системе координат. 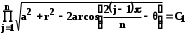 , (14) , (14)Данное уравнение позволяет построить поле изобар, а линии тока пересекают изобары под прямым углом. Плоскость течения (рис. 2) кольцевой батареи с n равнодебитными скважинами, размещенными в вершинах правильного многоугольника, делится на n равных частей (секторов) прямыми линиями тока Н, сходящимися в центре батареи и делящими расстояние между двумя соседними скважинами пополам. Эти линии тока называются нейтральными. Другое семейство прямых линий тока Г проходит через центры скважин и делит сектор, ограниченный двумя нейтральными линиями, пополам. Это - главные линии. Семейство изобар подразделяется на два подсемейства, которые разграничиваются изобарой пересекающей себя в центре батареи столько раз сколько скважин составляет данную батарею. Первое подсемейство изобар определяет приток к отдельным скважинам и представляет собой замкнутые, каплеобразные кривые, описанные вокруг каждой скважины. Второе семейство - определяет приток к батареи в целом и представляет собой замкнутые кривые, описанные вокруг батареи. 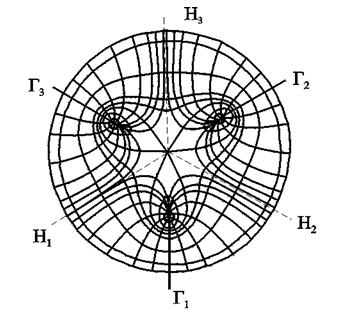 Рисунок 2 - Плоскость течения кольцевой батареи Скорость фильтрации по главным линиям максимальна, а по нейтральным линиям - минимальна. В центре кольцевой батареи скорость фильтрации равна нулю, т.е. частица жидкости, находящаяся в точке, в которой изобара пересекает сама себя, неподвижна. Такие точки фильтрационного поля называются точками равновесия и при разработке в окрестностях таких точек образуются “застойные области”. В условиях водонапорного режима в этих областях могут возникать “целики нефти”. Зная положения точек равновесия в пласте, можно находить рациональные приёмы для своевременной ликвидации целиков нефти. Одним из таких приёмов является изменение режима работы скважин, заставляющее нефть целика прийти в движение в нужном направлении. Для кольцевой батареи, на основе анализа формул (7) - (10), можно сделать ряд оценок эффекта взаимодействия: - дебит изменяется непропорционально числу скважин и радиусу батареи (расстоянию между скважинами); - с увеличением числа скважин дебит каждой скважины уменьшается при постоянном забойном давлении, т.е. растет эффект взаимодействия; - взаимодействие скважин может практически не проявляться только при очень больших расстояниях между скважинами (в случае несжимаемой жидкости, строго говоря, влияние скважин распространяется на весь пласт); - с увеличением числа скважин темп роста суммарного дебита батареи замедляется, а именно, сверх определённого предела увеличение числа скважин оказывается неэффективным в виду прекращения прироста дебита виду прекращения прироста дебита. Приток к прямолинейной батареи скважин Рассмотрим, как и в предыдущем случае, приток к батареи при удалённом контуре питания в режиме поддержания постоянного забойного давления. В отличии от круговой батареи необходимо различать два случая: - число скважин батареи нечетное; - число скважин четное. В обоих случаях дебиты скважин, равноудаленные от середины или от концов батареи, будут одинаковы, а при разной удаленности будут отличаться. Последнее вызывается не одинаковой интенсивностью влияния со стороны скважин батареи на те, или иные скважины. При этом при нечетном числе скважин дебит средней скважины отличается от дебитов других скважин. Дебиты равномерно расположенных скважин можно определить общим методом с использованием формулы (6). Можно вывести аналогичные уравнения для любой скважины прямолинейной батареи конечной длины в пласте с прямолинейным контуром питания, но с использованием дополнительно метода отображения. В этом случае запись уравнений оказывается громоздкой из-за необходимости учета не только взаимных расстояний между скважинами, но также расстояний между скважинами и воображаемыми источниками и расстояний между этими последними. Для практических расчетов можно использовать приближенную формулу П.П. Голосова для общего дебита скважин прямолинейной батареи: - для нечетного числа скважин 2n+1, где n - любое целое число. 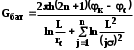 (15) (15)для четного числа скважин 2n 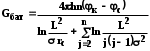  , (16) , (16)где h - толщина пласта; - расстояние между скважинами; L – расстояние до контура. Ошибка в определении дебитов по данным формулам не превышает 3-4% при L=10км, rс=10см при расстояниях между скважинами 100м 500м. Приведенные формулы можно использовать при любом контуре питания, т.к. проведенные ранее исследования взаимодействия двух скважин показали, что форма контура питания пласта мало влияет на взаимодействие скважин. Что касается расстояния скважин до контура питания, то по мере приближения скважин к контуру питания эффект взаимодействия уменьшается, но в реальных условиях значительного удаления скважин от контура питания погрешность определения расстояния до контура даже в 100% не отражается значительно на эффекте взаимодействия. Для однородных пластов и жидкостей относительные изменения дебитов скважин, вызванные эффектом взаимодействия, не зависят от физико-геологических характеристик пласта и от физических параметров жидкости. Рассмотрим теперь фильтрационное поле (рис. 3), поддерживаемое, для простоты, бесконечной цепочкой равностоящих скважин (требование бесконечности приводит к ликвидации граничных эффектов на концах батареи и равнодебитности скважин, т.к. все скважины оказываются в равных условиях притока к ним флюидов) [3]. 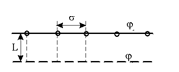 Рисунок 3 - Фильтрационное поле Для получения формул дебита скважины бесконечной прямолинейной батареи использует формулу (16) дебита скважины кольцевой батареи. Положим, что rк=l+a; a=n /(2 ), (17) где L=const - разность между радиусом контура питания и радиусом кольцевой батареи а; =const - длина дуги окружности радиусом а между двумя соседними скважинами кольцевой батареи. Подставив значения rк, a в формулу (16), получим 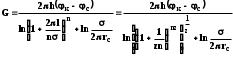 , (18) , (18)где z= / (2l). Переходя в данной формуле к пределу при n и учитывая, что 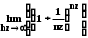 =e, получим формулу массового дебита скважины прямолинейной батареи =e, получим формулу массового дебита скважины прямолинейной батареи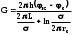 , (19) , (19)где L - расстояние от контура питания до батареи; - расстояние между скважинами батареи; h - толщина пласта. Суммарный дебит из n - скважин определится следующим выражением  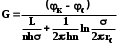 , (20) , (20)Для несжимаемой жидкости соотношение (20) можно переписать через давление и объёмный дебит  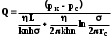 , (21) , (21)Ортогональная сетка, изображающая фильтрационное поле бесконечной прямолинейной батареи (рис. 4). Здесь, как и в кольцевой батарее, имеются главные и нейтральные линии тока, перпендикулярные цепочке. Нейтральными линиями тока вся плоскость течения делится на бесконечное число полос, каждая из которых является полосой влияния одной из скважин, находящейся в середине расстояния между двумя соседними нейтральными линиями. Главные линии тока проходят через центры скважин, параллельно нейтральным линиям. 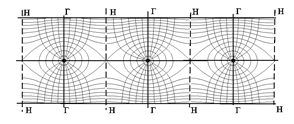 Рисунок 4 - Ортогональная сетка Изобара, бесчисленное множество раз пересекающая сама себя, отделяет изобары внешнего течения ко всей батареи, охватывающих всю цепочку скважин, от изобар притока к скважине, охватывающих только данную скважину. Точки пересечения граничной изобары являются точками равновесия и они делят интервал между двумя соседними скважинами пополам. 3. Анализ полученных результатов и выводы Заданный процесс является примером работы скважины на водонапорном режиме. Нефть вытесняется в добывающую скважину из продуктивного пласта под действием напора воды закачиваемого в нагнетательную скважину. В нефтеносном контуре образуются водная и нефтяная части, а так же водонефтяной контакт. При отборе жидкости из скважины частицы жидкости в пласте будут двигаться по горизонтальным прямолинейным траекториям, радиально сходящимся к центру скважины. Такой фильтрационный поток называется плоскорадиальным. В начальный момент времени, при наличии в пласте только нефти можно применить расчётную схему (рис.5) и зависимости для плоскорадиального фильтрационного потока.   Рисунок 5 – Схема плоскорадиального фильтрационного потока Результаты исследования скважины на нескольких режимах приведены в таблице 1. Таблица 1 – Результаты исследования скважины
Для того чтобы определить, по какому закону происходит фильтрация нефти в начальный момент времени, необходимо по данным исследования скважины построить индикаторную диаграмму (рис. 6). 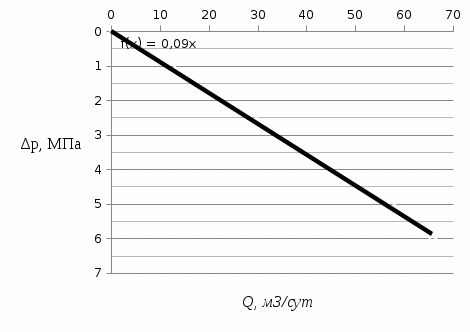 Рисунок 6 – Индикаторная диаграмма При этом наносятся точки, и подбирается теоретическая индикаторная диаграмма. В курсовой работе исследовалась взаимодействие скважин кольцевой батареи. В результате проведенных исследований было получено значение радиуса зоны проявления неньютоновских свойств нефти прямо пропорционально произведению коэффициента проницаемости на дебит скважины и обратно пропорционально мощности пласта и вязкости нефти с разрушенной структурой. В результате расчётов можно сделать вывод о том, что пласт обладает малой проницаемостью и для вытеснения всей нефти потребуется длительное время. При разработке месторождения выгоднее добывать нефть при естественном режиме работы пласта. Система поддержания пластового давления с помощью закачки воды является эффективным способом повышения нефтеотдачи пласта. СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ 1. Басниев и др. Подземная гидравлика: Учебник для вузов.-М.: Недра, 1986 г. 2.Чарный, Подземная гидрогазодинамика, 1963 г. 3.Щелкачев, Разработка нефтеводоносных пластов при упругом режиме, 1959 г. 4.Пермяков, Методика анализа разработки нефтяных месторождений, 1962 г. 5.Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидромеханика: Учебник для ВУЗов. - М.: Недра, 1993. 6.Евдокимова В.А. Сборник задач по подземной гидравлике / Евдокимова В.А., Кочина И.Н.: Учебное пособие для вузов. – 2-е изд., стереотипное. Перепечатка с издания 1979 г. – М.: ООО ИД «Альянс», 2007. – 168 с. 7.Телков А.П. Прикладные задачи разработки нефтегазоконденсатных месторождений и нефтегазодобычи. - М.: ЦентрЛитнефтеГаз, 2008. - 512 с. Фанчи Д.Р. Интегрированный подход к моделированию фильтрационных потоков. 2010 г. - 256 с. |
