Курсовавя ТММ2. Исследовать и спроектировать механизм качающегося контейнера
 Скачать 119.83 Kb. Скачать 119.83 Kb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ОРЕНБУРГСКИЙ ГОСУДАРСТВЕННЫЙ АГРАРНЫЙ УНИВЕРСИТЕТ» Факультет/институт: Инженерный Кафедра «Технический сервис» Расчетно-пояснительная записка к курсовому проекту По дисциплине: «Теория машин и механизмов» На тему: «Исследовать и спроектировать механизм качающегося контейнера» Задание 2, вариант 2 Выполнил студент: Баканов С.А. Группа: тех. сервис-21 Проверил преподаватель: кандидат технических наук, доцент Петров А.А.  Оренбург 2021 г. Содержание Кинематическое исследование шарнирно-рычажного механизма качающегося конвейера…………………………………………………………………………… 4 Структурный анализ механизма………………………………………………. 4 1.1.1 Степень подвижности всего механизма………………………………... 4 1.1.2 Определение групп Ассура……………………………………………... 5 1.1.3 Определение класса, порядка и вида каждой группы……………........ 6 1.1.4 Определение класса всего механизма………………………………….. 6 Кинематические параметры механизма………………………………………. 6 Планы положений звеньев механизма………………………………………... 7 Планы скоростей и ускорений………………………………………………… 7 Кинематические диаграммы…………………………………………………. 11 Выводы по первому листу……………………………………………………. 12 Проектирование кулачкового механизма……………………………………….. 14 Кинематические параметры толкателя……………………………………… 14 Определение минимального радиуса кулачка с поступательным движением толкателя и башмаком в виде плоской тарелки…………………………….. 14 Профилирование кулачка, башмак которого плоская тарелка……………. 14 Выбор диаметра тарелки……………………………………………………... 14 Выводы по второму листу……………………………………………………. 15 Построение диаграмм энергетических параметров механизма…………… 23 Определение момента инерции маховика…………………………………... 23 Выводы по четвертому листу………………………………………………... 24 3. Список литературы………………………………………………………………... 26  1. Кинематическое исследование шарнирно-рычажного механизма качающегося конвейера 1. Кинематическое исследование шарнирно-рычажного механизма качающегося конвейераИз разработанных методов кинематического исследования механизмов в настоящее время все чаще используется аналитический метод. Аналитический метод кинематического исследования заключается в том, что выводятся аналитические уравнения, связывающие известные параметры входного (ведущего) звена с неизвестными параметрами ведомых звеньев. Используя эти уравнения, можно посчитать, с наперед заданной точностью, интересующие нас кинематические параметры (перемещения, скорости и ускорения, как линейные, так и угловые) ведомых звеньев и в первую очередь выходного звена (звена, на котором находится рабочий орган механизма). 1.1 Структурный анализ механизма Механизм привода качающегося конвейера представленного на рис.1 состоит из следующих звеньев: АВ=0,31 м -длинна стойки ,О1О3 =0,27 м – расстояние между стойками, стойка (ведущее звено) АО1=0,1 м, ВO3 =0,2 м –длинна стойки, 5(С) – кулисный камень, ВС=1 м. Рис. 1. Схема шарнирно-рычажного механизма качающегося конвейера. 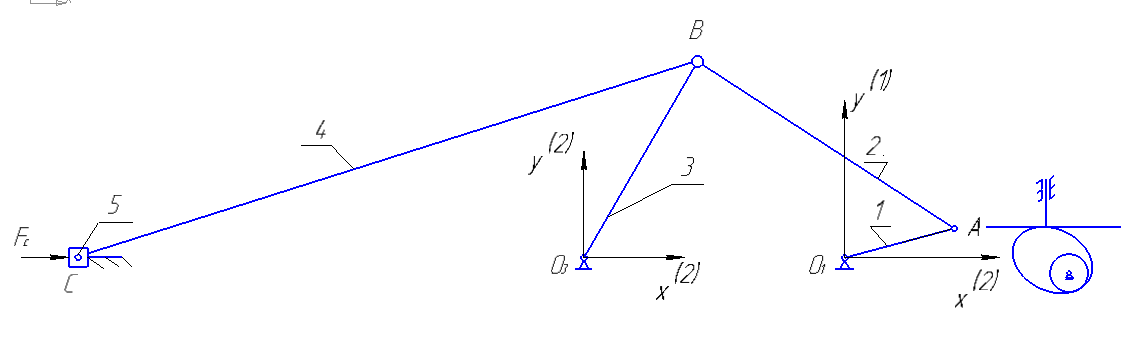 Кинематические пары: 1 Стойка О1 – кривошип О1А: 5 класса, вращательное движение. 2 Кривошип О1А – звено АВ: 5 класса, плоскопараллельное движение. 3 Стойка О3 – кривошип О3В: 5 класса, вращательное движение. 4 Кривошип О3В- звено АВ: 5 класса, плоскопараллельное движение. 5 Кривошип О3В- звено ВС: 5 класса, плоскопараллельное движение. 6 Кулисный камень С –звено ВС: 5 класса, поступательное. 7 Выходное звено 5 – направляющие: 5 класса, поступательное. 1.1.1 Степень подвижности всего механизма Данный механизм является плоским, так как все его звенья движутся в параллельных плоскостях, и оси вращательных кинематических пар параллельны. Следовательно, степень подвижности всего механизма определяется по формуле Чебышева: 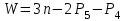 , (1.1) , (1.1)где n – подвижное число звеньев; Р5 – число кинематических пар пятого класса; Р4 – число кинематических пар четвертого класса. В исследуемом механизме число подвижных звеньев – 5, число кинематических пар пятого класса - 7, число кинематических пар четвертого класса – 0. 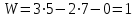 . .Данная кинематическая цепь является механизмом, так как степень подвижности равна 1, что соответствует числу заданных законов движения. 1.1.2 Определение групп Ассура Отсоединяем наиболее удаленные от ведущего звена части механизма с наименьшим четным числом звеньев. Такими являются звенья 4 и 5. Проверяем степень подвижности отсоединенной и оставшейся частей. Первая отсоединенная группа. 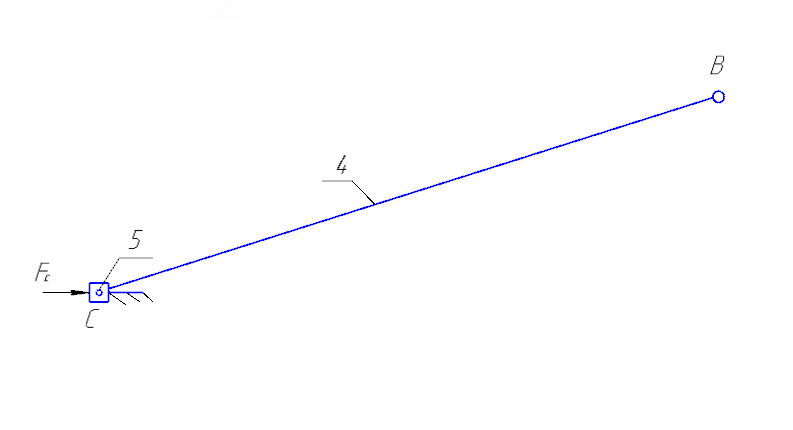 2 класс 2 порядок 2 вид 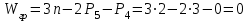 ; ;Следовательно, отсоединенная группа является группой Ассура. 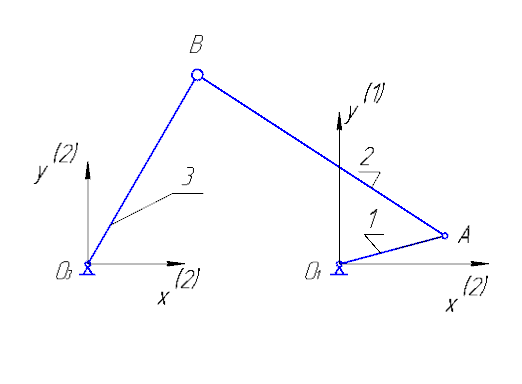 Оставшаяся часть.  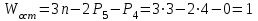 , значит оставшаяся часть является механизмом. , значит оставшаяся часть является механизмом.От оставшейся части отсоединяем еще одну наиболее удаленную от ведущего звена кинематическую цепь и проверяем те же условия. Вторая отсоединенная группа. 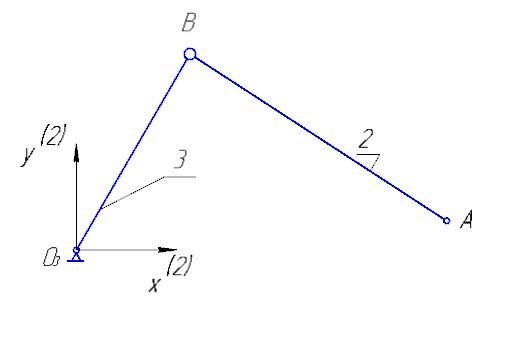 2 класс 2 порядок 1 вид 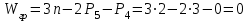 , следовательно, отсоединенная группа является группой Ассура. , следовательно, отсоединенная группа является группой Ассура.Оставшаяся часть. 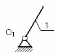 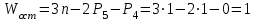 , значит, оставшаяся часть является механизмом. , значит, оставшаяся часть является механизмом.1.1.3 Определение класса, порядка и вида каждой группы Разложение начинаем с выходного (пятого) звена. Первая отсоединенная группа Ассура (4-5) – второго класса, второго порядка, второго вида. Вторая группа состоит из второго и третьего звеньев - второго класса, второго порядка, первого вида. Входное звено и стойка образуют механизм 1 класса. 1.1.4 Определение класса всего механизма Класс всего механизма определяем по наивысшему классу группы, входящий в механизм, следовательно, класс всего механизма – второй. Вывод: механизм качающегося конвейера станка является механизмом 2 класса, состоящий из механизма 1 класса и двух присоединенных групп: I группа – 2 класса, 2 порядка, 2 вида; II группа – 2 класса, 2 порядка, 1 вида. 1.2 Кинематические параметры механизма В задачу кинематического анализа входит определение законов движения звеньев механизма вне зависимости от сил, действующих на эти звенья определение скоростей и ускорений точек и угловых скоростей и ускорений звеньев. 1.3 Планы положений звеньев механизма Планы положений строим для 12-ти положений механизма. Длины звеньев откладываем в определенном графическом масштабе по ГОСТу. Положения определяются поворотом ведущего звена через каждые 300 от оси X(I) в сторону оси Y(I), начиная с первого положения соответствующего 150. Планы положений строятся графическим методом. Положения I =300 и II =1200 изображаем сплошной и пунктирной линиями соответственно. Индексы положений у букв, обозначающих кинематические пары, проставляем сверху. На планах положений изображаем системы координат для каждого контура. 1.4 Планы скоростей и ускорений Построение планов скоростей и ускорений основано на графическом решении векторных уравнений. Планы скоростей и ускорений строим для двух расчетных положений механизма в соответствующем масштабе. Масштабный коэффициент для каждого плана скоростей и ускорений может быть свой. Из полюса Р плана скоростей откладываем векторы скоростей всех точек механизма, вычисленные для этого положения. При этом учитывается направление углов в системах координат контура. Из полюса откладываем ускорения точек. Их направления при вращательном движении определяются тангенциальными и нормальными ускорениями. Определение линейных скоростей и ускорений точек механизма начинается с механизма первого класса, а затем производится в порядке присоединения групп Ассура. Рассмотрим построение планов скоростей для заданных положений механизма. Модуль скорости точки А кривошипа, совершающего вращательное движение относительно стойки, определим: VА= ω1 ∙ ℓО1А м/с, (1.2) VА= 12 ∙ 0,1 = 1,2 м/с Вектор скорости VА направлен перпендикулярно радиусу кривошипа в сторону его вращения. Выбираем масштабный коэффициент μν таким образом чтобы отрезок, изображающий скорость точки А, был не меньше 120 мм. Если μ ν=0,06 (м•с‾¹)/мм, тогда ра= VА/ μ l=1,2/0,01=120 мм. Из произвольной точки р – полюса плана скоростей откладываем в указанном направлении отрезок ра. Для определения скоростей точек в структурной группе составляют два векторных уравнения, связывающих искомую скорость точки с известными скоростями точек. В группе Ассура (2,3) определяем скорость центра шарнира В, который соединяет звенья 2 и 3. Рассматривая движение точки В по отношению к точке А, а затем по отношению к точке С, запишем 2 векторных уравнения (по одному для каждого звена группы Ассура): Система векторных уравнений: 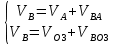 (1.3) (1.3)VBA перпендикулярен AB VО3=0; VBО3 перпендикулярен BО3 В этой системе векторных уравнений известны по модулю и направлению векторы скоростей точек А и О3. VО3 = 0, так как в точке О3 звено ВО3 образует вращательную кинематическую пару со стойкой. Векторы относительных скоростей известны по линии действия. Скорость VВА направлена перпендикулярно к звену АВ, а скорость VВО3 направлена перпендикулярно к звену ВО3. Решаем векторные уравнения графически. Согласно первому уравнению, через точку а проводим прямую перпендикулярно звену АВ, а согласно второму, через точку р (так как VО3 = 0 и точка с лежит в полюсе) проводим прямую перпендикулярно к ВО3. На пересечении этих перпендикуляров отмечаем точку b , которая является концом вектора рb, изображающего абсолютную скорость точки В. Направление скорости VВА определяем в соответствии с уравнением (VB=VА+VBA ). В группе Ассура (4,5) определяем скорость точки C, которая одно- временно принадлежит звену 4 и звену 5. Запишем векторные уравнения : 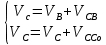 (1.4) (1.4)VCB перпендикулярен CB VC горизонтален В соответствии с векторным уравнением через конец вектора VВ (точку b) проводим линию действия вектора VСВ , а через полюс p – направление вектора VС . Точку пересечения этих направлений обозначим буквой d. Находим скорости: VА= ω1 ∙ ℓО1А = 12 ∙ 0,1 = 1,2 м/с, Для φ=30о VВ=рb∙ μV=112,14∙ 0,01 =1,1214 м/с, VС = рc ∙ μV=101,65∙ 0,01 =1,0165 м/с, VВА=аb ∙ μV=58,41∙ 0,01=0,5841 м/с, VCВ=bc ∙ μV=31,7∙ 0,01=0,317 м/с. Для φ=120о VВ = рb ∙ μV=74,46 ∙ 0,01=0,7446 м/с, VС = рc ∙ μV=72,35 ∙ 0,01=0,7235 м/с, VВА= аb ∙ μV =54,065 ∙ 0,01=0,541 м/с, VCВ= bc ∙ μV =34,67 ∙0,01=0,3467 м/с. Находим угловые скорости ω2, ω3 и ω4 звеньев 2 , 3 и 4. ω=V/ℓ c-1; (1.5) Для φ=30о ω 1=12 с‾¹, ω 2=VВА/ℓАВ=0,5841/0,31=1,88 с‾¹, ω3=VВО3/ℓВО3=VВ/ℓВО3=1,1214/0,2=5,6 с‾¹, ω4=VСВ/ℓСВ= 0,317 /1 = 0,317 с‾¹. Для φ=120о ω 1=12 с‾¹, ω 2 =VВА/ℓАВ = 0,541/0,31= 1,75 с‾¹, ω3=VВО3/ℓВО3=VВ/ℓВО3=0,7446/0,2=3,72 с‾¹, ω4=VСВ/ℓСВ= 0,3467/1 = 0,3467 с‾¹. Рассмотрим построение планов ускорений для заданных положений механизма. Для механизма первого класса в первом приближении определяем ускорение аА точки А, совершающей вращательное движение по окружности радиуса ℓО1А с постоянной угловой скоростью (ω1=const), т.е. принимаем, что ε1=0. аА = аnА = ω1² ∙ ℓО1А; (1.6) Для φ=30о аА=122*0,1=14,4 м/с², Для φ=120о аА=122*0,1=14,4 м/с². Вектор ускорения аА=аnА направлен по звену О1А от точки А к точке О1. Задаемся значением масштабного коэффициента плана ускорений μа= 0,1 м∙c‾²/мм , тогда отрезок πа, изображающий ускорение аА , определится : πа= аА/μ ν =0,5/0,1=144 мм. Отложив из произвольно взятой точки π (полюса плана ускорений) вектор πапараллельно О1А, получим план ускорений для механизма первого класса. В группе Ассура (2,3) определяем ускорение точки В. Рассматривая движение точки В сначала по отношению к точке А (относительное движение звена 2 – вращательное вокруг точки А), а затем по отношению к точке О3 (относительное движение звена 3 – вращательное вокруг точки О3), запишем соответственно два векторных уравнения: 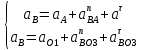 (1.7) (1.7)Ускорения аА и аO1 точек А и O1 известны (аO1 = 0). Величины нор- мальных ускорений вычисляются по формулам : аnВА = ω2²∙ℓАВ м/с², (1.8) аnВO3 =ω3²∙ℓВO3 м/с². (1.9) Для φ=30о Для φ=120о аnВА=1,882*0,31=1,096 м/с², аnВА=1,752*0,31=0,949 м/с², аnВO3=5,62*0,2=6,272 м/с². аnВO3=3,722*0,2=2,768 м/с². Вектор аnВА направлен параллельно звену АВ от точки В к точке А ; Вектор аnВО3 параллелен звену ВО3 и направлен от точки В к точке О3 . У векторов тангенциальных ускорений aτВА и аτВС известны только  ВА линии действия :aτ ⊥ АВ, аτВО3 ⊥ ВО3. Вектор полного ускорения аВ и величины тангенциальных ускорений aτВА и aτВD определяются построением плана ускорений. Для графического решения системы векторных уравнений определим величины отрезков, изображающих нормальные ускорения аnВА и аnВС : аn2 = аnВА / μамм, (1.10) аn3 = аnВО3 / μамм. (1.11) Для φ=30о. Для φ=120о аn2=1,096/0,1=10,96 мм, аn2=0,949/0,1=9,49 мм, аn3=6,272/0,1=62,72 мм. аn3=2,768/0,1=27,68 мм. Теперь можно решать векторные уравнения. В соответствии с первым векторным уравнением из точки а следует отложить отрезок аn2, который будет изображать аnВА. Отрезок аn2 проводим параллельно звену АВ в направление от точки В к точке А. Через точку n2 проводим перпендикуляр к звену АВ в направление вектора aτВА. В соответствии со вторым векторным уравнением из точки π (так как аО3 = 0) параллельно звену ВО3 в направлении от В к О3 отложим отрезок πn3, изображающий ускорение аnВО3. Через точку n3 перпендикулярно звену ВО3 проводим направление вектора aτВО3 до пересечения в точке b с направлением ускорения aτВА. Соединим полученную точку bс полюсом π, получим отрезок πb, который изображает ускорение аВ, а отрезки n2b и n3b - соответственно тангенциальные ускорения aτВА и aτВО3. Направление векторов расставляем в соответствии с векторными уравнениями. Соединив точки а и b, получим от- резок аb, изображающий вектор aВА полного ускорения точки В относительно точки А. План ускорений для группы (2,3) построен. Для группы (4,5) запишем векторное уравнение: 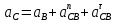 (1.12) (1.12)В этом уравнении вектор аВ известен по величине и направлению. Величину нормального ускорения аnCВ точки C относительно точки В определим: 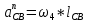 (1.13) (1.13)Для φ=30о. Для φ=120о 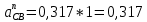 м/с² м/с² 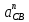 =0,3467 *1=0,3467 м/с² =0,3467 *1=0,3467 м/с²Вектор ускорения 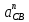 направлен параллельно звену СВ от точки С к точке В. направлен параллельно звену СВ от точки С к точке В.Направление вектора тангенциального ускорения 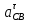 точки С относительно точки В известно: точки С относительно точки В известно: 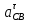 перпендикулярно СВ и перпендикулярно СВ и 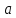 с параллелен направлению движения ползуна. с параллелен направлению движения ползуна.Решаем уравнение графически. В соответствии с уравнением из точки b плана ускорений откладываем отрезок bn4, изображающий ускорение аnСВ : bn4 = аnСВ /μа, мм. (1.14) Для φ=30о. Для φ=120о bn4=0,317/0,1=3,17 мм. bn4=0,3467/0,1=3,467 мм. Отрезок bn4 проводим параллельно звену СВ в направлении от точки С к точке В. Через точку n4 проводим перпендикулярно СВ направление аnСВ. Из точки π проводим параллельно направлению движения ползуна направление вектора аС. Эти направления пересекутся в точке с . Соединив на плане точки b и с, получим вектор bс, изображающий ускорение аСВ (полное ускорение точки С относительно точки В). План ускорений построен, из плана определим величины ускорений: аВ = (πb) ∙ μа м/с², (1.15) аC = (πd) ∙ μа м/с². (1.16) Для φ=30о. Для φ=120о аВ=80,72*0,1=8,072 м/с², аВ=179,41*0,1=17,941 м/с², аC=72,02*0,1=7,202 м/с². аC=183,99*0,1=18,399 м/с². 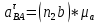 м/с², (1.17) м/с², (1.17)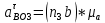 м/с², (1.18) м/с², (1.18)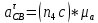 м/с². (1.19) м/с². (1.19)Для φ=30о. Для φ=120о 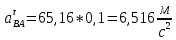 , , 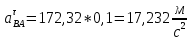 , ,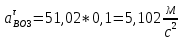 , , 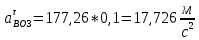 , ,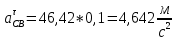 . . 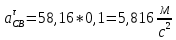 . .Величины угловых ускорений ε2 , ε3 и ε4 звеньев 2, 3, 4 определим следующим образом: 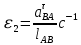 , (1.20) , (1.20)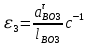 , (1.21) , (1.21)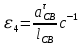 . (1.22) . (1.22)Для φ=30о. Для φ=120о 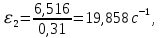 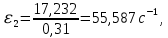 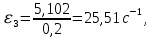 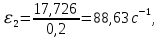 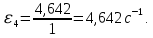 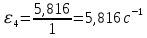 . .1.5 Кинематические диаграммы Диаграммы перемещения (S), скорости (V) и ускорения (W) строим для выходного звена качающегося конвеинера. Диаграммы строим для полного оборота ведущего звена с 12-го по 12-ое положение. Проводим оси систем координат, выбираем масштабный коэффициент и изображаем масштабную сетку. Ось ординат проводим между 12-м и 1-м положением механизма. По оси абсцисс откладываем положения ведущего звена в зависимости от угла поворота. По оси ординат откладываем перемещение, скорость и ускорение точки В на соответствующих графиках. Данные для построения диаграмм берем из распечаток, сделанных при помощи ЭВМ. Полученные расчеты приводятся в нижеследующей таблицах 1.1. и 1.2. 1.6 Выводы по первому листу: Механизм спроектированного качающегося конвейера является работоспособным. Это доказывается следующим: Диаграммы скорости и перемещения – плавные кривые линии без разрывов и скачков. Анализируя диаграммы, мы видим, что точки перегибания функций соответствуют max и min производной от этой функции, а производная от max и min функции равны нулю. Это значит, что все расчеты выполнены правильно. Для всех двенадцати положений механизма его заклинивание не произойдет, потому что как видно из кинематической схемы, представленной на первом листе, механизм делает полный оборот, и заклинивания при этом не происходит. Планы скоростей и ускорений построены правильно. Таблица 1.1 КУРСОВОЙ ПРОЕКТ по ТММ. ПЕРВЫЙ ЛИСТ 1 -ая пpисоединенная гpуппа 1 -го вида. Длина ведущего звена, м . . . . . . . . . . . . . . . . L1 = 0.100 Отношение длин звеньев. . . . . . . . . . . . . . . .LAM01 = 2.700 Отношение длин звеньев. . . . . . . . . . . . . . . .LAM21 = 3.100 Отношение длин звеньев. . . . . . . . . . . . . . . .LAM31 = 2.000 ╔══════════════════════════════════════════════════════════╤═══════════╗ ║ Наименование паpаметpа │обозначение║ ╠══════════════════════════════════════════════════════════╪═══════════╣ ║ Угол повоpота ведущего звена , гpд . . . . . . . . . .│ F1 ║ ║ Угол повоpота шатуна , гpд . . . . . . . . . .│ F2 ║ ║ Угол повоpота коpомысла , гpд . . . . . . . . . .│ F3 ║ ║ Угловая скоpость ведущего звена, pад/с . . . . . . . . .│ W1 ║ ║ Угловая скоpость шатуна , pад/с . . . . . . . . .│ W2 ║ ║ Угловая скоpость коpомысла , pад/с . . . . . . . . .│ W3 ║ ║ Линейная скоpость точки Aо , м/с . . . . . . . . . .│ VAo ║ ║ Линейная скоpость точки Bо , м/с . . . . . . . . . .│ VBo ║ ║ Угловое ускоpение ведущего звена, pад/(с*с) . . . . . . .│ E1 ║ ║ Угловое ускоpение шатуна , pад/(с*с) . . . . . . .│ E2 ║ ║ Угловое ускоpение коpомысла , pад/(с*с) . . . . . . .│ E3 ║ ║ Тангенциальное ускоpение точки A, м/(с*с) . . . . . . . .│ WAt ║ ║ Ноpмальное ускоpение точки A, м/(с*с) . . . . . . . .│ WAn ║ ║ Полное ускоpение точки A, м/(с*с) . . . . . . . .│ WAo ║ ║ Тангенциальное ускоpение точки B, м/(с*с) . . . . . . . .│ WBt ║ ║ Ноpмальное ускоpение точки B, м/(с*с) . . . . . . . .│ WBn ║ ║ Полное ускоpение точки B, м/(с*с) . . . . . . . .│ WBo ║ ╚══════════════════════════════════════════════════════════╧═══════════╝ ╔════╤══════════╤══════════╤══════════╤══════════╤══════════╤══════════╗ ║ N │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 ║ ╠════╪══════════╪══════════╪══════════╪══════════╪══════════╪══════════╣ ║ F1 │ 15.000│ 45.000│ 75.000│ 105.000│ 135.000│ 165.000║ ║ F2 │ -29.000│ -23.000│ -19.000│ -18.000│ -20.000│ -28.000║ ║ F3 │ 62.000│ 74.000│ 89.000│ 105.000│ 117.000│ 120.000║ ║ W1 │ 12.000│ 12.000│ 12.000│ 12.000│ 12.000│ 12.000║ ║ W2 │ 2.810│ 1.884│ 0.984│ -0.034│ -1.744│ -5.219║ ║ W3 │ 4.163│ 5.607│ 6.305│ 5.971│ 3.723│ -2.654║ ║ VAo│ 1.200│ 1.200│ 1.200│ 1.200│ 1.200│ 1.200║ ║ VBo│ 0.833│ 1.121│ 1.261│ 1.194│ 0.745│ -0.531║ ║ E1 │ 0.000│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000║ ║ E2 │ -20.833│ -20.972│ -20.803│ -27.897│ -55.546│ -97.224║ ║ E3 │ 39.758│ 25.390│ 5.746│ -23.963│ -88.563│ -201.496║ ║ WAt│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000║ ║ WAn│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400║ ║ WAo│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400║ ║ WBt│ 7.952│ 5.078│ 1.149│ -4.793│ -17.713│ -40.299║ ║ WBn│ 3.466│ 6.287│ 7.952│ 7.131│ 2.772│ 1.409║ ║ WBo│ 8.674│ 8.082│ 8.034│ 8.592│ 17.928│ 40.324║ ╚════╧══════════╧══════════╧══════════╧══════════╧══════════╧══════════╝ ╔════╤══════════╤══════════╤══════════╤══════════╤══════════╤══════════╗ ║ N │ 7 │ 8 │ 9 │ 10 │ 11 │ 12 ║ ╠════╪══════════╪══════════╪══════════╪══════════╪══════════╪══════════╣ ║ F1 │ 195.000│ 225.000│ 255.000│ 285.000│ 315.000│ 345.000║ ║ F2 │ -45.000│ -59.000│ -61.000│ -56.000│ -47.000│ -37.000║ ║ F3 │ 103.000│ 78.000│ 61.000│ 53.000│ 50.000│ 53.000║ ║ W1 │ 12.000│ 12.000│ 12.000│ 12.000│ 12.000│ 12.000║ ║ W2 │ -7.335│ -3.136│ 1.083│ 3.224│ 3.882│ 3.601║ ║ W3 │ -9.900│ -8.603│ -4.922│ -2.097│ 0.159│ 2.248║ ║ VAo│ 1.200│ 1.200│ 1.200│ 1.200│ 1.200│ 1.200║ ║ VBo│ -1.980│ -1.721│ -0.984│ -0.419│ 0.032│ 0.450║ ║ E1 │ 0.000│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000║ ║ E2 │ 36.742│ 117.420│ 71.555│ 29.537│ 2.617│ -13.893║ ║ E3 │ -67.530│ 84.403│ 75.489│ 56.086│ 48.979│ 46.698║ ║ WAt│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000│ 0.000║ ║ WAn│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400║ ║ WAo│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400│ 14.400║ ║ WBt│ -13.506│ 16.881│ 15.098│ 11.217│ 9.796│ 9.340║ ║ WBn│ 19.603│ 14.801│ 4.846│ 0.879│ 0.005│ 1.011║ ║ WBo│ 23.805│ 22.450│ 15.856│ 11.252│ 9.796│ 9.394║ ╚════╧══════════╧══════════╧══════════╧══════════╧══════════╧══════════╝ Таблица 1.2 КУРСОВОЙ ПРОЕКТ по ТММ. ПЕРВЫЙ ЛИСТ 2 -ая пpисоединенная гpуппа 2 -го вида. Длина ведущего звена, м . . . . . . . . . . . . . . . . L1 = 0.200 Отношение длин звеньев. . . . . . . . . . . . . . . .LAM01 = 0.000 Отношение длин звеньев. . . . . . . . . . . . . . . .LAM21 = 5.000 Ведущее звено для этой гpуппы . . . . . . . . . . . . . . . 3 ╔══════════════════════════════════════════════════════════╤═══════════╗ ║ Наименование паpаметpа │обозначение║ ╠══════════════════════════════════════════════════════════╪═══════════╣ ║ Угол повоpота ведущего звена , гpд . . . . . . . . . .│ F1 ║ ║ Угол повоpота шатуна , гpд . . . . . . . . . .│ F2 ║ ║ Линейное пеpемещение ползуна , м . . . . . . . . . . .│ S ║ ║ Угловая скоpость ведущего звена, pад/с . . . . . . . . .│ W1 ║ ║ Угловая скоpость шатуна , pад/с . . . . . . . . .│ W2 ║ ║ Линейная скоpость точки Aо , м/с . . . . . . . . . .│ VAo ║ ║ Линейная скоpость точки B , м/с . . . . . . . . . .│ VB ║ ║ Угловое ускоpение ведущего звена, pад/(с*с) . . . . . . .│ E1 ║ ║ Угловое ускоpение шатуна , pад/(с*с) . . . . . . .│ E2 ║ ║ Тангенциальное ускоpение точки A, м/(с*с) . . . . . . . .│ WAt ║ ║ Ноpмальное ускоpение точки A, м/(с*с) . . . . . . . .│ WAn ║ ║ Полное ускоpение точки A, м/(с*с) . . . . . . . .│ WAo ║ ║ Линейное ускоpение точки B, м/(с*с) . . . . . . . .│ WB ║ ╚══════════════════════════════════════════════════════════╧═══════════╝ ╔════╤══════════╤══════════╤══════════╤══════════╤══════════╤══════════╗ ║ N │ 1 │ 2 │ 3 │ 4 │ 5 │ 6 ║ ╠════╪══════════╪══════════╪══════════╪══════════╪══════════╪══════════╣ ║ F1 │ 62.000│ 74.000│ 89.000│ 105.000│ 117.000│ 120.000║ ║ F2 │ 10.000│ 11.000│ 12.000│ 11.000│ 10.000│ 10.000║ ║ S │ -0.889│ -0.926│ -0.976│ -1.031│ -1.076│ -1.084║ ║ W1 │ 4.163│ 5.607│ 6.305│ 5.971│ 3.723│ -2.654║ ║ W2 │ 0.403│ 0.317│ 0.023│ -0.306│ -0.347│ 0.267║ ║ VВo│ 0.833│ 1.121│ 1.261│ 1.194│ 0.745│ -0.531║ ║ VС │ -0.661│ -1.016│ -1.256│ -1.215│ -0.723│ 0.508║ ║ E1 │ 39.758│ 25.390│ 5.746│ -23.963│ -88.563│ -201.496║ ║ E2 │ 0.781│ -4.700│ -8.093│ -5.787│ 5.765│ 19.037║ ║ WAt│ 7.952│ 5.078│ 1.149│ -4.793│ -17.713│ -40.299║ ║ WAn│ 3.466│ 6.287│ 7.952│ 7.131│ 2.772│ 1.409║ ║ WAo│ 8.674│ 8.082│ 8.034│ 8.592│ 17.928│ 40.324║ ║ WB │ -8.345│ -7.427│ -2.911│ 5.405│ 18.157│ 39.085║ ╚════╧══════════╧══════════╧══════════╧══════════╧══════════╧══════════╝ ╔════╤══════════╤══════════╤══════════╤══════════╤══════════╤══════════╗ ║ N │ 7 │ 8 │ 9 │ 10 │ 11 │ 12 ║ ╠════╪══════════╪══════════╪══════════╪══════════╪══════════╪══════════╣ ║ F1 │ 103.000│ 78.000│ 61.000│ 53.000│ 50.000│ 53.000║ ║ F2 │ 11.000│ 11.000│ 10.000│ 9.000│ 9.000│ 9.000║ ║ S │ -1.025│ -0.940│ -0.889│ -0.866│ -0.861│ -0.868║ ║ W1 │ -9.900│ -8.603│ -4.922│ -2.097│ 0.159│ 2.248║ ║ W2 │ 0.444│ -0.359│ -0.479│ -0.257│ 0.021│ 0.271║ ║ VВo│ -1.980│ -1.721│ -0.984│ -0.419│ 0.032│ 0.450║ ║ VС │ 2.018│ 1.614│ 0.780│ 0.293│ -0.021│ -0.318║ ║ E1 │ -67.530│ 84.403│ 75.489│ 56.086│ 48.979│ 46.698║ ║ E2 │ -16.428│ -11.228│ 3.061│ 6.171│ 6.310│ 4.821║ ║ WAt│ -13.506│ 16.881│ 15.098│ 11.217│ 9.796│ 9.340║ ║ WAn│ 19.603│ 14.801│ 4.846│ 0.879│ 0.005│ 1.011║ ║ WAo│ 23.805│ 22.450│ 15.856│ 11.252│ 9.796│ 9.394║ ║ WB │ 14.476│ -21.623│ -14.812│ -8.419│ -6.582│ -7.259║ ╚════╧══════════╧══════════╧══════════╧══════════╧══════════╧══════════╝ 2.Проектирование кулачкового механизма С помощью динамического синтеза кулачкового механизма по заданному закону ускорения толкателя в соответствии с заданным видом диаграммы, по углу поворота толкателя и фазовым углом определяем наименьший размер кулачка и строим его профиль. 2.1 Кинематические параметры толкателя Синтез кулачкового механизма начинается с построения диаграммы перемещения толкателя, исходя из заданной диаграммы ускорения типа «Г». По оси абсцисс системы координат откладываем фазовые углы: удаления, дальнего стояния и возвращения. Фазовые углы делим на восемь равных частей. 2.2 Определение минимального радиуса кулачка с поступательным движением толкателя и башмаком в виде плоской тарелки. Как правило в таких механизмах плоскость тарелки делается под углом 900 к оси толкателя и поэтому угол передачи движения в любом положении кулачка равен 900, т.е. первое условие выбора минимального радиуса кулачка выполняется. Для выполнения второго условия необходимо чтобы профиль кулачка всюду был выпуклым. Для этого достаточно, чтобы минимальный радиус кулачка удовлетворял условию: rmin > - ((S-S0)+ 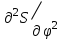 ), (2.1) ), (2.1)В этом случае строят диаграмму зависимости (S-S0)+ 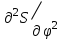 от от 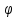 и определяют минимальный радиус большим или равным наибольшей по абсолютной величине отрицательной ординаты диаграммы. и определяют минимальный радиус большим или равным наибольшей по абсолютной величине отрицательной ординаты диаграммы.Получаем rmin=92 мм. 2.3 Профилирование кулачка, башмак которого плоская тарелка. Из произвольно выбранного центра О1 проводим окружность радиусом rmin. Затем откладываем углы удаления, дальнего стояния и возвращения. Углы удаления и возвращения делим на 8 равных частей и проводим лучи.На этих лучах откладываем значения (S-S0) от окружности радиусом rmin.В полученных точках строим тарелки перпендикулярно лучам. В полученной замкнутой области проводим кривую наиболее приближенную к тарелкам. Полученная кривая будет практическим профилем кулачка. 2.4 Выбор диаметра тарелки После определения минимального радиуса кулачка и построения профиля кулачка выбираем диаметр тарелки. RТ= 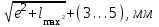 , (2.2) , (2.2)где е-дезаксиал толкателя, мм; 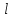 max- максимальное расстояние от оси толкателя до точки касания тарелкой профиля кулачка. max- максимальное расстояние от оси толкателя до точки касания тарелкой профиля кулачка.Окончательно принимаем dт=36 мм. 2.5 Выводы по второму листу: Кулачковый механизм спроектирован правильно, т.е. он работоспособен, так как нет заклинивания и получилось контактное касание тарелки и кулачка. Правильность расчетов подтверждается графиком ускорений, который соответствует типовому закону движения толкателя типа «Г» , а также графиками перемещения, скорости и ускорения, т.е. где у функции перемещения наблюдаются экстремумы скорость равна нулю, в точках, где график перемещения имеет перегибы график скорости имеет экстремумы. То же самое наблюдается у графиков скорости и ускорения. ТММ. Курсовой проект. Второй лист. Таблица 2.1 Исходные данные:
Таблица 2.2 Результаты вычисления:
Список литературы 1. Теория механизмов и машин / под ред. К.В. Фролова. – М.: Высш. шк., 1998. – 496 с. 2. Марголин, Ш.Ф. Теория механизмов и машин: теория, примеры и граф. работы / Ш.Ф. Марголин. – Минск: Вышейшая школа, 1968. – 359 с. 3. Теория механизмов и механика машин: учебник для вузов по машиностроит. направлениям и специальностям / под ред. Г.А. Тимофеева; [К.В. Фролов, С.А. Попов, А.К. Мусатов, Г.А. Тимофеев]. – 6-е изд., испр. и доп. – М.: МГТУ, 2009. – 686 с. 4. Артоболевский, И.И. Теория механизмов и машин: учебник для втузов / И.И. Артоболевский. – Изд. 6-е, стер., перепеч. с 4-го изд. 1988 г. – М.: Альянс, 2011. – 639 с. 5. Тимофеев, Г.А. Теория механизмов и машин: курс лекций: учеб. пособие для вузов / Г.А. Тимофеев. – М.: Высш. образование, 2009. – 351 с. 6. Методические рекомендации по оформлению выпускных квалификационных работ, курсовых проектов/работ для очной, очно-заочной (вечерней) и заочной форм обучения / сост.: А. Н. Тритенко, О.В. Сафонова. - Вологда: ВоГУ, 2014. – 79 с. 6. Ермолов А.А., Стручков А.П. Теория механизмов и машин: Методическое пособие по выполнению курсового проекта - Рязань: РИ МГОУ, 2002. - 29 с. . 7. Плахтин В.Д., Пантюшин Б.Д. Теория механизмов и машин. Кинематический и силовой анализ плоских механизмов. Основы теории. Курсовое проектирование: Учеб. Пособие. - М: Изд-во МГОУ, 2009. - 94 с. 8. Левитский О.Н., Левитская Н.И. Курс теории механизмов и машин: Учебное пособие для мех. спец. вузов. - 2-е изд., перераб. и доп. - М.: Высш. шк., 1985. - 279 с. 9. Левитский Н.И., Солдаткин Л.П. Теория механизмов и машин: Методические указания и задания на контрольные работы и курсовой проект. - М.: Высш. школа, 1980. - 88 с.  |
