10. Индексы. Тема Индексы Понятие индексов. Их виды Индексы

• Название: Тема Индексы Понятие индексов. Их виды Индексы
• Анкор: 10. Индексы.doc
• Дата: 12.04.2018
• Размер: 225 Kb.
• Имя файла: 10. Индексы.doc
• Тип: Документы; #18005

Тема: Индексы

1. Понятие индексов. Их виды

Индексы  важнейший обобщающий показатель. С их помощью можно измерить динамику соц.-эк. явления за два или более периодов времени, динамику среднего показателя и сопоставить уровни явления в пространстве, по странам, экономическим районам, областям и т. д. Индексы используются для определения степени влияния изменений значений одних показателей на динамику других, а также для пересчета значений макроэкономических показателей из фактических цен в сопоставимые.

Простейший показатель, применяемый в индексном анализе,  индивидуальный индекс, который характеризует изменение во времени или в пространстве отдельных однородных элементов совокупности. Например, индивидуальные индексы физического объема продукции, цен, себестоимости единицы продукции.

В экономических расчетах чаще всего используются сводные, или общие, индексы, которые характеризуют изменение совокупности в целом.

Построение этих индексов является содержанием индексной методологии, в которой сложились две концепции: синтетическая и аналитическая.

Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных явлений, отдельные части которых непосредственно несоизмеримы, и поэтому индексы  показатели синтетические.

В соответствии с аналитической концепцией индексы трактуются как показатели, необходимые для измерения влияния изменения составных частей, факторов сложного явления на изменение уровня этого явления. Поэтому индексной методологией предусматривается определение влияния каждого из факторов путем элиминирования влияния других факторов на уровень изучаемого явления. Такие индексы  показатели аналитические.

Общие индексы строят для количественных и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатную или средневзвешенную.

При построении агрегатного индекса необходимо решить проблему выбора весов, при этом руководствуются следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период; если строится индекс качественного показателя, то используются веса отчетного периода.

В статистической практике, помимо агрегатных, применяются средневзвешенные индексы: среднеарифметический и среднегармонический.

Индексный метод служит также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.

Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующими изменение индексируемого (осредняемого) показателя.

Индекс переменного состава (I_пер.с) для качественных показателей имеет следующий вид:



Величина этого индекса характеризует изменения средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.

Индекс постоянного состава (I_п.с) учитывает изменения только индексируемой величины, показывает средний размер изменения изучаемого показателя у единиц совокупности и выглядит следующим образом:



Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:



Индекс структурных сдвигов (I_{стр.сдв}) характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле:



Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d).

^{В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности Тогда систему индексов можно записать в таком виде:}



Система взаимосвязанных индексов имеет следующий вид:

I_пер.с = I_п.с  I_{стр.сдв.}

При изучении динамики социально-экономических явлений за некоторый интервал времени, включающий в себя более двух периодов времени, используется система индексов: цепные индексы с переменными весами; цепные индексы с постоянными весами, базисные индексы с переменными весами, базисные индексы с постоянными весами.

Для сравнения (сопоставления) показателей в пространстве (по странам, экономическим районам, областям и т. п.) применяются территориальные индексы.

В рыночной экономике особую роль играют индексы цен, которые позволяют оценить динамику цен на товары, измерить инфляцию при макроэкономических исследованиях, пересчитать важнейшие стоимостные показатели системы национальных счетов (СНС) из фактических цен в сопоставимые и др. Для решения различных задач могут быть использованы индексы цен Г. Пааше и Э. Ласпейреса. Весами в индексе Г. Пааше выступает количество продукции текущего периода, а в индексе цен Э. Ласпейреса  количество продукции базисного периода.

Средняя геометрическая из произведения двух агрегатных индексов цен Э. Ласпейреса и Г. Пааше представляет собой индекс цен И. Фишера.

Пересчет в основных стоимостных показателях СНС из фактических цен в сопоставимые осуществляется с помощью индекса-дефлятора. В основе расчета индекса-дефлятора лежит формула Г. Пааше  агрегатная формула с текущими весами. Индекс-дефлятор  индекс цен, применяемый для пересчета какого-либо из стоимостных показателей, выраженных в текущих (действующих) ценах, в базисные цены, то есть цены года, принятого в качестве базисного. С помощью индекса-дефлятора исчисляется динамика физического объема сводных экономических показателей ВНП, фонда потребления, капитальных вложений и другие.

2. Расчет сводного индекса

Рассмотрим методику расчета сводных индексов на конкретном примере. Пример 2.1

Имеются следующие данные о реализации овощной продукции на городском рынке: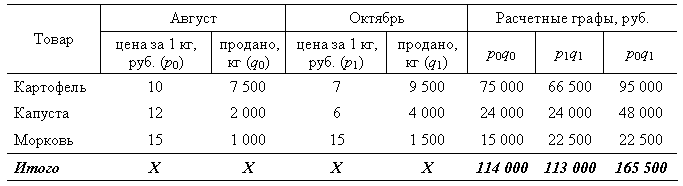



Цены разных товаров, реализуемых в розничной торговле, складывать неправомерно, однако с экономической точки зрения допустимо суммировать их товарооборот. Если сравнивать товарооборот в текущем периоде с его величиной в базисном периоде, то получим сводный индекс товарооборота:



Рассчитаем индекс товарооборота для примера 1:



Мы получим, что товарооборот в целом по рассматриваемой товарной группе в текущем периоде по сравнению с базисным уменьшился на 0,9% (10099,1).

На величину данного индекса оказывает влияние как изменение цен на товары, так и изменение объемов их реализации. Для того чтобы оценить изменение только цен (индексируемой величины), необходимо количество проданных товаров (веса индекса) зафиксировать на каком-либо постоянном уровне. При исследовании динамики таких качественных показателей, как цена, себестоимость, производительность труда, количественный показатель обычно фиксируют на уровне текущего уровня. Таким способом получают сводный индекс цен:



Числитель данного индекса содержит фактический товарооборот текущего периода. Знаменатель же представляет собой условную величину, показывающую, каким был бы товарооборот в текущем периоде при условии сохранения цен на базисном уровне. Поэтому соотношение этих двух категорий и отражает изменение цен. Изменение же количества реализованной продукции не влияет на величину индекса.

Вычислим сводный индекс цен для примера 1:



Следовательно, по данной товарной группе цены в октябре по сравнению с августом снизились на 31,7%.

Числитель и знаменатель сводного индекса цен можно интерпретировать с точки зрения потребителей. Числитель представляет собой сумму денег, фактически уплаченных покупателями за приобретенные в текущем периоде товары. Знаменатель же показывает, какую сумму покупатели заплатили бы за те же товары, если бы цены не изменились. Разность числителя и знаменателя будет отражать величину экономии (если знак «») или перерасхода (если знак «») покупателей от изменения цен:



Третьим индексом в данной индексной системе является сводный индекс физического объема реализации. Он характеризует изменение количества проданных товаров не в денежных, а в физических единицах измерения:



Весами в данном индексе выступают цены, которые фиксируются на базисном уровне.

Индекс физического объема реализации в примере 1 составит:



Физический объем реализации в октябре по сравнению с августом увеличился в 1,45 раза, или на 51 500 руб. (165 500 114 000).

Между рассчитанными индексами существует следующая взаимосвязь: Ip  Iq  Ipq.

Используя взаимосвязь индексов, проверим правильность вычислений : I_pq I_p  I_q  0,683  1,452  0,991, или 99,1%.

Следовательно, снижение товарооборота (на 0,9%) обусловлено ростом объема проданной продукции (на 45,2%) и снижением цен (на 68,3%), что в абсолютном выражении составило 1000 руб. (52 500  51 500).

Мы рассмотрели применение агрегатных индексов в анализе товарооборота цен и физического объема реализации. При анализе результатов производственной деятельности промышленного предприятия приведенные сводные индексы соответственно называются индексом стоимости продукции, индексом оптовых цен и индексом физического объема продукции.

3. Расчет среднеарифметического индекса

Рассмотрим методику расчета среднеарифметического индекса на следующем примере. Пример 3.1

Имеются следующие данные о реализации овощной продукции предприятия розничной торговли округа:



Среднеарифметические индексы чаще всего на практике применяются для расчета сводных индексов количественных показателей, а из качественных показателей  индекс производительности труда Струмилина.

В примере 1 известен розничный товарооборот базисного периода, но отсутствуют данные о товарообороте текущего периода; кроме того, известно изменение физического объема реализации в текущем периоде по сравнению с базисным. В таком случае среднеарифметический индекс физического объема реализации овощной продукции можно рассчитать:



Так как i_qq₀  q₁, формула этого индекса преобразуется в формулу:

Индивидуальные индексы физического объема для примера 1 равны: 0,935; 0,920; 1,015.



Физический объем реализации данных товаров в среднем снизился на 3,6%.

4. Расчет среднегармонического индекса

Рассмотрим методику расчета среднегармонического индекса на следующем примере.Пример 4.1

Имеются следующие данные о реализации отдельных видов товаров предприятия розничной торговли округа:



Среднегармонический индекс рассчитывается в том случае, когда известны только отчетные (текущие) данные, а базисные данные отсутствуют, и известно лишь изменение в процентах или в виде индивидуального индекса.

В примере 1 имеются данные о розничном товарообороте текущего периода, но отсутствуют базисные данные и определены индивидуальные индексы цен по каждой товарной группе, поэтому рассчитаем среднегармонический индекс цен:



Цены по данным товарным группам в текущем периоде по сравнению с базисным в среднем возросли на 1,9%.

5. Расчет индексов средних величин

Рассмотрим методику расчета индексов средних величин на конкретном примере.

Имеются следующие исходные данные о реализации продукции торговыми предприятиями акционерного общества (данные условные):



Вычислим индекс цен переменного состава:



Из таблицы видно, что цена продукции на каждом предприятии в отчетном периоде по сравнению с базисным возросла. В целом же по АО средняя цена снизилась на 2,1% (97,9  100). Это объясняется влиянием изменения структуры реализации продукции по торговым предприятиям, входящим в состав АО. В базисном периоде по более высокой цене продавали продукции в 2 раза больше, в отчетном периоде наоборот увеличился объем продаж продукции по более низкой цене. Рассчитаем индекс структурных сдвигов:



^{Первая часть приведенной формулы позволяет ответить на вопрос, какой была бы средняя цена в отчетном периоде, если бы цены на каждом предприятии сохранились на базисном уровне. Вторая часть формулы отражает фактическую среднюю цену базисного периода.}

Рассчитанный индекс показал, что за счет структурных сдвигов цены снизились на 10,4% (89,6100).

Определим индекс фиксированного или постоянного состава, который не учитывает изменение структуры продаж:



Индекс цен фиксированного состава равен 109,3%, что позволяет сделать следующий вывод: если бы структура продаж продукции по предприятиям АО не изменилась, средняя цена возросла бы на 9,3%. Однако это не произошло, так как влияние структурных сдвигов оказалось сильнее.

Между данными индексами существует следующая взаимосвязь:

Ip^фс  I_ccт  Ip^пс ; 1,093  0,896  0,979.

Задачи и упражнения

1. Имеются следующие данные о реализации мясных продуктов на городском рынке:



Рассчитайте сводные индексы цен, физический объем реализации, товарооборота, а также абсолютную величину перерасхода покупателей от роста цен.

2. Деятельность торговой фирмы за два месяца 2003 г. характеризуется следующими данными:



Оцените общее изменение физического объема реализации с учетом того, что в апреле фирма повысила все цены на 8%.

3. Розничный товарооборот региона в январе 2003 г. характеризуется следующими данными:



Определите сводный индекс цен на потребительские товары.

4. Индекс переменного состава  120%. Под влиянием структурных сдвигов произошло увеличение на 5%. Чему равен индекс, характеризующий изменение средней величины без учета влияния структурных сдвигов?

5. Цены на продукцию возросли на 15%, товарооборот  на 10%. Определите изменение физического объема.

6. Имеются следующие данные о динамике потребления за два полугодия:



Определите общее изменение потребительских цен по всем товарным группам.

7. Строительно-производственная деятельность двух предприятий города характеризуется следующими данными:



Определите:

1) на сколько процентов изменилась средняя цена 1 м² жилья в отчетном году по сравнению с базисным;

2) на сколько долларов изменилась средняя цена 1 м² жилья под влиянием ее изменения на каждом предприятии;

3) на сколько процентов изменилась средняя цена 1 м² жилья под влиянием структурных сдвигов;

4) на сколько тыс. дол. изменилась стоимость вводимого жилья под влиянием изменения средней цены.

Проанализируйте результаты и сделайте выводы.

1. Индексы, их значение в С и классификация. Индексы относятся к важнейшим обобщающим показате­лям изменений. Индекс – от латинского index – указатель, показатель.

Индекс в С - относительный по­казатель, характеризующий изменение величины какого-либо явле­ния (простого или сложного, состоящего из соизмеримых или несо­измеримых элементов) во времени, пространстве или по сравнению с любым эталоном (нормативом, планом, прогнозом и т.д.).

Когда рассматривается сопоставление уровней изучаемого явления во времени, то говорят об индексах динамики, в про­странстве – о территориальных индексах, при сопоставлении с уровнем, например, договорных обязательств – об индексах выполнения обязательств и т.д.

Основным элементом индексного отношения является индексируемая величина-значение признака с/совокупности, изме­нение которой является объектом изучения.

С помощью индексов решаются три главные задачи.

1-индексы позволяют измерять изменение сложных явлений. Напр, требуется установить, насколько увеличился (или уменьшился) в данном году по сравнению с прошлым годом физический объем всей продукции предпри­ятия. Ясно, что продукция разного вида и качества не поддает­ся непосредственному суммированию. Для характеристики из­менения таких сложных явлений во времени применяют индексы динамики. В качестве меры соизмерения (весов) разнородных продуктов можно использовать цену, себестоимость, трудоем­кость продукции и т.д.

2- с помощью индексов можно определить влияние отдельных факторов на изменение динамики сложного явления (напр, влияние изменения уровня цен и изменения количест­ва проданных товаров на объем товарооборота). Используя взаи­мосвязь индексов, можно установить, в какой мере выпуск продук­ции возрос за счет увеличения численности работников и в какой мере – за счет повышения производительности труда.

3- индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нор­мативами, планами, прогнозами. Напр, можно сравнить среднедушевое потребление какого-либо продукта в России и в рзв. странах, а также провести сравнение с нормативом рационального питания.

Индексы классифицируют по трем признакам:

1-По характеру индексируемых величин индексы разделяют:

а)Индексы кол. показателей – индексы физиче­ского объема промышленной и с/х продук­ции, физического объема розничного товарооборота, нац. дохода, потребления продаж ин. валюты и др. Все индексируемые показатели являются объемными, поскольку они характеризуют общий, суммарный размер (объем) того или иного явления и выражаются абсолют­ными величинами. При расчете таких индексов количества оцениваются в сопоставимых ценах.

б)Индексы кач. показателей – индексы курса валют, цен, себестоимости, производительности труда, сред­ней з/п, урожайности и др. Индексируемые показатели этих индексов характеризуют уровень явления в расчете на количественно измеримую единицу совокупности: цена за единицу продукции, себестоимостьединицы продук­ции, выработка в единицу времени (или на одного работника), заработная плата одного работника, урожайность с одного гектара и т.д. Такие показатели называются качественными. Они носят расчетный, вторичный характер. Качественные показатели измеряют не общий объем, а интенсивность, эф­фективность явления или процесса. Как правило, они явля­ются либо средними, либо относительными величинами. Расчет таких индексов производится на базе одинаковых, неиз­менных количеств продукции.

2-По степени охвата единиц совокупности индексы делятся на два класса: индивидуальные и общие.

а)Инд. индексы служат для характеристики измене­ния отдельных элементов сложного явления (напр., измене­ние объёма выпуска телевизоров определенной марки, рост или падение цен на акции в каком-либо АО и т.д.).

б)Общий индекс – отражает изменение всех элементов слож­ного явления. При этом под сложным явлением понимают такую с/совокупность, отдельные элементы которой непо­средственно не подлежат суммированию (физический объем про­дукции, включающей разноименные товары, цены на разные группы продуктов и т.д.).

Если индексы охватывают не все элементы сложного яв­ления, а лишь часть, то их называют групповыми или субиндек­сами (например, индексы продукции по отдельным отраслям промышленности).

Следует подчеркнуть, что С применяет, главным образом, общие и групповые индексы, к-рые и составляют особый прием исследования, именуемый индексным методом. ИМ имеет свою терминологию и символику.

Каждая индексируемая величина имеет обозначение:

q – количество (объем) какого-либо продукта в натураль­ном выражении (от латинского слова quantitas);

р – цена единицы товара ( от латинского слова pretium);

pq – общая стоимость произведенной продукции данного вида или общая стоимость проданных товаров данного вида (товарооборот, выручка);

Чтобы различать, к какому периоду относятся индекси­руемые величины, принято возле символа индекса внизу справа ставить подстрочные знаки: 1 – для сравниваемых (текущих, отчетных) периодов и 0 – для периодов, с которыми производится сравнение. Если изменение явлений изучается за ряд периодов, то каждый из периодов обозначается соответственноподстрочными знаками 0, 1, 2, 3 и т.д.

Инд. индексы обозначаются i и снабжаются подстрочным знаком индексируемого показателя: i_q – инд. индекс объема произведенной продукции отдельного вида или количества (объема) проданного товара данного вида, i_p – инд. индекс цен и т.д.

Общий индекс обозначается буквой I и также сопровождается подстрочным знаком индексируемого показателя: например, I_р общий индекс цен; I_z – общий индекс себестоимости.

Инд. индексы относятся к одному элементу (явлению) и не требуют суммирования данных. Они представ­ляют собой относительные величины динамики, выполнения обя­зательств, сравнения. Выбор базы сравнения определяется це­лью исследования.

Расчет инд. индексов прост, их определяют вычислением отношения двух индексируемых величин:

а) i_p =p₁ / p₀ – инд. индекс цен, где p₁, p₀ единицы продукции в текущем (отчетном) и базисном периодах;

б) i_q = q₁ / q₀ – инд. индекс физического объема продукции.

С аналитической точки зрения индивидуальные индексы аналогичны темпам роста и характеризуют изменения индекси­руемой величины в текущем периоде по сравнению с базис­ным, т.е. во сколько раз она возросла (уменьшилась) или сколько процентов составляет ее рост (снижение). Значения индексов выражают в коэффициентах или процентах. Если из значения индекса, выраженного в процентах, вычесть 100%, т.е. (i–100), то полученная разность покажет, на сколько процентов возросла (уменьшилась) индексируемая величина.

Так, если в I квартале 2000 г. цена 1 л молока на рынке – 15 руб., а во II квартале – 17 руб., то i_p = 17/15 = 1,13, или 113 %, т. е. цена на молоко повысилась на 13 %.

В эк. расчетах для измерения динамики сложного явления чаще всего используются общие индексы. Построение этих индексов и является содержанием индексной методологии.

3- Методика расчета общих индексов сложнее, чем инд., и различна в зависимости от характера индексируе­мых показателей, наличия исходных данных и целей исследования.

Любые общие индексы могут быть построены двумя способами: как агрегатные и как средние из индивидуальных. По­следние в свою очередь делятся на средние арифметические и средние гармонические. Агрегатные индексы качественных пока­зателей могут быть рассчитаны как индексы переменного состава и индексы постоянного (фиксированного) состава. В индексах переменного состава сопоставляются показатели, рассчитанные на базе изменяющихся структур явлений, а в индексах посто­янного состава – на базе неизменной структуры явлений.

Агрегатный индекс является основной формой индекса. Агрегатным он называется потому, что его числитель и зна­менатель представляют собой набор – «агрегат» (от латинского aggregatus – складываемый, суммируемый) непосредственно несоизмеримых и не поддающихся суммированию элементов -сумму произведений двух величин, одна из которых меняется (индексируется), а другая – остается неизменной в числителе и знаменателе (вес индекса). Вес индекса служит для соизмере­ния индексируемых величин.

2. Общие индексы количественных показателей. Типичным индексом количественных показателей являет­ся индекс физического объема. Сложность при построении этого индекса заключается в том, что объемы разных видов продукции и товаров в нату­ральном выражении несоизмеримы и непосредственно сумми­роваться не могут: например, нельзя складывать килограммы хлеба с литрами молока, метрами ткани и парами обуви. Причиной несоизмеримости является неоднородность – различие натуральной формы и свойств.

В связи с этим для разнородных продуктов или товаров сводный индекс физического объема (количества) нельзя по­строить и вычислить как отношение простых сумм: .

Здесь требуется использование специальных приемов ин­дексного метода.

Единство различных видов продукции или разных това­ров состоит в том, что они являются продуктами обществен­ного труда, имеют определенную стоимость и ее денежный соизмеритель – цену р. Каждый продукт имеет также себестоимость z и трудоемкость t. Эти качественные показатели и могут быть использованы в качестве общей меры – коэффици­ента соизмерения разнородных продуктов. Умножая объем про­дукции каждого вида q на соответствующую цену, себестои­мость, трудоемкость единицы продукции, получают сравнимые показатели, которые можно суммировать (qp, qz, qt = Т).

Коэффициенты соизмерения обеспечивают количест­венную сравнимость, позволяют учитывать «вес» продукта в реальном экономическом процессе. Поэтому их показатели-сомножители, связанные с индексируемыми величинами, принято называть весами индексов, а умножение на них – взвешиванием.

Умножая количество произведенной продукции (проданных товаров) на цены (которые, как правило, выступают в качестве соизмерителя неоднородной продукции), получа­ем стоимостное («ценностное») выражение продукции каждого вида, которое допускает суммирование.

Стоимость продукции представляет собой произведение количества продукции в натуральном выражении q на цену единицы продукции р.

Отношение стоимости продукции базисного периода к стоимости продукции текущего периода представляет собой агрегатный индекс стоимости продукции или то­варооборота:

(.1)

Этот индекс показывает, во сколько раз возросла (уменьшилась) стоимость продукции (товарооборота) отчетного периода по сравнению с базисным, или сколько % составляет рост (снижение) стоимости продукции.

Если из индекса стоимости продукции вычесть 100%, то разность (I_pq –100) покажет, на сколько процентов изменилась стоимость продукции в отчетном периоде по сравнению с ба­зисным.

С помощью агрегатных индексов можно рассчитать не только относительное изменение изучаемого явления, но и разложить абсолютный прирост результативного показателя по факторам.

Например:

(2)

где – абсолютный прирост стоимости продукции;

– абсолютный прирост стоимости продукции, обусловленный изменением уровня цен на продукцию;

– абсолютный прирост стоимости продукции, обусловленный изменением физического объема продукции.

Разность числителя и знаменателя формулы (10.1):

показывает, на сколько денежных единиц (рублей) изменилась стоимость продукции в текущем периоде по сравнению с базисным.

При анализе общего объема товарооборота этот прирост объясняется также изменением уровня цен и количества проданных товаров.

Значение индекса стоимости продукции (товарооборота) зависит от двух факторов: изменения количества продукции (объемов) и цен. Для того чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить (элиминировать) в формуле (10.1) влияние другого фактора, зафиксировав его как в числите­ле, так и в знаменателе на уровне одного и того же периода. Так, если продукцию (товары) сравниваемых периодов оцени­вать по одним и тем же, например, базисным ценам р₀, то та­кой индекс отразит изменение только одного фактора – индек­сируемого показателя q и будет представлять собой агрегатный индекс физического объема продукции:

(3) где q₁, q₀ – количество (объем) продукции в натуральном выра­жении в отчётном и базисном периодах соответственно; p₀ – базисная (фиксированная) цена единицы товара.

Индекс физического объема продукции показывает, во сколь­ко раз изменился физический объем продукции или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.

В числителе формулы (10.3) – условная стоимость произведенных в текущем периоде товаров в ценах базисного периода, а в знаменателе – фактическая стоимость товаров, произведенных в базисном периоде.

Разность числителя и знаменателя формулы (3):

показывает, на сколько денежных единиц (рублей) изменилась стоимость продукции в результате роста (уменьшения) ее объема. Прирост физического объема товарооборота объясняется измене­нием количества проданных товаров.

Агрегатный способ исчисления общих индексов в стати­стике является основным наиболее распространенным, вместе с тем применяется и другой способ расчета общих индексов как средних из соответствующих индивидуальных индексов. Средний индекс – это индекс, вычисленный как средняя величина из индивидуальных индексов. К исчислению таких средневзвешенных индексов прибегают тогда, когда имеющаяся в распоряжении информация не позволяет рассчитать общий агрегатный индекс. Так, если неизвестны количества произведенных отдельных видов продукции в нату­ральных измерителях, но известны индивидуальные индексы i_q = q₁ / q₀ и стоимость продукции базисного периода (p₀ q₀), можно определить средний арифметический индекс физического объема продукции.

Исходной базой построения средневзвешенного индекса физического объема продукции служит его агрегатная форма, см. формулу (.3):

Из имеющихся данных можно получить знаменатель этой формулы. Для нахождения числителя используем формулу ин­дивидуального индекса объема продукции i = q₁ : q₀ , из которой следует, что q₁ = i_q  q₀. Подставляя данное выражение в числи­тель агрегатной формы, получаем общий индекс физического объема в форме среднего арифметического индекса физического объема продукции, где весами служит стоимость отдельных ви­дов продукции в базисном периоде (q₀ p₀):(.4)

При выборе весов следует иметь в виду, что средний ин­декс должен быть тождествен агрегатному, который является основной формой индекса.

Если известны данные, позволяющие исчислить только числитель агрегатного индекса физического объема по формуле (10.3), то, аналогично выражая продукцию базисного периода как q₀ = q₁ / i_q, производим замену в знаменателе агрегатной формы. В результате получаем общий индекс физического объ­ема в форме среднего гармонического индекса физического объема, где весами служит стоимость продукции отчетного периода в базисных (или сопоставимых) ценах (q₁ p₀):

(10.5)

В форме СГ взвешенной индекс фи­зического объема используется только в аналитических целях. Следовательно, применение той или иной формулы индекса физического объема (агрегатного, СА или среднего гармонического) зависит от имею­щихся в нашем распоряжении конкретных данных и цели исследования.

3. Общие индексы качественных показателей. Каждый качественный показатель связан с тем или иным объемным показателем, в расчете на единицу которого он ис­числяется. Так, с объемом произведенной (проданной) продук­ции связаны такие качественные показатели, как цена р, себе­стоимость z и трудоемкость t.

В условиях рыночных отношений в экономике особое место среди индексов качественных показателей отводится ин­дексу цен. Поскольку этот индекс характеризует изменение цен, ин­дексируемой величиной в нем будет цена товара. Влияние ко­личества проданных товаров дб устранено, а это возможно только в том случае, если количество продаваемых товаров неизменно в оба периода, т.е. количество товаров од­ного из периодов принято в качестве весов индекса.

Вопрос о том, количество проданных товаров какого перио­да (текущего или базисного) следует взять в качестве весов при построении агрегатного индекса, решают исходя из сферы его применения.

При построении индекса цен в сфере реализации в каче­стве весов индекса обычно берут количество товаров, продан­ных в текущем (отчетном) периоде. Это объясняется тем, что такое исчисление индекса цен позволяет определить не только относительное изменение цен (путем деления числителя индекса на его знаменатель ), но и абсолютную эконо­мию (–) или абсолютный перерасход (+) денежных средств покупателей в результате изменения цен на эти товары (как разность между числителем и знаменателем индекса):



Т.о., агрегатный индекс цен с отчетными веса­ми, предложенный в 1874 г. немецким экономистом Т. Пааше, исчисляют по формуле:

(.6) где – фактическая стоимость товаров (товарооборот) отчетного периода;

– условная стоимость товаров, реализованных в от­четном периоде по базисным ценам.

Рассчитанный по формуле (6) общий индекс цен показы­вает, во сколько раз возрос (уменьшился) в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом.

Если из значения индекса цен I_p вычесть 100%, то раз­ность (I_p–100) покажет, на сколько процентов в среднем воз­рос (уменьшился) за это время уровень цен на массу товаров, реализованную в отчетном периоде.

При таком методе, рассчитав индекс цен по формуле (10.6), можно подсчитать экономический эффект от измене­ния цен.

Между индексами цен, физического объема продукции и стоимости (товарооборота в фактических ценах) существует следующая взаимосвязь:

I_pq = I_p  I_q.

Таким образом, произведение индекса цен на индекс фи­зического объема продукции дает индекс стоимости продукции (товарооборота в фактических ценах), т.е. индексы образуют индексную систему из этих трех индексов.

Если, напр, по определенной группе товаров цена единицы товара в отчетном периоде по сравнению с базисным возросла в среднем на 20 % (I_p=1,20), а физ. объем товарооборота в фиксированных ценах снизился на 5 % (I_q=0,95), то можно определить изменение объема товарообо­рота в фактических ценах: I_pq = 1,20  0,95 = 1,14 или 114%.

Важное место среди индексов цен занимают индексы-дефляторы валового внутреннего продукта.

Дефлятор – это коэффициент, переводящий значение стоимостного показателя за отчетный период в стоимостные измерители базисного. Индекс-дефлятор валового внутреннего продукта для определенного года в общем виде представляет собой отношение стоимости продукции отчетного периода к стоимости объема продукции, структура которого аналогична структуре отчетного года, но определенного в ценах базисного года.

Значения индекса-дефлятора ВВП России (в процентах к предыдущему году):

1996 г. 1997 г. 1998 г. 1999 г.

96,6 100,9 95,1 103,2

4. Индексы средних величин. На динамику качественных показателей, уровни к-рых выражены средними величинами, оказывает влияние изменение структуры изучаемого явления - изменение доли отдель­ных единиц совокупности, из к-рых формируются сред­ние в общей их численности. Так, напр, на среднюю себестоимость какого-либо изделия А может влиять не только изменение себестоимости этого изделия на предприятиях отрасли, но и изменение удельного веса (доли) предприятий с разной себестоимостью в общем выпуске этого изделия. Динамика среднего душевого дохода населения зависит от изменения среднего дохода каждого человека и от изменения количества людей с более высокими (низкими) доходами в общей численности населения.

Следовательно, на изменение среднего значения показателя могут оказывать воздействие одновременно два фактора: изменение значений осредняемого показателя и изменение структуры явления.

Задача состоит в определении степени влияния этих двух факторов на общую динамику средней. Эта задача решается с помощью индексного метода, т.е. путем построения системы взаимосвязанных индексов, в ко­торую включаются три индекса: переменного состава, постоян­ного состава и структурных сдвигов.

Изучение совместного действия этих двух факторов на общую динамику среднего уровня осуществляется в статистике с помощью индекса переменного состава.

Индекс переменного состава представляет собой отношение двух взвешенных средних с изменяющимися (переменными) веса­ми, показывающее изменение индексируемой средней величины.

Для любых качественных показателей х индекс перемен­ного состава можно записать в общем виде: (7) где x₁, x₀ – уровни осредняемого показателя в отчетном и ба­зисном периодах соответственно; f₁, f₀ – веса (частоты) ос­редняемого показателя в отчетном и базисном периодах соответственно.

Чтобы элиминировать влияние изменения структуры совокупности на динамику средней величины, берут отно­шение средних взвешенных с одними и теми же весами (как правило, на уровне отчетного периода). Индекс, характери­зующий динамику средней величины при одной и той же фиксированной структуре совокупности, носит название индекса постоянного (фиксированного) состава и исчисляется в общем виде:

(.8)

После сокращения на формула принимает вид фор­мулы агрегатного индекса качественного показателя:

Индекс постоянного состава показывает, как в отчетном периоде по сравнению с базисным изменилось среднее значение показателя по какой-либо однородной совокупности за счет изменения только самой индексируемой величины, т.е. когда влияние структурного фактора устранено.

Для измерения влияния только структурных изменений на исследуемый средний показатель исчисляют индекс структурных сдвигов как отношение среднего уровня индексируемого показателя базисного периода, рассчитанного на отчетную структуру, к фактической средней этого показателя в базисном периоде: (.9)

Между индексами переменного, постоянного составов и индексом структурных сдвигов существует следующая взаимосвязь: т.е. индекс переменного состава выступает как произведение двух индексов: индекса постоянного состава и индекса структурных сдвигов.

5. Базисные и цепные индексы. Часто в ходе экономического анализа изменение индек­сируемых величин изучают не за два, а за ряд последователь­ных периодов. Следовательно, возникает необходимость по­строения индексов за ряд последовательных периодов, которые образуют индексные системы. Такие системы характеризуют изменения, происходящие в изучаемом явлении в течение ис­следуемого периода времени.

В зависимости от базы сравнения системы индексов бы­вают базисными и цепными.

В системе базисных индексов сравнения уровней индексируемого показателя в каждом индексе производят с уровнем базисного периода, а в системе цепных индексов уровни ин­дексируемого показателя сопоставляются с уровнем предыду­щего периода. Цепные и базисные индексы могут быть как индивиду­альные, так и общие.

Ряды индивидуальных индексов стоимости продукции, физического объема продукции, цен просты по построению. Так, например, обозначив четыре последовательных периода подстрочными индексами 0, 1, 2, 3, исчислим базисные и цеп­ные индивидуальные индексы цен:

а) базисные индексы:

б) цепные индексы:

Между цепными и базисными инд. индексами существует в/связь, позволяющая переходить от одних индексов к другим, – произведение последовательных цепных инд. индексов дает базисный индекс последнего периода:

Отношение базисного индекса отчетного периода к базисно­му индексу предшествующего периода дает цепной индекс отчет­ного периода: