Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение
 Скачать 183.79 Kb. Скачать 183.79 Kb.
|
2.1.46.Исследовать системы линейных уравнений, для совместных систем найти общее и одно частное решение: \( \left\{ \begin{array}{ll} 6x_1+4x_2+5x_3+2x_4+3x_5=1\\ 3x_1+2x_2+4x_3+x_4+2x_5=3\\ 3x_1+2x_2-2x_3+x_4=-7\\ 9x_1+6x_2+x_3+3x_4+2x_5=2 \end{array} \right. \) Приведем расширенную матрицу системы к ступенчатому виду: \( \begin{pmatrix} 6 & 4 & 5 & 2 & 3 & |1 \\ 3 & 2 & 4 & 1 & 2 & |3 \\ 3 & 2 & -2 & 1 & 0 & |-7 \\ 9 & 6 & 1 & 3 & 2 & |2 \end{pmatrix}\ \overset {II-{{I}\over{2}}, III-{{I}\over{2}}, IV-3\times {{I}\over{2}}} {\sim} \begin{pmatrix} 6 & 4 & 5 & 2 & 3 & 1 \\ 0 & 0 & \frac{3}{2} & 0 & \frac{1}{2} & \frac{5}{2} \\ 0 & 0 & \frac{-9}{2} & 0 & \frac{-3}{2} & \frac{-15}{2} \\ 0 & 0 & \frac{-13}{2} & 0 & \frac{-5}{2} & \frac{1}{2} \end{pmatrix}\\ {III+3II, IV+13\{{II}\over{3}} {\sim} \begin{pmatrix} 6 & 4 & 5 & 2 & 3 & 1 \\ 0 & 0 & \frac{3}{2} & 0 & \frac{1}{2} & \frac{5}{2} \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & \frac{-1}{3} & \frac{34}{3} \end{pmatrix}\ \overset {III \leftrightarrow IV} {\sim} \begin{pmatrix} 6 & 4 & 5 & 2 & 3 & 1 \\ 0 & 0 & \frac{3}{2} & 0 & \frac{1}{2} & \frac{5}{2} \\ 0 & 0 & 0 & 0 & \frac{-1}{3} & \frac{34}{3} \\ 0 & 0 & 0 & 0 & 0 & 0 \end{pmatrix}\ \) Значит, количество свободных переменных будет равно 5-3=2 Нужно взять ненулевой минор 3-го порядка: \( \begin{vmatrix} 4 & 5 & 3 \\ 0 & \frac{3}{2} & \frac{1}{2} \\ 0 & 0 & \frac{-1}{3} \end{vmatrix}\ = -2 \) Переменные \( x_2, x_3, x_5 \) - главные переменные. Теперь запишем систему уравнений, соответствующую полученной расширенной матрице: \( \left\{ \begin{array}{ll} 6x_1+4x_2+5x_3+2x_4+3x_5=1\\ \frac {3}{2}x_3+\frac{1}{2}x_5=3\\ \frac{-1}{3}x_5=\frac {34}{3} \end{array} \right. \) Выполним преобразования, оставив главные переменные слева: \( \left\{ \begin{array}{ll} 4x_2+5x_3+3x_5=1-6x_1-2x_4\\ \frac {3}{2}x_3+\frac{1}{2}x_5=3\\ \frac{-1}{3}x_5=\frac {34}{3} \end{array} \right. \) Тогда \( \left\{ \begin{array}{ll} x_2=\frac {-30-6x_1-2x_4}{4}\\ x_3=13\\ x_5=-34 \end{array} \right. \) Общее решение системы: \( (x_1; \frac {-6x_1-2x_4-30}{4}; 13; x_4; -34) \) Одно из частных решений: \( (0; -8; 13; 1; -34) \) 2.2.11Найти решение линейной системы уравнения, используя обратную матрицу и формулы Крамера: Условие: \( \left\{ \begin{array}{crl} x_{1}+2x_{2}+3x_{3}=3 \\ 2x_{1}+6x_{2}+4x_{3}=6 \\ 3x_{1}+10x_{2}+8x_{3}=21 \end{array}\right. \) Решение: Метод обратной матрицы: \( A= \left( \begin{array}{crl} 1 & 2 & 3 \\ 2 & 6 & 4 \\ 3 & 10 & 8 \end{array}\right) B= \left( \begin{array}{crl} 3 \\ 6 \\ 21 \end{array}\right) \\ A^{-1}=\left( \begin{array}{crl} \frac{4}{3} & \frac{7}{3} & \frac{-5}{3} \\ \frac{-2}{3} & \frac{-1}{6} & \frac{1}{3} \\ \frac{1}{3} & \frac{-2}{3} & \frac{1}{3} \end{array}\right) \\ X =A^{-1}\cdot B= \left( \begin{array}{crl} \frac{4}{3} & \frac{7}{3} & \frac{-5}{3} \\ \frac{-2}{3} & \frac{-1}{6} & \frac{1}{3} \\ \frac{1}{3} & \frac{-2}{3} & \frac{1}{3} \end{array}\right) \cdot \left( \begin{array}{crl} 3 \\ 6 \\ 21 \end{array}\right) = \left( \begin{array}{crl} -17 \\ 4 \\ 4 \end{array}\right) \) Метод Крамера: \( \left\{ \begin{array}{crl} x_1 & +2x_2 & +3x_3 & = & 3 \\ 2x_1 & +6x_2 & +4x_3 & = & 6 \\ 3x_1 & +10x_2 & +8x_3 & = & 21 \end{array}\right. \\ \Delta= \left|\begin{matrix} 1 & 2 & 3 \\ 2 & 6 & 4 \\ 3 & 10 & 8 \end{matrix}\right|=6 \\ \Delta_{1}= \left|\begin{matrix} 3 & 2 & 3 \\ 6 & 6 & 4 \\ 21 & 10 & 8 \end{matrix}\right|=-102 \\ \Delta_2= \left|\begin{matrix} 1 & 3 & 3 \\ 2 & 6 & 4 \\ 3 & 21 & 8 \end{matrix}\right|=24 \\ \Delta_3= \left|\begin{matrix} 1 & 2 & 3 \\ 2 & 6 & 6 \\ 3 & 10 & 21 \end{matrix}\right|=24 \\ x_1= \frac{\Delta_1}{\Delta}= \frac{-102}{6}= -17\\ x_2= \frac{\Delta_2}{\Delta}= \frac{24}{6}=4\\ x_3= \frac{\Delta_3}{\Delta}= \frac{24}{6}=4 \) Ответ: x1=−1 x2=4 x3=4 1.3.Решить систему с помощью обратной матрицы и по формулам Крамера: \( \begin{cases} -3x_{1} + 4x_{2} + x_{3} = 17 \\ 2x_{1} + x_{2} - x_{3} = 0 \\ -2x_{1} + 3x_{2} + 5x_{3} = 8 \end{cases} \) Метод Крамера заключается в следующем: составляем матрицу из коэффициентов при неизвестных и находим её определитель, это будет \( \Delta \). Далее, составляем i матриц, в каждой из которых i-ый столбец системы заменяется столбцом свободных членов, находим определитель такой матрицы и это будет \( \Delta_{i} \). Далее согласно формуле \( x_{i} = \frac{\Delta_{i}}{\Delta}\) Запишу систему в матричной форме и вычислю определители с помощью мнемонического правила треугольников: \( \Delta = \left|\begin{array} --3 & 4 & 1 \\ 2 & 1 & -1 \\ -1 & 3 & 5 \end{array}\right| = -53\) \( \Delta_{1} = \left|\begin{array} 117 & 4 & 1 \\ 0 & 1 & -1 \\ 8 & 3 & 5 \end{array}\right| = 96, x_{1} = \frac{-53}{96} = -0.552\) \( \Delta_{2} = \left|\begin{array} --3 & 17 & 1 \\ 2 & 0 & -1 \\ -1 & 8 & 5 \end{array}\right| = -161, x_{2} = \frac{-161}{-53} = 3.037 \) \( \Delta_{3} = \left|\begin{array} --3 & 4 & 17 \\ 2 & 1 & 0 \\ -1 & 3 & 8 \end{array}\right| = 31, x_{3} = \frac{31}{-53} = -0.584 \) Запишем систему в матричной форме: \( A \cdot X = B \), Где \( A = \left(\begin{array}{ccc} -3 & 4 & 1 \\ 2 & 1 & -1 \\ -1 & 3 & 5 \end{array}\right), B = \left(\begin{array}{c} 17 \\ 0 \\ 8 \end{array}\right), X = \left(\begin{array}{c} x_{1} \\ x_{2} \\ x_{3} \end{array}\right) \) Решение системы найдем по формуле \( X= A^{-1} \cdot B \) Обратную матрицу найдём по формуле \( A^{-1} = \frac{1}{|A|} \cdot A^{T} \) \( A^{-1} = \left(\begin{array}{ccc}\frac{-8}{53} & \frac{17}{53} & \frac{5}{53} \\\frac{9}{53} & \frac{14}{53} & \frac{1}{53} \\\frac{-7}{53} & \frac{-5}{53} & \frac{11}{53}\end{array}\right) \) \( A^{-1}\cdot B = X = \left(\begin{matrix}\frac{-96}{53} \\\frac{161}{53} \\\frac{-31}{53}\end{matrix}\right) \) \( x_{1} = \frac{-96}{53}, x_{2} = \frac{161}{53}, x_{3} = \frac{-31}{53} \) 7.2.14.Найти dy и d2y: \( y={(x^2+1)}^3\;Воспользуемся\;формулами:dy=f'(x)dx;\;d^2y=f''(x)\\{(dx)}^2\;dy=y'dx;\;d^2y=y''dx^2;\;\\y={(x^2+1)}^3\\dy=y'dx=3{(x^2+1)}^2\cdot2xdy=6x{(x^2+1)}^2dy\\d^2y=y''dx^2=(6(x^2+1)\cdot2x+3{(x^2+1)}^2\cdot2)dx^2=6(5x^2+1)(x^2+1)dx^2\\Ответ:dy=6x{(x^2+1)}^2dy\\\;\;\;\;\;\;\;\;\;\;\;\;\;d^2y=6(5x^2+1)(x^2+1)dx^2 \) 7.3.24Условие: Найти предел, используя правила Лопиталя: \( \lim \limits_{x \to 0}( x^{tgx} ) \) Решение: \( \lim \limits_{x \to 0}( x^{tgx} ) = 0^{0} \) - неопределенность Для применения правила Лопиталя должна получиться неопределенность \( \frac{0}{0} \) или \( \frac{ \infty }{ \infty } \) Прологарифмируем функцию: \( y= x^{tgx} \) \( lny=ln x^{tgx} \) \( lny=tg x \cdot ln x \) Получим предел: \( \lim \limits_{x \to 0}tgx \cdot lnx= \lim \limits_{x \to 0} \frac{lnx}{ \frac{1}{tgx} } = \frac{ \infty }{ \infty } \) Воспользуемся правилом Лопиталя 2 раза: \( \lim \limits_{x \to a} \frac{f (x) }{g (x) } = \frac{ f' (x) }{ g' (x) } \) \( \lim \limits_{x \to 0} \frac{lnx}{ \frac{1}{tgx} } = \lim \limits_{x \to 0} \frac{ ln' x}{ ( \frac{1}{tgx} ) ' } = \lim \limits_{x \to 0} \frac{ \frac{1}{x} }{ \frac{- tg^{2}x }{ cos^{2}x }} =- \lim \limits_{x \to 0} \frac{ \frac{1}{x} }{ \frac{1}{ cos^{2}x \cdot tg^{2}x } } = - \lim \limits_{x \to 0} \frac{ \frac{1}{x} }{ \frac{ cos^{2}x }{ cos^{2}x \cdot sin^{2}x } } = - \lim \limits_{x \to 0} \frac{ sin^{2}x }{x} = \frac{0}{0} \) \( = - \lim \limits_{x \to 0 } \frac{2sinx \cdot cosx }{1} = 0 \) Чтобы найти ответ нужно экспоненту возвести в полученный ответ: \( e^{0} = 1 \) 1.4.\( Найти\;\frac{dy}{dx},\;\;если\;x=e^{-t}\cdot\cos t,\;y=e^t\cdot\cos t. \) \( Решение:\\Чтобы\;найти\;\frac{dy}{dx},\;необходимо\;вначале\;найти\;производную:y'(x)=\frac{y'_t}{x'_t},где\\y'_t=(e^t\cdot\cos t)'=(e^t)'\cdot\cos t+(\cos t)'\cdot e^t=e^t\cdot\cos t-\sin t\cdot e^t=e^t(\cos t-\sin t);\\x'_t=(e^{-t}\cdot\cos t)'=(e^{-t})'\cdot\cos t+(\cos t)'\cdot e^{-t}=e^{-t}\cdot(-1)\cdot\cos t-\sin t\cdot e^{-t}=-e^{-t}(\cos t+\sin t),\;тогда\\y'(x)=\frac{y'_t}{x'_t}=\frac{e^t(\cos t-\sin t)}{-e^{-t}(\cos t+\sin t)}=\frac{e^{2t}(-\cos t+\sin t)}{(\cos t+\sin t)}=\frac{e^{2t}(\sin t-\cos t)}{(\sin t+\cos t)}\\Отсюда,\;дифференциал\\dy=y'(x)dx,\;тогда\\\frac{dy}{dx}=y'_x=e^{2t}\frac{\sin t-\cos t}{\sin t+\cos t}\\\\Ответ:e^{2t}\frac{\sin t-\cos t}{\sin t+\cos t} \) 11.2.41Вычислить пределы: \( \lim\limits_{{x\to\infty\\y\to 5}} (1+ \frac{3}{x} )^{ \frac{x^2}{x+y}} \) Решение: \( \lim\limits_{{x\to\infty\\y\to 5}} [(1+ \frac{1}{ \frac{x}{3} })^{ \frac{x}{3}} ] ^{ \frac{3}{x}\cdot ( \frac{x^2}{x+y}) } \) Замечательный предел: \( \lim_{t \rightarrow \infty} (1+ \frac{1}{t} )^t=e \) \( e^{\lim\limits_{{x\to\infty\\y\to 5}} \frac{3x^2}{x^2+xy} }=e^{\lim\limits_{{x\to\infty\\y\to 5}} \frac{3x}{x+y} }=e^{\lim\limits_{{x\to\infty\\y\to 5}} \frac{3}{1+ \frac{y}{x} } }=e^{ \frac{3}{1+ \frac{5}{ \infty } \rightarrow0 } }=e^3 \) Ответ: \( e^3 \) 11.3.6.Найти полные приращения данной функции в данной точке \( z=3x^2+xy-y^2+1;M_0(2;1); ∆x=0,01;∆y=0,02. \) Решение. \( x_0=2;y_0=1 \) \( x_0+∆x=x=2,01;y_0+∆y=y=1,02 \) \( M_1(2,01;1,02) \) \( z(M_0)=z(2;1)=3 \cdot2^2+2 \cdot1-2^2+1=14\\ z(x_0+∆;y_0)=z(2,01;1)=3 \cdot2,01^2+2,01 \cdot1-1^2+1=13,1303\\ z(x_0;y_0+∆y)=z(2;1,02)=3 \cdot2^2+21,02-1,02^2+1=13,9996\\ z(M_1)=z(x_0+∆x;y_0+∆y)=z(2,01;1,02)=3 \cdot2,01^2+2,01 \cdot1,01-1,02^2+1=14,1301 \) Таким образом: \( ∆_xz=z(x_0+∆x;y_0)-z(x_0;y_0)=14,1303-14=0,1303\\ ∆_yz=z(x_0;y_0+∆y)-z(x_0;y_0)=13,9996-14=-0,0004\\ ∆z=z(x_0+∆x,y_0+∆y)-z(M_0)=14,1301-14=0,1301 \) Очевидно, что \( ∆z=0,1301 \neq0,1303-0,0004=0,1299=∆_xz+∆_yz \) 11.4.25ЗАДАНИЕ: Найти производную \( y'(x) \) неявной функции, заданной уравнением: \( x^2 \ln y-y^2 \ln x=0 \) РЕШЕНИЕ: Если \( F(x;y) \) - дифференцируемая функция переменных \( x \ и \ y \) в некоторой области \( D \) и \( F'_y(x;y) \neq 0 \), то уравнение \( F(x;y)=0 \) определяет однозначно неявную функцию \( y(x) \), также дифференцируемую, и ее производная находится по формуле: \( y'= \frac{dy}{dx}=- \frac{F'_x(x;y)}{F'_y(x;y)} \) Найдем \( F'_x \ и \ F'_y \) : \( F'_x(x;y)=2x \cdot \ln y - \frac{y^2}{x} \) \( F'_y(x;y)= \frac{x^2}{y}-2y \cdot \ln x \) \( y'=- \frac{2x \cdot \ln y- \frac{y^2}{x} }{ \frac{x^2}{y}-2y \cdot \ln x }=- \frac{(2x^2 \ln y-y^2)y}{(x^2-2y^2 \ln x)x}= \frac{y}{x} \cdot \frac{y^2-2x^2 \ln y}{x^2-2y^2 \ln x} \) При решении воспользовались следующими формулами: \( (x^n)'=nx^{n-1} \\ (\ln x)'= \frac{1}{x} \) \( y'= \frac{dy}{dx}=- \frac{F'_x(x;y)}{F'_y(x;y)} \) ОТВЕТ: \( y'= \frac{y}{x} \cdot \frac{y^2-2x^2 \ln y}{x^2-2y^2 \ln x} \) 11.5.13.Для данных функций найти требуемую частную производную или дифференциал \( \bullet z=x\sin xy+y\cos xy,\ \frac{ \partial^2 z }{ \partial x^2 }\\Вычислим\ частную\ производную\ 1-го\ порядка.\\ \frac{ \partial z }{ \partial x }=(x\ sin\ xy+y\ cos\ xy)'_x=|y=const|=sin\ xy+x\ cos\ xy\cdot y-y\ sin\ xy\cdot y=sin\ xy+xy\ cos\ xy-y^2sin\ xy;\\Вычислим\ частную\ производную\ 2-го\ порядка.\\\frac{ \partial^2 z }{ \partial x^2 }=(sin\ xy+xy\ cos\ xy-y^2sin\ xy)'_x=cos\ xy\cdot y+y\ cos\ xy-xy\ sin\ xy\cdot y-y^2cos\ xy\cdot y=\\=y\ cos\ xy+y\ cos\ xy-xy^2sin\ xy-y^3cos\ xy=\\=2y\ cos\ xy-xy^2sin\ xy-y^3cos\ xy \) 4.7.В полушар радиуса \( R=10 \) вписать прямоугольный параллелепипед наибольшего объема. 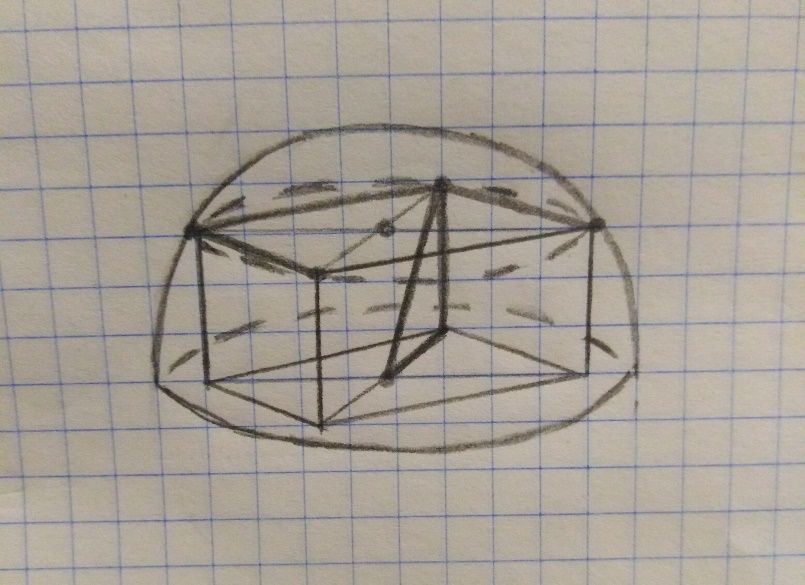 Пусть \( a\ и\ b \) - стороны основания параллелепипеда, \( H \) - высота. Тогда объем параллелепипеда равен \( V=S_{осн}\cdot H=abH \) Верхнее основание параллелепипеда (прямоугольник) вписан в одну из окружностей полушара, следовательно центр данной окружности лежит на пересечении диагоналей основания, то есть в центре прямоугольника. Так как центры всех окружностей полушара лежат на одной линии (перпендикуляре), то центры данной окружности и основания полушара совпадают. Нижнее основание параллелепипеда принадлежит основанию полушара, следовательно их центры также совпадут. Тогда рассмотрим прямоугольный треугольник, одним катетом которого является высота параллелепипеда, другим катетом является половина диагонали основания параллелепипеда, а гипотенузой будет являться радиус полушара (так как она соединяет центр полушара с вершиной параллелепипеда, касающейся шара). Диагональ основания равна \( \sqrt{a^2+b^2} \) Тогда в данном треугольнике \( H^2+\frac{a^2+b^2}{4}=R^2\\ \Rightarrow H=\sqrt{R^2-\frac{a^2+b^2}{4}}=\frac{\sqrt{4R^2-a^2-b^2}}{2} \) Отсюда объем \( V=\frac{ab}{2}\sqrt{4R^2-a^2-b^2} \) Чтобы найти наибольший объем, ищем производные: \(V_a'=\frac{b}{2}\sqrt{4R^2-a^2-b^2}+\frac{ab}{2}\cdot \frac{1}{2\sqrt{4R^2-a^2-b^2}}\cdot (-2a)=\frac{b(4R^2-a^2-b^2)-ba^2}{2\sqrt{4R^2-a^2-b^2}} \) Аналогично \( V_b'=\frac{a(4R^2-a^2-b^2)-ab^2}{2\sqrt{4R^2-a^2-b^2}} \) Решаем систему \( \begin {cases} V_a'=0\\V_b'=0\end {cases} \begin {cases} \frac{b(4R^2-a^2-b^2)-ba^2}{2\sqrt{4R^2-a^2-b^2}}=0\\ \frac{a(4R^2-a^2-b^2)-ab^2}{2\sqrt{4R^2-a^2-b^2}}=0\end {cases} \begin {cases} b(4R^2-a^2-b^2)-ba^2=0\\ a(4R^2-a^2-b^2)-ab^2=0\\4R^2 \neq a^2+b^2 \end {cases} \begin {cases} b(4R^2-2a^2-b^2)=0\\ a(4R^2-a^2-2b^2)=0\\4R^2 \neq a^2+b^2\end {cases} \) \( a\ и\ b \) не могут равняться нулю, тогда \( +\begin {cases} 2a^2+b^2=4R^2\\a^2+2b^2=4R^2 |\cdot (-2) \end {cases} \\2a^2-2a^2+b^2-4b^2=4R^2-8R^2\\4R^2=3b^2\\ b^2=\frac{4R^2}{3}\\\Rightarrow b=\frac{2R}{\sqrt{3}}=\frac{2\cdot 10}{\sqrt{3}}=\frac{20}{\sqrt{3}}\\ a^2=4R^2-2b^2=4R^2-2\cdot \frac{4R^2}{3}=\frac{4R^2}{3}\\ \Rightarrow a=\frac{2R}{\sqrt{3}}=\frac{20}{\sqrt{3}} \) Таким образом \( V=\frac{20}{\sqrt{3}}\cdot \frac{20}{\sqrt{3}}\cdot \frac{1}{2} \cdot \sqrt{4\cdot 10^2-\frac{4\cdot 10^2}{3}-\frac{4\cdot 10^2}{3}}=\frac{200}{3}\sqrt{\frac{4\cdot10^2}{3}}=\frac{4000}{3\sqrt{3}} \) |
