Теорема Пифагора. Исследовательская Работа по Теореме Пифагора. Исследовательская работа по Великая и могущественная Теорема Пифагора Гарипов Артём Денисович
 Скачать 293.02 Kb. Скачать 293.02 Kb.
|
Введение Теорема Пифагора-Теорема имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует зафиксировано около 367 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.) свидетельствует о гигантском числе ее конкретных реализаций, а сама теорема Пифагора звучит так «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов» 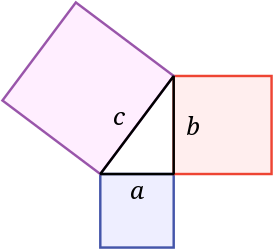 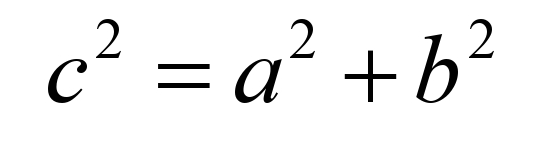 Рис.1 Формула Теоремы Пифагора Теорема, обратная теореме Пифагора-Так-же существует теорема, противоречивая теореме Пифагора, в которой сказано «Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник прямоугольный» 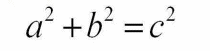 Формула обратная теореме Пифагора Рис.2 I Глава 1: Биография Пифагора О жизни Пифагора известно немного. Он родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии. Родился Пифагор в семье резчика по камню, который сыскал скорее славу, чем богатство. По легенде, отец его, Мнесарх, обратился к Пифии по поводу одной важной для него поездки. Он получил ответ, что поездка будет удачной, а его жена родит дитя, которое будет выделяться среди всех когда-либо живших красотой и мудростью и принесет человеческому роду величайшую пользу на все времена. Мнесарх после предсказания дал своей жене новое имя – Пифаида, а новорожденному – Пифагор. Отец дал ему хорошее образование, обучая его у самых знаменитых учителей того времени. Многие считали, что он сын бога Аполлона. После смерти отца Пифагор отправляется в Милет, где учителями его были Ферекид, Анаксимандр и Фалес. У Ферекида Пифагор получает знания основ музыки и живописи. Единство музыки, поэзии и отточенной мысли, с малых лет усвоенное Пифагором, оказало на его мировоззрение огромное воздействие. Для упражнения памяти Гермадамант заставлял учить песни из «Одиссеи» и «Илиады». Он прививал юному Пифагору любовь к природе и ее тайнам. Пифагор и Египет Пифагор тайно бежит с острова, решив продолжить образование в Египте, этой своеобразной для древних эллинов научной Мекке. Путь был далек и опасен, а все дороги вели через Милет, и здесь юный Пифагор внимательно слушает лекции Фалеса, основателя первой философской школы, тогда уже восьмидесятилетнего старца, и его более молодого коллегу и ученика Анаксимандра, выдающегося географа и астронома. Много важных знаний приобрел Пифагор за время пребывания в Милетской школе, но Фалес советует ему за знаниями продолжить путь в Египет. Перед Египтом Пифагор на некоторое время останавливается в Финикии, где, по преданию, учится у знаменитых сидонских жрецов. Пока Пифагор был в Финикии, Поликрат не только прощает беглеца, но и пишет письмо для Амазиса - фараона Египта. Перед Пифагором открылась неизвестная страна. Его поразило то, что в родной Греции боги были в образе людей, а египетские боги – в образе полу-людей-полуживотных. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки. В Египте проведет он 22 года. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С II большим трудом ему удалось преодолеть эту преграду. Но жизнь его вдруг резко меняется. Скончался фараон Амазис, а его преемник по трону не выплатил ежегодную дань Камбизу, персидскому царю, что послужило поводом для войны. Персы не пощадили даже священные храмы, подверглись гонениям и жрецы, их убивали или брали в плен. Пленен был и Пифагор.  Рис.3 В плену в Вавилоне Наука Вавилона была более развитой, нежели египетская. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений. В плену в Вавилоне Пифагор встречается с персидскими магами, знакомится с учением халдейских мудрецов, со знаниями, накопленными восточными народами за многие века: астрономией, медициной и арифметикой. Изучает восточные религии. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Все это способствует тому, что он сделался одним из самых образованных людей своего времени. Приобщившись к математике, он создает из нее центр своей философской системы. Наиболее поразительными были успехи алгебры. Двенадцать лет пробыл в плену Пифагор, пока его не освободил персидский царь Дарий Гистасп, прослышавший о знаменитом греке. Пифагору уже шестьдесят, и он решает вернуться на родину, чтобы приобщить к накопленным знаниям свой народ. Школа и Пифагор Он переселяется в южную Италию - колонию Греции – Кротон. В Кротоне Пифагор основывает школу - пифагорейский союз, просуществовавший около двух веков и ставший центром духовной и общественной жизни. Желание людей III послушать философа было столь велико, что даже девушки и женщины нарушали закон, запрещавший им присутствовать на собраниях. Одна из них, Феано, становится женой Пифагора. У них рождается трое детей (два сына и дочь), в будущем последователи отца. Свою школу Пифагор создает как тайную организацию со строго ограниченным числом учеников из аристократии, и попасть в нее было не просто. Со временем Пифагор прекращает выступления в храмах и на улицах, а учит уже в своем доме. Система обучения жаждущих знаниями сложная и многолетняя. В этот период проверялось их терпение, скромность. Одна из особенностей школы - почти священное почитание учителя. Только тех, кто прошел многие ступени знаний, Пифагор называет ближайшим учеником и допускает во двор своего дома, где они и ведут беседу. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В школе существовал декрет, по которому авторство всех математических работ приписывалось учителю. Глава 2: Доказательство Теоремы Пифагора Рассмотрим прямоугольный треугольник с катетами a, b и гипотенузой c (рис 4). Докажем, что c²=a²+b²Достроим треугольник до квадрата со стороной a+b так, как показано на (рис 5). Площадь S этого квадрата равна (a+b) ². C другой стороны, этот квадрат составлен из четырёх равных прямоугольных треугольников, площадь каждого из которых равна ½ ab, и квадрата со стороной c, поэтому S=4*½ab+ c²=2ab+ c² 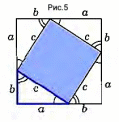 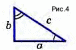 IV Применение Теоремы Пифагора Теорема Пифагора издавна применялась в разных областях науки и техники, в практической жизни. Область применения теоремы достаточно обширна. Применяется в литературе, мобильной связи, архитектуре (индийцы, например, использовали ее для построения алтарей, которые по священному предписанию должны иметь геометрическую форму, ориентированную относительно четырех сторон горизонта), а также в астрономии. Теорема Пифагора была первым утверждением, связавшим длины сторон треугольников. Потом узнали, как находить длины сторон и углы остроугольных и тупоугольных треугольников. Возникла целая наука тригонометрия («тригон» - по-гречески означает «треугольник»). Эта наука нашла применение в землемерии. Но еще раньше с ее помощью научились измерять воображаемые треугольники на небе, вершинами которых были звезды. Сейчас тригонометрию применяют даже для измерения расстояний между космическими кораблями. О теореме Пифагора писали в своих произведениях писатели Плутарх, инженер Витрувий, греческий ученый Диоген, математик Прокл. Не всякое математическое положение удостаивается такого внимания поэтов и писателей. Заключения После изучения построенного материала можно заключить, что теорема Пифагора - одна из самых главных теорем геометрии потому, что с её помощью можно доказать много других теорем и решить множество задач. Пифагор и школа Пифагора сыграли большую роль в усовершенствовании методов решения научных проблем: в математику твёрдо вошло положение о необходимости строгих доказательств, что и придало ей значение особой науки. И несущественно то, что она была известна за много веков до Пифагора, важно то, что Пифагор выделил её, дополнив собственными исследованиями, повысив значимость в мире математических открытий. Теорема применяется в геометрии на каждом шагу. Из неё или с её помощью можно вывести большинство теорем геометрии. Всего известно около 367 различных доказательств теоремы Пифагора. Это говорит о неослабевающем интересе к ней со стороны широкой математической общественности. V Список Литературы и Источников Учебник по Геометрии 7-9класс Авторы: Л.С.Атанасян В.Ф.Бутузов С.Б.Кадомцев Э.Г.Позняк И.И.Тихонова wikipedia ege-ok spacegid |
