проект. в мире графов. Исследовательская работа "В мире графов"
 Скачать 1.31 Mb. Скачать 1.31 Mb.
|
|
Задача 4: Может ли так случиться, что в одной компании из шести человек один человек каждый знаком с двумя и только с двумя другими? Существует два графа соответствующих условию задачи. 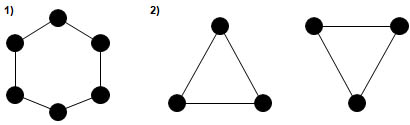 Однако стоит отметить, что во втором варианте получилась не одна, а две компании, где участники одной из них не знакомы с участниками другой. Задача 5: В стране Цифра есть 9 городов с названиями 1, 2, 3, 4, 5, 6, 7, 8, 9. Путешественник обнаружил, что два города соединены авиалинией тогда и только тогда, когда двузначное число, составленное из цифр-названий этих городов, делится на 3. Можно ли из города 1 добраться в город 9? 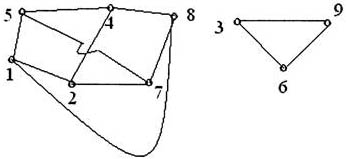 Решение: Покажем возможные маршруты, нарисовав граф. Ответ: нельзя. Задача 6: Дан кусок проволоки длиной 120 см. Можно ли, не ломая проволоки, изготовить каркас куба с ребром 10 см? Какое наименьшее число раз придётся ломать проволоку, чтобы всё же изготовить требуемый каркас? Решение: Нет, нельзя, потому что в кубе вершины представляют собой узлы графа, где сходятся по три ребра. Такие узлы называют "нечетными". Из топологии известно, что нельзя построить граф, не отрывая карандаша от бумаги, если в графе больше двух нечетных узлов. А в кубе - 8 вершин! Задача 7: Задачи о колодцах. Три человека жили в трех домиках, неподалеку от них находились три колодца: один с водой, другой с маслом, а третий с повидлом, и ходили к ним по тропинкам. Однажды эти люди перессорились и решили провести тропинки от своих домов к колодцам так, чтобы эти тропинки не пересекались. Ответ: Это невозможно. Задача 8: Аркадий, Борис. Владимир, Григорий и Дмитрий при встрече обменялись рукопожатиями (каждый пожал руку каждому по одному разу). Сколько всего рукопожатий было сделано? Решение: 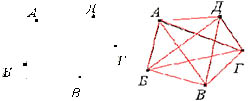 Пусть каждому из пяти молодых людей соответствует определенная точка на плоскости, названная первой буквой его имени, а производимому рукопожатию — отрезок или часть кривой, соединяющая конкретные точки — имена. Если подсчитать число ребер графа, изображенного на рисунке справа, то это число и будет равно количеству совершенных рукопожатий между пятью молодыми людьми. Их 10. Задача 9: В государстве система авиалиний устроена таких образом, что любой город соединён авиалиниями не более чем с тремя другими и из любого города в любой другой можно проехать, сделав не более одной пересадки. Какое максимальное число городов может быть в этом государстве? Решение: 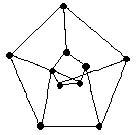 Пусть существует некоторый город А. Из него можно добраться не более, чем до трёх городов, а из каждого из них ещё не более чем до двух (не считая А). Тогда всего городов не более 1+3+6=10. Значит всего городов не более 10. Пример на рисунке (его ещё называют графом Петерсона) показывает существование авиалиний. Задача 10: Дима, приехав из Врунляндии, рассказал, что там есть несколько озёр, соединенных между собой реками. Из каждого озера вытекают 3 реки, и в каждое озеро впадают 4 реки. Докажите, что он ошибается. Решение: Если вытекают 3 реки, а впадают 4 – это невозможно, т. к. количество «втекающих», должно быть равно количеству «вытекающих». Дима не прав. Задача 11: Какие-то две команды набрали в круговом волейбольном турнире одинаковое число очков. Докажите, что найдутся команды А, В и С такие, что А выиграла у В, В выиграла у С, а С выиграла у А. Решение: Пусть А и В набрали одинаковое количество очков, но В выиграла у А, тогда если для любой команды С, у которой выиграла А, выиграла и В, то у В должно быть очков больше, чем у А. Значит, есть такая команда С, что А выиграла у С, а С выиграла у В. Задача 12: В Цветочном городе каждый коротышка знаком с 6 малышками, а каждая малышка – с 6 коротышками. Докажите, что в этом городе число малышек равно числу коротышек. Решение: Если знакомство вида «коротышка – малышка» - это ребро графа, то n – число коротышек, m – число малышек. Тогда всех знакомств (ребер) коротышек 6n, а малышек 6m. Значит 6n= 6m, тогда в этом городе число малышек равно числу коротышек. |
