проект. в мире графов. Исследовательская работа "В мире графов"
 Скачать 1.31 Mb.
|
|
Социограммы (в психологии при исследовании межличностных отношений в группах). Она тоже представлена с помощью графа. (приложение 1 рис.8). 9. Схема железных дорог  Схема железных дорог. Вершины – железнодорожные станции, а рёбра – железнодорожные пути. (приложение 1 рис.9). 10. Созвездия  Графы есть и на картах звездного неба. Это созвездия. (приложение 1 рис.10). 11. Химия. Теория графов позволяет точно определить и пояснить некоторые основные понятия химии: структуру, конфигурацию, конформацию, квантовомеханическое и статистико-механическое взаимодействия молекул, определять число теоретически возможных изомеров органических соединений, позволяет анализировать некоторые химические превращения, описывать химические реакции, определять некоторые свойства молекул. 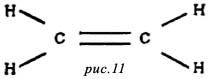 Молекулярный граф — связный неориентированный граф, находящийся во взаимно-однозначном соответствии со структурной формулой химического соединения таким образом, что вершинам графа соответствуют атомы молекулы, а рёбрам графа — химические связи между этими атомам. (приложение 1 рис.11). 12. Математика. Немало поводов для появления графов и в математике. Наиболее очевидный пример – любой многогранник в трёхмерном пространстве. Например, вершины и рёбра куба можно рассматривать как вершины и рёбра графа. При этом мы отвлекаемся от того, как расположены элементы куба в пространстве, оставляя лишь информацию о том, какие вершины соединены рёбрами. На рисунке 12 показаны три способа изобразить один и тот же граф - трёхмерного куба. 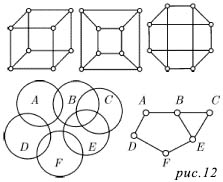 Еще один способ образования графов из геометрических объектов иллюстрирует рисунком 12. Слева показаны шесть кругов на плоскости, а справа - граф, в котором каждая вершина соответствует одному из этих кругов и две вершины соединены ребром. Так же графы под другими названиями проникли в учебники химии, биологии, географии, где они использованы для наглядного и экономного описания различных схем организаций, логических возможностей, классификаций, в том и только том случае, когда соответствующие круги пересекаются. 13. Физика. Одной из наиболее сложных и утомительных задач для радиолюбителей считается конструирование печатных схем. 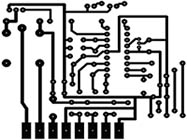 Печатная схема - это пластинка из какого-либо диэлектрика (изолирующего материала), на которой в виде металлических полосок вытравлены дорожки. Пересекаться дорожки могут только в определенных точках, куда устанавливаются необходимые элементы (диоды, триоды, резисторы и другие), их пересечение в других местах вызовет замыкание электрической цепи. Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данного исследования. Перейти к разделу 2.2. Применение графов при решении задач Применение графов при решении задач Пт, 27/01/2017 - 16:15 | nikolay Исследовательская работа: Исследовательская работа "В мире графов" 2.2. Применение графов при решении задач Задачи на вычерчивание фигур одним росчерком Задача 1. О Кенигсбергских мостах. Город Кенигсберг расположен на берегах реки Прегель и двух островах. Различные части города были соединены семью мостами. По воскресеньям горожане совершали прогулки по городу. Вопрос: можно ли совершить прогулку таким образом, чтобы, выйдя из дома, вернуться обратно, пройдя в точности один раз по каждому мосту. Благодаря этой задаче была создана теория графов. 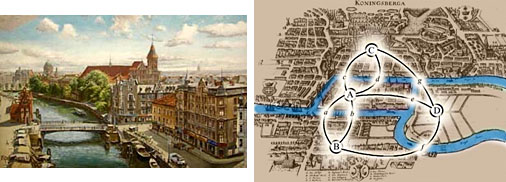 Мосты через реку Прегель расположены как на рисунке. (приложение 2 рис.1). Рассмотрим граф, соответствующий схеме мостов Проблема семи мостов Кёнигсберга. Суть: можно ли пройти по 7 мостам города Кёнигсберга, не ступив на каждый более одного раза. Решение: было найдено русско-немецким математиком Леонардом Эйлером(1736 год). Его рассуждения заключались в следующем: 1) Число нечётных вершин графа должно быть чётно (теорема 2). 2) Если все вершины графа чётные, то можно, не отрывая карандаша от бумаги, начертить граф, при этом можно начинать с любой вершины графа и завершить его в той же вершине. 3) Граф с более чем двумя нечётными вершинами невозможно начертить одним росчерком. 4) Граф кёнигсбергских мостов имел четыре нечётные вершины, следовательно, невозможно пройти по всем мостам, не проходя ни по одному из них дважды. Задача 2. Между 9 планетами Солнечной системы введено космическое сообщение. Ракеты летают по следующим маршрутам: Земля–Меркурий, Плутон–Венера, Земля–Плутон, Плутон–Меркурий, Меркурий–Венера, Уран–Нептун, Нептун–Сатурн, Сатурн–Юпитер, Юпитер–Марс и Марс–Уран. Можно ли добраться с Земли до Марса? 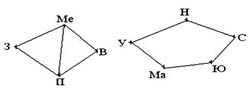 Решение: Нарисуем схему: планетам будут соответствовать точки, а соединяющим их маршруты – не пересекающиеся между собой линии. Ответ: с Земли до Марса добраться нельзя. Логические задачи. Задача 3. В соревнованиях по борьбе, проходящих по олимпийской системе, участвуют 20 борцов. За какое минимальное время можно провести соревнование, если в спортивном зале есть только три борцовских ковра, и на каждую схватку, включая разминку и отдых, отводится час? Изобразите схему соревнований с помощью корневого дерева. 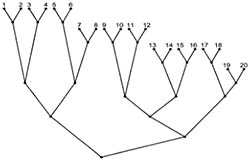 Решение: одна из возможных схем приведена на рисунке. (приложение 2 рис.2) Ответ: На соревнование уйдет 7 часов. Задача 4. Среди девяти монет есть одна фальшивая, которая легче других. Определите ее с помощью двух взвешиваний на рычажных весах. 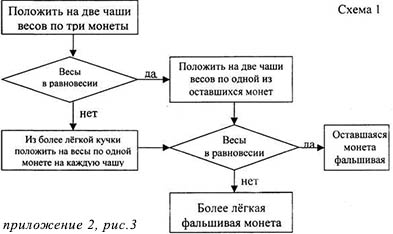 Решение: Разобьем монеты на три группы по три монеты. Положим монеты двух групп на разные чашки весов.Если чашки придут в равновесие, то фальшивая монета — в третьей группе. Если чашки не придут в равновесии, то фальшивая — в более легкой группе. Поиск фальшивой монеты среди троих: положим две монеты на разные чашки весов. Если чашки придут в равновесие, то фальшивая — третья монета. Если чашки не придут в равновесии, то фальшивая — более легкая монета. Решение этой задачи легко изобразить в виде графа-дерева, похожего на алгоритм. (приложение 2, рис.3) Задачи на группу знакомств Задача 5. Однажды Андрей, Борис, Володя, Даша и Галя договорились вечером пойти в кино. Выбор кинотеатра и сеанса они решили согласовать по телефону. Было также решено, что если с кем-то созвониться не удастся, то поход в кино отменяется. Вечером у кинотеатра собрались не все, и поэтому посещение кино сорвалось. На следующий день стали выяснять, кто кому звонил. Оказалось, что Андрей звонил Борису и Володе, Володя звонил Борису и Даше, Борис звонил Андрею и Даше, Даша звонила Андрею и Володе, а Галя звонила Андрею, Володе и Борису. Кто не сумел созвониться и поэтому не пришёл на встречу? 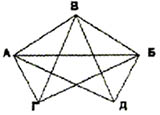 Решение: Нарисуем пять точек и обозначим их буквами А, Б, В, Г, Д. Это первые буквы имён. Соединим те точки, которые соответствуют именам созвонившихся ребят. (приложение 2, рис.4) Задача 6. В первенстве класса по настольному теннису 6 участников: Андрей, Борис Виктор, Галина, Дмитрий и Елена. Первенство проводят по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему моменту некоторые игры уже проведены: Андрей сыграл с Борисом, Галиной, Еленой; Борис – с Андреем, Галиной; Виктор – с Галиной, Дмитрием, Еленой; Галина – с Андреем, Виктором и Борисом. Сколько игр проведено к настоящему моменту и сколько еще осталось? Решение: Получим, что сыграно 7 игр, а осталось – 8. Можно проверить: в графе 6 вершин тогда всего ребер 6*5/2=15 (7+8). Логическая задача на переливание. В ведре 8 л воды, и имеется две кастрюли емкостью 5 и 3 л. Требуется отлить в пятилитровую кастрюлю 4 л воды и оставить в ведре 4 л, т. е. разлить воду поровну в ведро и большую кастрюлю. 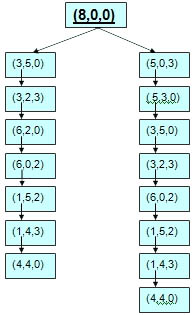 Решение: Ситуацию в каждый момент можно описать тремя числами (приложение рис.16). В результате получаем два решения: одно в 7 ходов, другое в 8 ходов. (приложение 2, рис.5) Задача 7. Имеется шахматная доска 3x3, в верхних двух углах стоят два чёрных коня, в нижних – два белых (рисунок ниже). За 16 ходов поставьте белых коней на место чёрных, а чёрных на место белых и докажите, что за меньшее число ходов это сделать невозможно.  Решение: Развернув граф возможных ходов коней в круг, получим, что в начале кони стояли так, как на рисунке ниже. А в конце кони должны поменяться местами, при этом каждый конь должен сделать 4 хода, а меньшим числом ходов обойтись не удастся, т. к. кони не могут перепрыгивать через друг друга.Тогда, передвигая коней в графе, каждый раз перемещая всех коней, как показано на рисунках 1-4, мы получим за 16 ходов белых коней на месте чёрных, а чёрных на месте белых (рис.5). (приложение 2, рис.6) 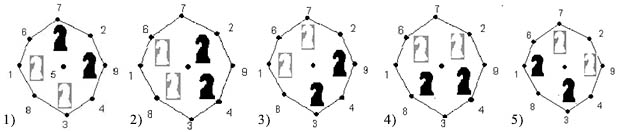 Примеры задач, решаемых методом графов в приложении 3. Перейти к разделу 2.3. Генеалогическое древо – один из способов применения теории графов Генеологическое древо – один из способов применения графов Пт, 27/01/2017 - 17:22 | nikolay Исследовательская работа: Исследовательская работа "В мире графов" 2.3. Генеологическое древо – один из способов применения графов Генеалогическое древо – один из способов применения теории графов. Представьте, что за одним столом собрались несколько больших семей. Каждый гость хочет рассказать о своей семье побольше. Через несколько минут, скорее всего, у слушателей голова пойдет кругом от обилия имен, отчеств, фамилий, дат рождения и другой информации, которой захочется поделиться каждому гостю с собравшимися. И здесь на помощь опять приходят графы. С их помощью можно построить генеалогическое древо, в котором при желании указать всю многочисленную родню до седьмого колена. Деревья – очень удобный инструмент наглядного представления информации самого разного вида. Перейти к разделу 2.4. Описание исследования и составление генеалогического древа моей семьи Описание исследования и составление генеалогического древа моей семьи Пт, 27/01/2017 - 17:31 | nikolay Исследовательская работа: Исследовательская работа "В мире графов" 2.4. Описание исследования и составление генеалогического древа семьи Последовательность действий в исследовании была следующей: 1. Создать модели «Древо жизни» и сетевого графа; 2. Провести опрос родственников (бабушки,тети); 3. Изучить модели составления графов; 4. Создать модели графов. Для результатов исследования мы использовали следующие формы записей: Для интервью: вопросами и ответами на них. Для моделирования: создание рисунков. После проведения исследования я приступил к его первичной обработке, анализу и представлению результатов исследования: 1. Построил образец графа «Древо жизни». 2. Создал графы с помощью полученной информации из интервью. В приложении 4 приведено генеалогическое древо моей семьи. Я ограничился только близкими родственниками, чтобы не перегружать рисунок. 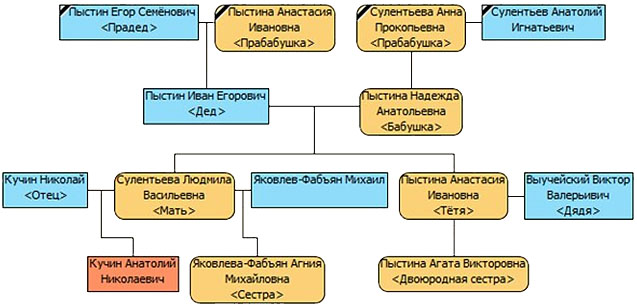 Граф, используемый в генеалогическом древе, не содержит циклов. Заключение. Литература Пт, 27/01/2017 - 17:40 | nikolay Исследовательская работа: Исследовательская работа "В мире графов" Заключение Итак, для того чтобы научиться решать задачи, надо разобраться в том, что собой они представляют, как они устроены, из каких составных частей они состоят, каковы инструменты, с помощью которых производится решение задач. Решая практические задачи с помощью теории графов стало ясно видно, что в каждом шаге, в каждом этапе их решения необходимо применить творчество. С самого начала, на первом этапе, оно заключается в том, что нужно суметь проанализировать и закодировать условие задачи. Второй этап – схематическая запись, которая состоит в геометрическом представлении графов, и на этом этапе элемент творчества очень важен потому, что далеко не просто найти соответствия между элементами условия и соответствующими элементами графа. Решая транспортную задачу или задачу на составление генеалогического дерева я сделал вывод, что безусловно метод графов интересен, красив и нагляден. Я убедился, что графы достаточно широко применяются в экономике, управлении, технике. Также теория графов применяется в программировании. Об этом в данной работе не шла речь, но думаю, что это только вопрос времени. В моей исследовательской работе по математике на тему "В мире графов" рассмотрены математические графы, области их применения, решено несколько задач с помощью графов. Знание основ теории графов необходимо в различных областях, связанных с управлением производством, бизнесом (например, сетевой график строительства, графики доставки почты). Кроме того, работая над работой, я освоил работу на компьютере в текстовом редакторе WORD. Таким образом, задачи исследовательской работы выполнены. Итак, из всего вышесказанного неопровержимо следует практическая ценность теории графов, доказательство которой и являлось целью данной работы. Использованная литература 1. Берж К. "Теория графов и ее применение", М., ИЛ, 1962г. 2. Гарднер М., Оре О. "Графы и их применения", М. "Мир", 1965г. 4. Зыков А.А. "Теория конечных графов", Новосибирск, "Наука", 1969г. 4. Ю. Нестеренко, С. Олехник, М. Потапов “Лучшие задачи на смекалку”. 5. Ресурсы сети Интернет. Перейти к разделу: Приложения Приложения Пт, 27/01/2017 - 23:14 | nikolay Исследовательская работа: Исследовательская работа "В мире графов" Изображения из Приложения 1, Приложения 2 и Приложения 3 распределены в тексте работы при публикации! Приложение 3 Задачи с применением графов Задача 1: В классе 30 человек. Может ли быть так, что 9 человек имеют по 3 друга, 11 – по 4 друга, а 10 – по 5 друзей? Ответ: Нет, так как 9+10=19 и это нечетное число (смотри теорему 2). Задача 2: Как вы помните, охотник за мертвыми душами Павел Иванович Чичиков побывал у известных вам помещиков по одному разу у каждого. Он посещал их в следующем порядке: Манилова, Коробочку, Ноздрева, Собакевича, Плюшкина, Тентетникова, генерала Бетрищева, Петуха, Констанжогло, полковника Кошкарева. Установите, какое имение кому принадлежит, если ни по одной из дорог Чичиков не проезжал более одного раза. 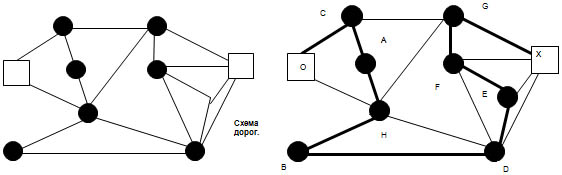 Рассмотрим схему: к A и B идут всего две дороги, поэтому отмечаем их. Значит, Чичиков обязательно должен был проехать по OC. Отмечаем BD. Чтобы посетить E, но также попасть в G, существует единственный маршрут. Итого получается A – Ноздрев, B – Плюшкин, C – Коробочка,D –Тентетников,E – Бетрищев, F – Петух, G – Констанжогло, H – Собакевич, O – Манилов,X – Кошкарев. Задача 3: В автомобильных гонках Коля, Боря, Юра заняли первые четыре места. На вопрос, какие места они заняли, трое из них ответили: 1) Коля ни первое, ни четвертое; 2) Боря второе; 3) Вова не был последним. Какое место занял каждый мальчик? 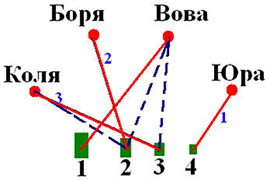 Ответ: 1 – Вова; 2 – Боря; 3 – Коля; 4 – Юра. |