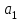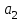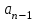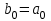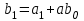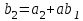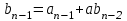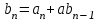Схема Горнера и её применения. Исследовательская работа Выполнена обучающейся 10 класса моу Звениговский лицей Городиловой Анастасией Павловной
 Скачать 209.96 Kb. Скачать 209.96 Kb.
|
|
Схема Горнера и её применения Исследовательская работа Выполнена обучающейся 10 класса МОУ «Звениговский лицей» Городиловой Анастасией Павловной Научный руководитель: Тихонов Николай Иванович, учитель математики высшей категории МОУ «Звениговский лицей» г. Звенигово, 2020 Оглавление
Введение Увлечение математикой начинается с размышления над какой-то интересной задачей или проблемой. Любому завороженному математическими тайнами человеку интересно знать историю математических открытий, разные способы решения задач, уметь использовать математические теоремы для решения сложных задач. Я, Городилова Анастасия, обучающаяся МОУ «Звениговский лицей» в 9 классе на уроках математики изучала тему «Многочлены». Находила значения многочленов в заданной точке, делила многочлены, находила корни многочленов. Если говорить вообще о многочленах, то следует отметить, что в необозримом царстве функций многочлены занимают, на первый взгляд, очень скромное место. Однако это первое впечатление обманчиво. Оказывается, что вычислять многочлены приходится часто, а значит важно научиться делать это как можно проще. Известно, что при работе с многочленами, приходится сталкиваться с необходимостью проводить большое количество всевозможных вычислений. Кроме того, существует немалая вероятность возникновения вычислительных ошибок, так, например, при расчете корней многочлена необходимо отработать большое количество вариантов при подборе значений, которые действительно будут корнями. На уроках математики мы изучили схему Горнера, которая позволяет находить значение многочлена и его корни. Обучаясь в 10 классе, я снова столкнулась с задачами, для решения которых можно или нужно применять схему Горнера. На курсах для подготовки к ЕГЭ по математике, при решении некоторых уравнений с параметром снова пригодились знания, полученные при изучении многочленов в 9 классе. Мы, с моим преподавателем, решили выяснить спектр основных задач, при решении которых применяется схема Горнера. Так как, считаем, что эта тема является актуальной в школьном курсе математики, которая: Позволяет находить значение многочлена и его корни, не выполняя громоздких вычислений; Позволяет решать уравнения и неравенства высших порядков не способом группировки многочленов, а более рациональным путем, экономящим время; Применяется при умножении многочлена на одночлен 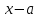 ; ; Используется при сокращении алгебраических дробей: Применяется для решения задач с параметром. Мы определили: Объект исследования: Схема Горнера и её применения. Предмет исследования: Задачи, решаемые при помощи схемы Горнера. Методы исследования: моделирование, сравнение, обобщение, аналогии, изучение литературных и Интернет-ресурсов, анализ и классификация информации. Основная цель исследования заключается в выяснении многообразия задач, которые можно решить, используя схему Горнера. Для достижения поставленной цели предусматриваем решение следующих задач: Изучить схему Горнера, подобрав необходимую литературу; Отобрать материал для исследования; Проанализировать и систематизировать полученную информацию. Основная часть 1. Горнер Вильямc Джордж. Горнер Вильямc Джордж (1786-22.9.1837)-английский математик. Родился в Бристоле. Учился и работал там же, затем в школах Бата. Основные труды по алгебре. В 1819г. опубликовал способ приближенного вычисления вещественных корней многочлена, который называется теперь способом Руффини-Горнера (этот способ был известен китайцам еще в XIII в.) Именем Горнера названа схема деления многочлена на двучлен х-а. 2. Этье́н Безу́. Этье́н Безу́ — французский математик, член Французской академии наук (1758).Преподавал математику в Училище гардемаринов (1763) и Королевское артиллерийском корпусе (1768).Основные его работы относятся к алгебре (исследование систем алгебраических уравнений высших степеней, исключение неизвестных в таких системах и др.). Автор шеститомного «Курса математики» (1764—1769), неоднократно переиздававшегося. 3. Теорема Безу. Схема Горнера Одним из способов решения уравнений высших степеней является способ разложения на множители многочлена, стоящего в левой части уравнения. Этот способ основан на следующем применении теоремы Безу. Если число a является корнем многочлена P(x),имеющего степень n, то этот многочлен можно представить в виде  p(x)=(x-a)Q(x), где Q(x)-частное от деления P(x) на x-а , многочлен степени n-1. Таким образом, если известен хотя бы один корень уравнения P(x)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени n-1,т.е., как говорят, понизить степень уравнения. p(x)=(x-a)Q(x), где Q(x)-частное от деления P(x) на x-а , многочлен степени n-1. Таким образом, если известен хотя бы один корень уравнения P(x)=0 степени n, то с помощью теоремы Безу можно свести задачу к решению уравнения степени n-1,т.е., как говорят, понизить степень уравнения. Возникает естественный вопрос: как найти хотя бы один корень уравнения? В случае уравнения с целыми коэффициентами можно отыскать рациональные, в частности целые корни, если, конечно, они существуют. Способ отыскания рациональных корней алгебраического уравнения с целыми коэффициентами дается следующей теоремой. Пусть несократимая дробь 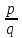 является корнем уравнения является корнем уравнения 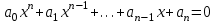 с целыми коэффициентами. Тогда число p является делителем свободного члена 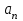 , а q-делителем старшего коэффициента , а q-делителем старшего коэффициента 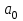 . .Cледствие1. Любой целый корень уравнения с целыми коэффициентами является делителем его свободного члена Cледствие2. Если старший коэффициент уравнения с целыми коэффициентами равен 1 ,то все рациональные корни уравнения, если они существуют, целые. Понижение степени уравнения p(x)=0 в случае, когда известен его корень a, сводится к нахождению частного от деления p(x) на x-a деление многочлена 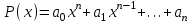 На двучлен x-a удобно выполнять по так называемой схеме Горнера. Вычисление коэффициентов многочлена Q(x) и остатка 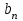 записывают в виде следующей таблицы: записывают в виде следующей таблицы:
Она называется схемой Горнера. В первой строке этой таблицы записаны коэффициенты многочлена P(x). Во второй получаются коэффициенты частного и остаток. Старший коэффициент частного равен старшему коэффициенту делимого. Если уже заполнено несколько клеток второй строки ,то следующая пустая клетка заполняется так: берут стоящее над ней число первой строки и прибавляют к нему произведение a и предыдущего элемента второй строки . В последней клетке второй строки под свободным членом делимого получается остаток от деления 4. Применение схемы Горнера 4.1 Нахождение значения функции в точке Так как по теореме Безу 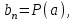 то схема Горнера позволяет находить значение многочлена (функции) то схема Горнера позволяет находить значение многочлена (функции) 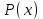 при при 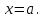 Во многих случаях вычисление по схеме Горнера удобнее, чем непосредственная подстановка Во многих случаях вычисление по схеме Горнера удобнее, чем непосредственная подстановка 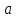 в многочлен в многочлен 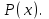 Задача 1 . Найти значение функции 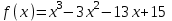 в точке х = -1, в точке х = -1,Составим таблицу, в первой строке которой записаны коэффициенты многочлена 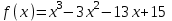 . .
f(-1)=24(мы нашли значение функции в точке -1) Задача 2 . Вычислить p(3) ,где 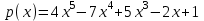
Значит, p(3)=535. 4.2 Разложение многочлена на множители Для нахождения корня многочлена нам помогут следующие теоремы: Теорема 1: Если сумма коэффициентов многочлена равна 0, то число 1 является корнем многочлена. Теорема 2: Если сумма коэффициентов, стоящих на чётных местах равна сумме коэффициентов, стоящих на нечётных местах, то число (-1) является корнем многочлена. Задача 1. Разложить на множители с целыми коэффициентами многочлен 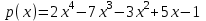 Решение: Ищем целые корни среди делителей свободного члена: 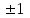 . . Составим таблицу коэффициентов и выясним, является ли число 1 корнем многочлена?
По схеме Горнера заполним пустые ячейки таблицы.
Так, как в последней ячейке получилось значение равное нулю, то х = 1 – это корень многочлена. Или это следует из Теоремы 1. Из теоремы Безу следует, что 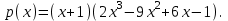 Ищем целые корни многочлена 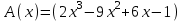 среди делителей его свободного члена: среди делителей его свободного члена: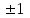 . Вычисления показывают, что целых корней нет. Так как старший коэффициент многочлена не равен 1,то многочлен может иметь дробные рациональные корни. Дробными корнями могут быть только числа . Вычисления показывают, что целых корней нет. Так как старший коэффициент многочлена не равен 1,то многочлен может иметь дробные рациональные корни. Дробными корнями могут быть только числа 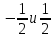 . Подходит . Подходит 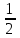 Имеем: 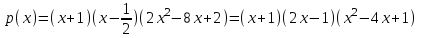 Трехчлен 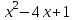 на множители с целыми коэффициентами не раскладывается. на множители с целыми коэффициентами не раскладывается.Ответ: 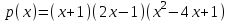 10.3 Деление многочленов Задача 1. Разделить многочлен 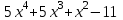 на на 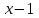 , используя схему Горнера. , используя схему Горнера.Запишем данный многочлен в виде 5х4 + 5х3 + х2 + 0х – 11 и составим таблицу. При помощи схемы Горнера её заполним.
Числа, расположенные во второй строке, есть коэффициенты многочлена, полученного после деления на х-1. Т.к. степень исходного многочлена 5х4+5х3+х2-11 равнялась четырем, то степень полученного многочлена на единицу меньше, т.е. равна трем. Получаем 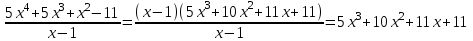 В нашем случае остаток равен нулю. Значит, можно сформулировать такой вывод: многочлен делится на х-1, и еще х = 1 является корнем многочлена. 10.4 Решение уравнений высших степеней Уравнение вида Р(х)=0, где Р(х) - многочлен степени n > 2, записанное в виде a0 xn + a1 xn-1 + a2 xn-2 +…+an-1 x +an = 0, называют уравнениями высших степеней, где n показывает степень уравнения. Задача 1. Решить уравнение: 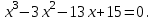
Коэффициент перед старшей степенью переменной (т.е. перед x3) равен единице. В этом случае целочисленные корни многочлена нужно искать среди делителей свободного члена, т.е. среди делителей числа 15. Свободный член 15: его делители ± 1, ± 3, ± 5, ± 15 По теореме 1, сумма коэффициентов равна 0, значит 1 является корнем. Составим таблицу из двух строк: в первой строке запишем коэффициенты многочлена 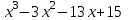 , расположенные по убыванию степеней переменной х. Во второй строке запишем 1, т.к. мы делим на х-1. , расположенные по убыванию степеней переменной х. Во второй строке запишем 1, т.к. мы делим на х-1.Начнем заполнять пустые ячейки во второй строке. Во вторую ячейку второй строки запишем число 1, просто перенеся его из соответствующей ячейки первой строки. Следующую ячейку заполним по такому принципу: 1⋅1+(-3)=-2. Аналогично заполним и четвертую ячейку второй строки: 1⋅(-2)+(-13)=-15 Для пятой ячейки получим: 1⋅(-15)+15=0. Значит 1 корень уравнения. Если получается число, отличное от нуля, то это не корень. Заполняем таблицу и для других делителей:-1 не удовлетворяет по теореме 2, поэтому не проверяем. Из таблицы видно, что найдены три корня. Уравнение 3 степени не может иметь более трех корней, поэтому остальные делители можно не проверять. Мы нашли корни уравнения х1 =1, х2= -3, х3 = 5 Ответ: -3; 1; 5. Задача 2. а) Найти целые корни уравнения 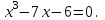 Если уравнение имеет целые корни, то они находятся среди делителей свободного члена. Запишем эти делители: ± 1, ± 2, ± 3, ± 6. Составим и заполним таблицу по схеме Горнера. Для начала запишем многочлен в стандартном виде: х3- 0х2 - 7х-6. 1 не подставляем, т.к. не выполняется условие теоремы 1.
решив уравнение получили корни х1 = -1, х2 = -2, х3 = 3 10.5 Умножение многочлена на одночлен 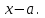 Схему Горнера можно использовать не только для разложения многочлена на множители, но и для решения обратной задачи – для умножения многочлена 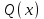 на двучлен на двучлен 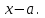 Пример1. Преобразовать в многочлен стандартного вида произведение 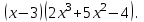 Решение. При 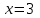 искомый многочлен обращается в нуль. Если бы мы искали значение многочлена с помощью схемы Горнера, то вторая строка таблицы содержала бы коэффициенты многочлена искомый многочлен обращается в нуль. Если бы мы искали значение многочлена с помощью схемы Горнера, то вторая строка таблицы содержала бы коэффициенты многочлена 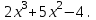 Учитывая, что его коэффициент при Учитывая, что его коэффициент при 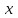 равен нулю, начертим таблицу и заполним её вторую строку. равен нулю, начертим таблицу и заполним её вторую строку.
В первой клетке первой строки должно стоять число 2. Во второй клетке – число, которое в сумме с произведением 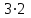 даёт 5, т.е. число -1. Число в третьей клетке первой строки в сумме с произведением даёт 5, т.е. число -1. Число в третьей клетке первой строки в сумме с произведением 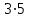 даёт 0. Значит, это число -15. Аналогично, в четвёртой клетке должно стоять число -4, а в последней, пятой клетке первой строки – число 12. Заполним верхнюю строку таблицы. даёт 0. Значит, это число -15. Аналогично, в четвёртой клетке должно стоять число -4, а в последней, пятой клетке первой строки – число 12. Заполним верхнюю строку таблицы.
В верхней строке таблицы мы получили коэффициенты искомого многочлена. Ответ: 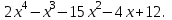 4.6 Решение неравенств высших степеней. Пример1. Решите неравенство 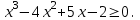 Для решения неравенства методом интервалов разложим на множители многочлен 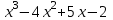 . Так, как сумма его коэффициентов равна 0, то один из корней равно 1. . Так, как сумма его коэффициентов равна 0, то один из корней равно 1.Составим таблицу и заполним её по схеме Горнера.
По теореме Безу получаем 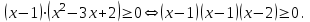 Далее 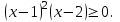 Решив последнее неравенство методом интервалов, получим, что 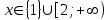 . .Ответ: 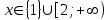 . .10.7 Применение схемы Горнера при решении задач с параметром. 1) Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых х0 , если f(х) = х3 + 8х2 + ах + b, х0 = – 3. Так один из корней х0 = – 3 , то по схеме Горнера имеем:
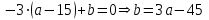 х3 + 8х2 + ах + b = (х + 3) (х2 + 5х + (а – 15)) Уравнение х2 + 5х + (а – 15) = 0 должно иметь два корня. Это выполняется только в том случае, когда D > 0. а = 1; b = 5; с = (а – 15), D = b2 – 4ac = 25 – 4 (a – 15) = 25 + 60 – 4a > 0, 85 – 4a > 0; 4a < 85; a < 21 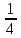 Наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три корня, а = 21. Ответ: 21. 2) Многочлен 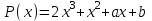 при делении на при делении на 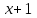 , даёт остаток 18, , даёт остаток 18, а на 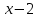 делится без остатка. Найдите значения делится без остатка. Найдите значения 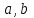 и корни многочлена. и корни многочлена.Решение. Если многочлен 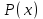 делится на делится на 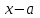 с остатком, равным 18, с остатком, равным 18, то из теоремы следует, что 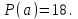 В нашем примере получается, что 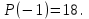 Так, как Так, как 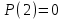 , то , то 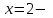 корень многочлена. корень многочлена.Вычислим 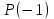 и и 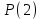 по схеме Горнера. по схеме Горнера.Для 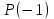 : :
Для 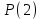 : :
Из таблиц следует: 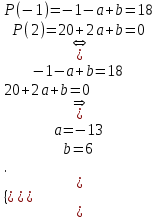 Запишем многочлен 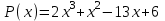 . Зная его корень . Зная его корень 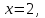 разложим на множители. разложим на множители.Таблица:
Итак, 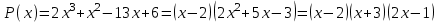 . .При 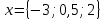 многочлен равен 0. Значит его корни многочлен равен 0. Значит его корни 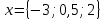 . .Ответ: 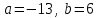 и и 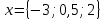 . .5. Результаты исследования. В ходе исследования мы получили следующие результаты: При помощи схемы Горнера можно: Находить значение многочлена и его корни, не выполняя громоздких вычислений; Решать уравнения и неравенства высших порядков не способом группировки многочленов, а более рациональным путем, экономящим время; Умножать многочлен на одночлен 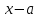 ; ; Сокращать алгебраические дроби: Решать задачи с параметром. Мы расширили свои знания о решении задач при помощи схемы Горнера; Определили для себя классификацию исследуемых задач, убедились в их многообразии. Заключение. В ходе работы я повторила, как разложить многочлен на множители, делить многочлен на многочлен, умножить многочлен на одночлен, решать уравнения и неравенства высших степеней и находить значения функции в точке, не выполняя громоздких вычислений. В этом учебном году научилась решать задачи с параметром, решение которых можно реализовать при помощи схемы Горнера. Дальнейшая моя задача, научиться эффективно использовать схему Горнера для решения уравнений и неравенств высших степеней из тестов ЕГЭ по математике профильного уровня. Теперь я овладела основными методами решения различных уравнений высших степеней, для n>2. Меня эта тема и такой подход к решению уравнений очень заинтересовал, но единственный минус это то, что схема работает только для рациональных корней. Я пришла к выводу, что тема, которая меня заинтересовала, достаточно многогранна, задачи решаемые при помощи схемы Горнера многообразны, методы и приёмы их решения также разнообразны. Поэтому я решила продолжить работу в этом направлении: особенно интересными показались мне задачи с параметром. Считаю, что наша исследовательская работа имеет большое практическое применение. Результаты работы можно использовать на занятиях олимпиадных групп по математике и при подготовке к ЕГЭ по математике профильного уровня. Считаю, что цели и задачи данной работы полностью реализованы. Список использованных источников литературы Алгебра. 9 кл.:учебник/Г.К. Муравин, К.С. Муравин, О.В. Муравина. – 4-е изд.., стереотип. – М.:Дрофа,2017. – 319,[1]с. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. Углублённый уровень. 10 класс: учебник / Г.К. Муравин, О.В. Муравина.-5-е изд., стереотип.-М.:Дрофа, 2018.-285 ,[1]с. Углублённое изучение алгебры и математического анализа: Метод. Рекомендации и дидакт.материалы: Пособие для учителя / М.Л. Галицкий, М.М. Мошкович, С.И. Шварцбурд.-3-е изд., дораб.-М.: Просвещение,1997.-352с. –ISBN 5-09-006592-6. https://ru.wikipedia.org/wiki/Горнер,_Уильям_Джордж 5. https://ru.wikipedia.org/wiki/Теорема_Безу Приложение. Задачи для самостоятельного решения. Задание 1. Найти значение функции в указанной точке. А) 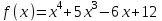 , в точке -7 , в точке -7Б) 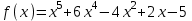 , в точке 12 , в точке 12В) 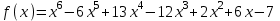 , в точке 37 , в точке 37Г) 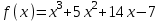 , в точке 24 , в точке 24Задание 2. Разложить на множители с целыми коэффициентами А) 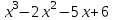 Б) 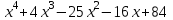 В) 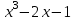 Г) 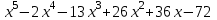 Задание 3. Сократить дроби: А) 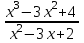 Б) 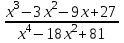 В) 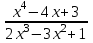 Г) 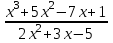 Задание 4. Решить уравнение А) 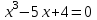 Б) 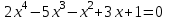 В) 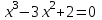 Г) 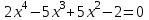 Задание 5. Преобразовать в многочлен стандартного вида произведение: А) 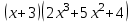 Б) 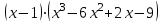 В) 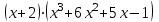 Г) 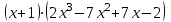 Задание 6. Решение неравенств высших степеней. А) 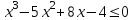 Б) 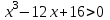 В) 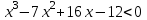 Г) 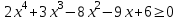 Задание 7. Найдите наибольшее целое значение параметра а, при котором уравнение f(х) = 0 имеет три различных корня, один из которых х0 , если: f(x) = x3 – 2x2 + ax + b, x0 = – 1 f(x) = x3 + 11x2 + ax + b, x0 = – 4 f(x) = x3 – 11x2 + ax + b, x0 = 4 f(x) = x3 – 13x2 + ax + b, x0 = 4 Задание 8. При каких значениях 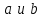 многочлен многочлен 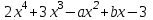 делится без остатка на делится без остатка на 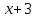 , а при делении на , а при делении на 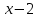 даёт остаток, равный 5? даёт остаток, равный 5? Задание 9. При каких значениях 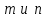 многочлен многочлен 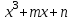 делится без остатка на трёхчлен делится без остатка на трёхчлен 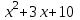 ? ?Задание 10. При каких значениях 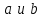 многочлен многочлен 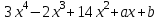 при делении на при делении на 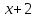 даёт остаток, равный 101, a на даёт остаток, равный 101, a на 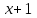 делится без остатка? делится без остатка? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||