фильтр калмана в матлаб. пример фильтра калмана. Исследуется модель объекта управления в виде
 Скачать 220.74 Kb. Скачать 220.74 Kb.
|
|
Постановка задачи. Исследуется модель объекта управления в виде 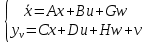 с известными входами u и возмущениями по входам w и измерениям ν, которые являются «белым» шумом со следующими характеристиками (М – математическое ожидание): M{w} = M{v} = 0 M{w(t)w(τ)T} = Q δ(t – τ) M{v(t)v(τ)T} = R δ(t – τ) M{v(t)w(τ)T} = N δ(t – τ) Требуется выполнить синтез наблюдателя для оценивания вектора переменных состояния объекта, который минимизирует установившуюся ошибку оценивания 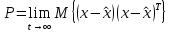 Оптимальным решением является фильтр Калмана, описываемый уравнениями 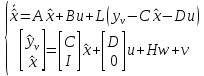 где матрица коэффициентов обратных связей L определяется на основе решения алгебраического матричного уравнения Риккати. Наблюдатель (рис. 1) объединяет фильтр Калмана и объект управления. Наблюдатель использует известные входы u и результаты измерений yv, искаженные случайными помехами, для того, чтобы вычислить оценки вектора переменных состояния 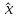 и выходов и выходов 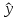 . .Для синтеза фильтра Калмана используем функцию Control System Toolbox: [kest, L, P] = kalman(sys, Qn, Rn, Nn) 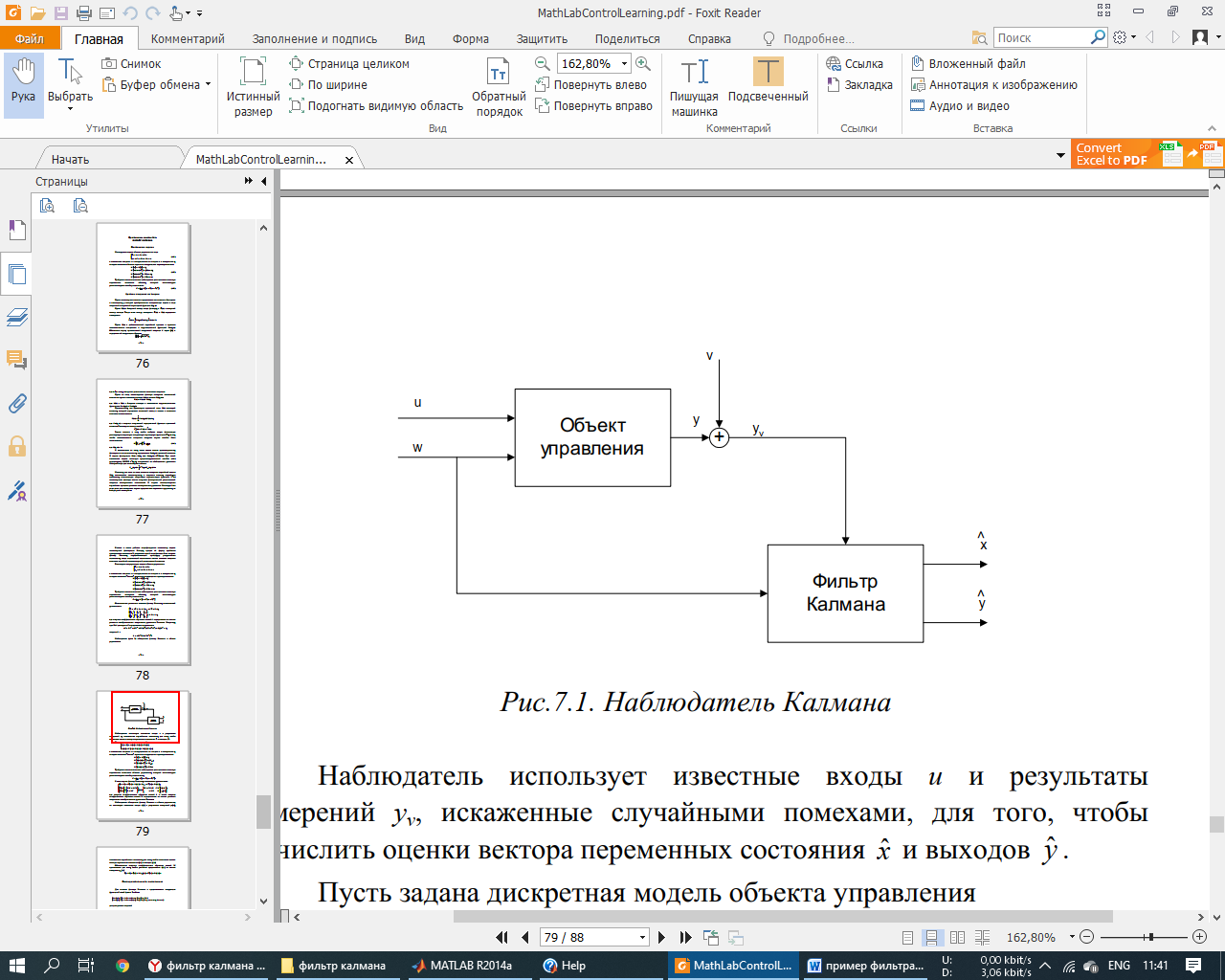 Рисунок 1 – Наблюдатель Калмана. Пример реализации фильтра Калмана. Фильтр реализован в файле fKalm.m. Пусть имеем объект с передаточной функцией 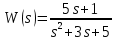 и параметрами шумов Q = 0,1; R = 0,01. Зададим систему управления в пространстве состояний %пример фильтра Калмана close all clear all %описание системы sys=ss(tf([5 1],[1 3 5])); [A,B,C,D]=ssdata(sys) %интенсивность шумов Q=0.1; R=0.01; %расчёт фильтра kest = kalman(sys,Q,R) %Расчёт выходов системы с наблюдателем %время t=0:0.001:5; %вход и шумы u=sin(pi*t/2); w=randn(size(t))*10*Q^0.5; v=randn(size(t))*R^0.5; %расчёт выхода системы u1=u+w; y1=lsim(sys, u1', t); %расчёт выхода фильтра uf=y1'+v+w; Af=kest.a Bf=kest.b Cf=kest.c(1,:) Df=0 FK=ss(Af, Bf, Cf, Df) yf = lsim(FK, uf, t); plot(t, yf,'-r',t,y1,'-b') Результат – командное окно и графики фильтрованного и нефильтрованного выхода. Графики показаны на рис.2. (При новом запуске графики могут отличаться из-за случайной составляющей). >> fKalm A = -3.0000 -2.5000 2.0000 0 B = 2 0 C = 2.5000 0.2500 D = 0 kest = a = x1_e x2_e x1_e -16.07 -3.807 x2_e 1.228 -0.07721 b = y1 x1_e 5.229 x2_e 0.3088 c = x1_e x2_e y1_e 2.5 0.25 x1_e 1 0 x2_e 0 1 d = y1 y1_e 0 x1_e 0 x2_e 0 Input groups: Name Channels Measurement 1 Output groups: Name Channels OutputEstimate 1 StateEstimate 2,3 Continuous-time state-space model. Af = -16.0731 -3.8073 1.2279 -0.0772 Bf = 5.2292 0.3088 Cf = 2.5000 0.2500 Df = 0 FK = a = x1 x2 x1 -16.07 -3.807 x2 1.228 -0.07721 b = u1 x1 5.229 x2 0.3088 c = x1 x2 y1 2.5 0.25 d = u1 y1 0 Continuous-time state-space model. 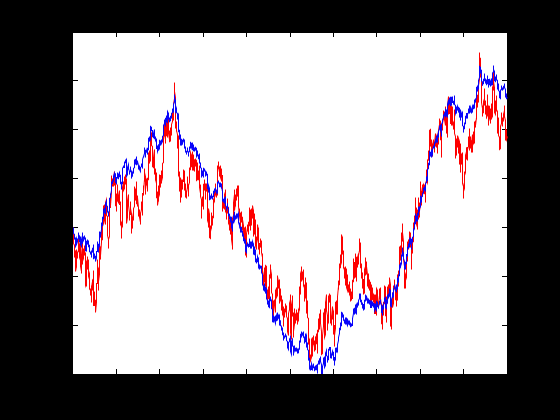 Рисунок 2 – Результат фильтрации (красный – зашумлённый сигнал, синий – отфильтрованный) |
