Изучение методики модального управления линейными динамическими объектами в пространстве состояний.. ЛБ_1_ТАУ. Цель работы Изучение методики модального управления линейными динамическими объектами в пространстве состояний. Исходные данные

• Название: Цель работы Изучение методики модального управления линейными динамическими объектами в пространстве состояний. Исходные данные
• Анкор: Изучение методики модального управления линейными динамическими объектами в пространстве состояний
• Дата: 10.04.2021
• Размер: 115.81 Kb.
• Имя файла: ЛБ_1_ТАУ.docx
• Тип: Документы; #193282

1. 
   Цель работы
   

Изучение методики модального управления линейными динамическими объектами в пространстве состояний.

2. 
   Исходные данные
   

Вариант 4

Исходными данными по варианту являются 3 матрицы A, B и C:

A

B

C

3. 
   Ход и выполнение работы
   

Для обоснования возможности модального управления воспользуемся критерием управляемости. Для этого в Matlab воспользуемся функцией ctrb для построения матрицы управляемости и вычислим ее детерминант. Система является управляемой, если детерминант не равен нулю.

Листинг программы поиска детерминанта:

A=[-60.8 -107 -34.7; 35 60 19; -10 -16.7 -5.3];

B=[0.228; -0.127; 0.038];

C=[35000 105000 140000];

MU=ctrb(A,B);

det(MU)

Результат выполнения программы:

ans = 0.0102

Определитель матрицы не равен нулю, следовательно, критерий управляемости выполняется.

С целью получения перерегулирования 0% необходимо опытным путём подобрать значения вектору желаемых полюсов P: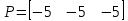

;

который задает желаемое расположение полюсов системы с помощью команды acker. Для получения масштабирующего коэффициента системы можно воспользоваться командой dcgain. Поделив единицу на установившееся значение системы можно получить масштабирующий коэффициент, позволяющий устранить установившуюся ошибку системы.

Для получения перерегулирования в 30%, необходимо задаться комплексными корнями, поскольку система имеет склонность к колебаниям, если характеристическое уравнение содержит комплексные корни η_1,2= –α ± jβ. Колебательность системы определяется по формуле: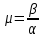

(1)

По значению колебательности можно оценить перерегулирование:
(2)

Необходимо, чтобы уровень перерегулирования составлял 30%. Следовательно, имеем: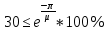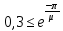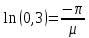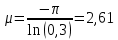









Таким образом, примем вектор, задающий желаемое расположение полюсов P при перерегулировании 30%: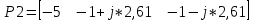

4. 
   Результаты работы
   

Код в MATLAB:

A=[-60.8 -107 -34.7; 35 60 19; -10 -16.7 -5.3];

B=[0.228; -0.127; 0.038];

C=[35000 105000 140000];

MU=ctrb(A,B);

det(MU);

P=[-5 -5 -5];

k=acker(A,B,P);

yust=dcgain(ss(A-B*k,B,C,0));

km1=1/yust
km1 =
0.0042

// Выполняем запуск модели в Matlab Simulink, получаем график для 0% перерегулирования; используем Gain «km1»

>> P2=[-5 -1+j*2.61 -1-j*2.61];

k=acker(A,B,P2);

yust=dcgain(ss(A-B*k,B,C,0));

km2=1/yust
km2 =
0.0013

// Выполняем запуск модели в Matlab Simulink, получаем график для 30% перерегулирования; используем Gain «km2»

На рисунке 1 изображена система с обратной связью, построенная в пакете Matlab Simulink.


б)

a)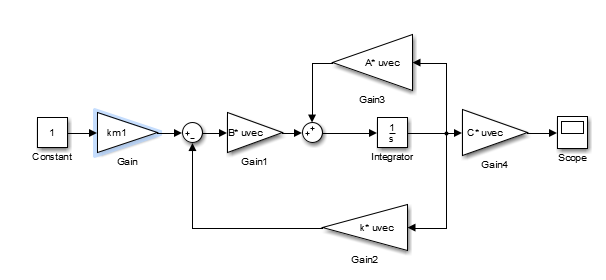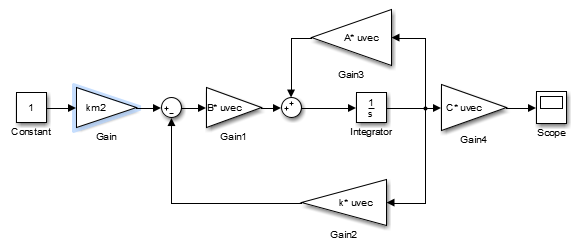


Рис.1 – Система с обратной связью, построенная в пакете Matlab Simulink а) с перерегулированием 0%; б) с перерегулированием 30%
На рисунках 2 и 3 изображены графики переходных процессов с нулевым перерегулированием, и перерегулированием 30% соответственно.


Рис. 2 – График переходного процесса с нулевым перерегулированием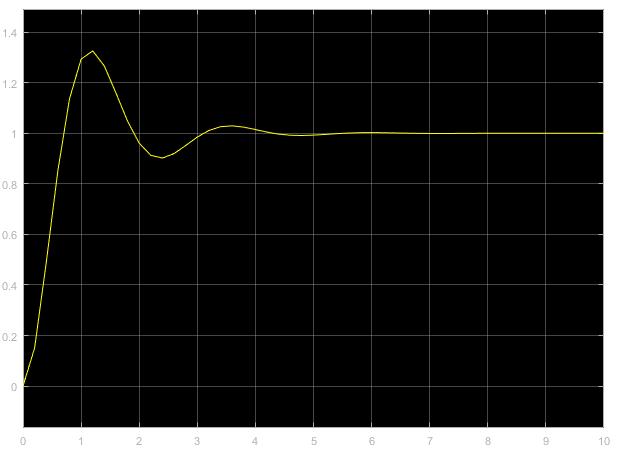

Рис. 3 – График переходного процесса с перерегулированием 30%

5. 
   Выводы
   

В ходе выполнения лабораторной работы были изучены методики модального управления линейными динамическими объектами в пространстве состояний. Были приобретены навыки в построении системы с заданным уровнем перерегулирования.