контрольная (вариант 7) старая контрольная. Контрольная работа Вариант 7 Содержание Задание 1 3 Задание 2 5 Задание 3 7 Задание 4 9 Список литературы 11
 Скачать 49.12 Kb. Скачать 49.12 Kb.
|
|
Автоматизация процессов измерений, испытаний и контроля Контрольная работа Вариант 7 Содержание Задание 1 3 Задание 2 5 Задание 3 7 Задание 4 9 Список литературы 11 Задание 1Исследовать стабилизируемость системы с уравнением состояния: 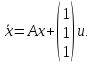 Таблица 1
Решение В соответствии с данными варианта перепишем уравнение состояния: 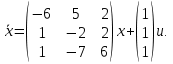 Проверяем условие невырожденности: 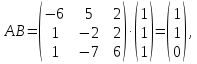 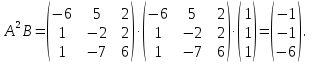 Т.е. получаем блочную матрицу: 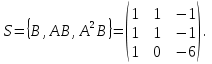 Ранг этой матрицы равен 2. Система не является полностью управляемой. Приведем уравнение состояния к канонической форме управляемости: 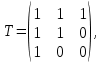 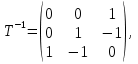 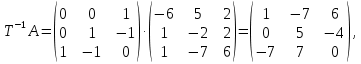 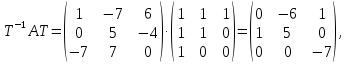 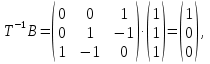 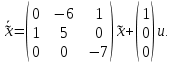 Неуправляемая часть системы 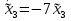 асимптотически устойчива. Система стабилизируема. асимптотически устойчива. Система стабилизируема.Задание 2Для системы: 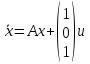 построить стабилизирующее управление, обеспечивающее управляемой части собственное число 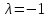 . .Таблица 2
Решение В соответствии с данными варианта перепишем уравнение состояния: 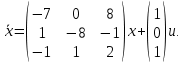 Проверяем условие невырожденности: 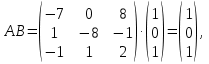 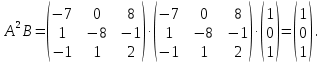 Т.е. получаем блочную матрицу: 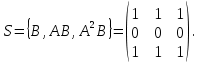 Ранг этой матрицы равен 1, т.е. 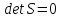 . Система является полностью неуправляемой. . Система является полностью неуправляемой.Следовательно, построить стабилизирующее управление, обеспечивающее управляемой части собственное число 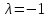 не представляется возможным. не представляется возможным.Задание 3Исследовать обнаруживаемость системы с уравнениями движения: 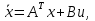 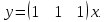 Значения матрицы 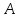 приведено в таблице 1. приведено в таблице 1.Решение В соответствии с данными условия варианта перепишем систему: 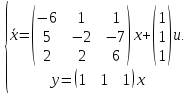 Вычислим строки матрицы наблюдаемости 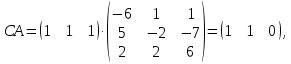 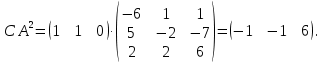 Матрица наблюдаемости 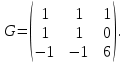 имеет ранг 2. Её первые две строки линейно независимы. Строим матрицу: 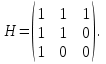 выбрав третью строку произвольно, но так, чтобы 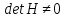 . .Выполним замену 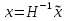 . .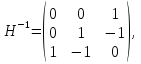 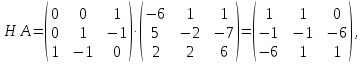 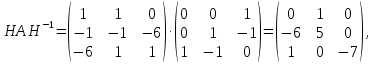 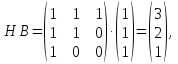 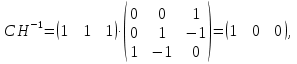 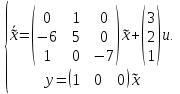 Координаты 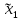 , , 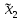 наблюдаемы, наблюдаемы, 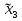 – ненаблюдаема. – ненаблюдаема.Система является обнаруживаемой. Задание 4Построить наблюдатель полного порядка для линейной стационарной системы: 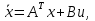 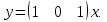 Значения матрицы 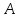 приведено в таблице 2. приведено в таблице 2.Решение В соответствии с данными условия варианта перепишем систему: 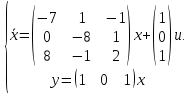 Вычислим собственные значения матрицы 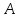 : :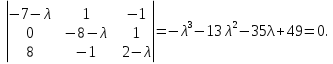 Находим корни уравнения: 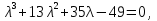 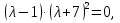 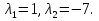 Обозначим элементы матрицы 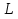 через через 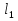 , , 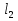 и и 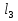 . .Тогда 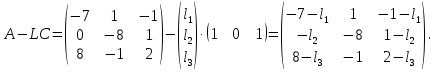 Найдем характеристический полином матрицы 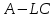 : :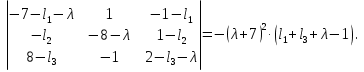 Сравнение коэффициентов полинома 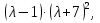 и характеристического полинома матрицы и характеристического полинома матрицы 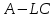 дает: дает: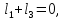 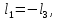 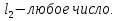 Т.е. получаем множество наблюдателей полного порядка вида: 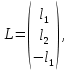 Для примера можно записать один из возможных вариантов с численными значениями: 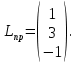 Список литературы1. Автоматизация процессов измерений, испытаний и контроля. Конспект лекций. 2. Коршунов Ю.М. Математические основы кибернетики: Учеб, пособие. – М.: Энергоатомиздат, 1987. 3. Кузовков Н.Т. Модальное управление и наблюдающие устройства. – М:. Наука, 1976. |
